Important Theorems and Rules of Triangle
Pythagoras Theorem
In a right-angled triangle, the square of the hypotenuse is equal to sum of the squares of the other two sides.
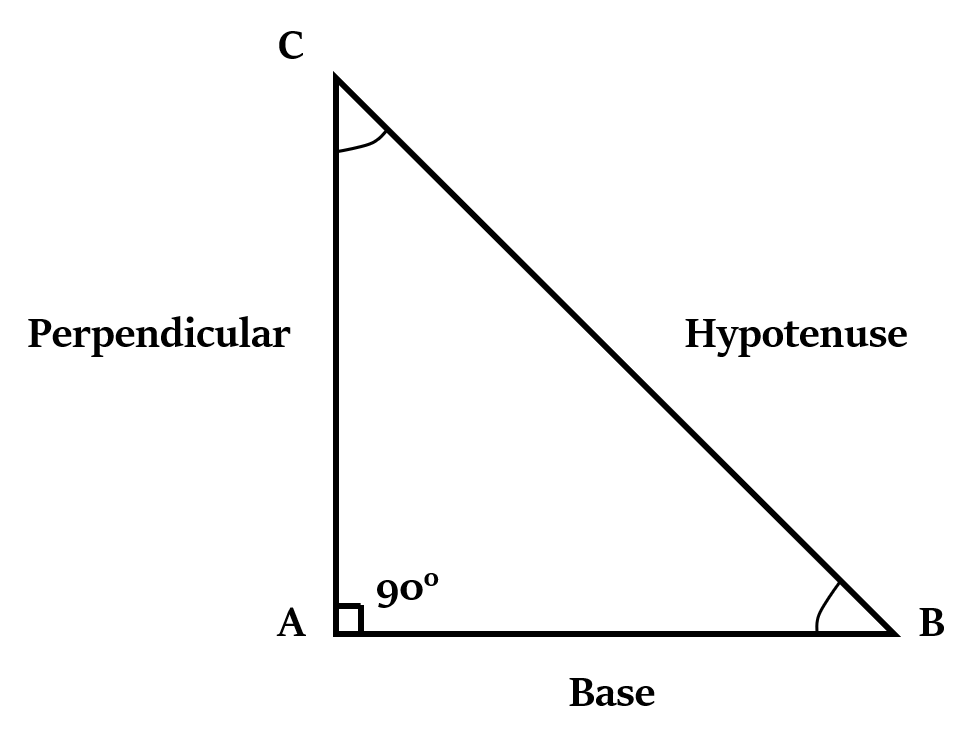
or
We can remember some very common Pythagorean Triplets. You will encounter these pretty frequently.
(3, 4, 5), (5, 12, 13), (6, 8, 10), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (30, 40, 50)
We can also apply this theorem to other types of triangles with some variation.
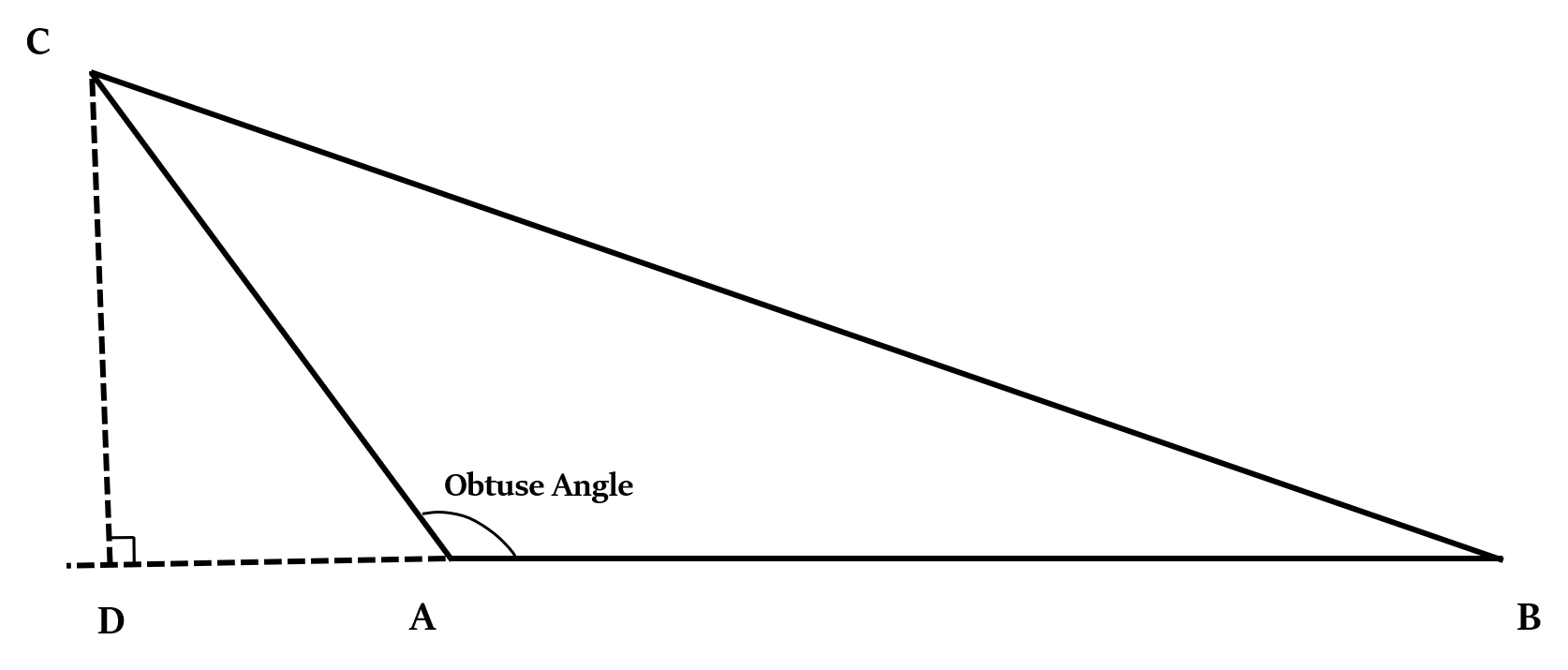
In Obtuse angled triangle:
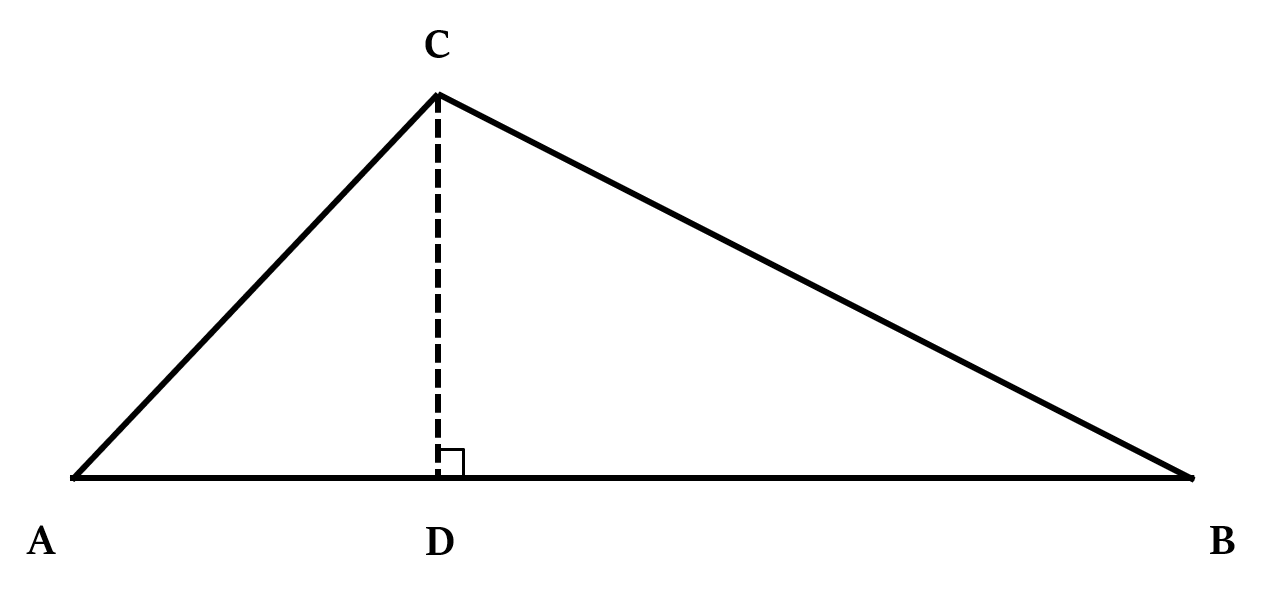
In Acute angled triangle:
Median related Theorems
Theorem 1
In ∆ABC, if CD is the median, then:
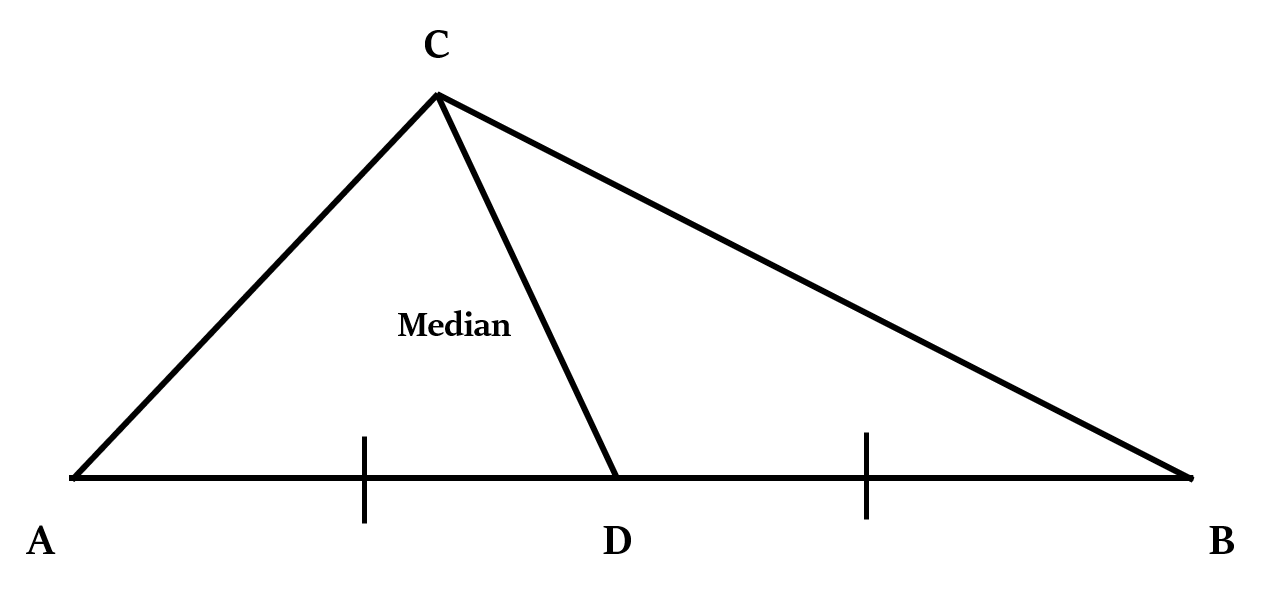
Now, as AD = BD. So, we can also write it as:
Theorem 2
In ∆ABC, if AD, BE, CF are the medians, then:
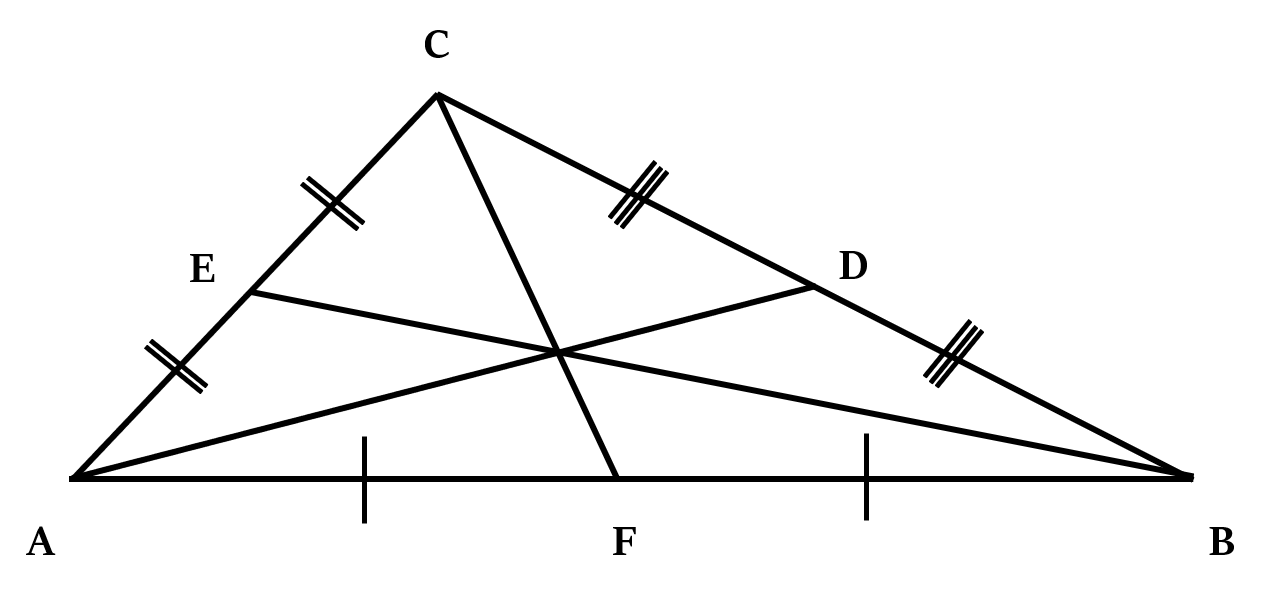
Theorem 3
In right-angled ∆ABC, if BE and CF are the medians drawn from the acute angles, then:
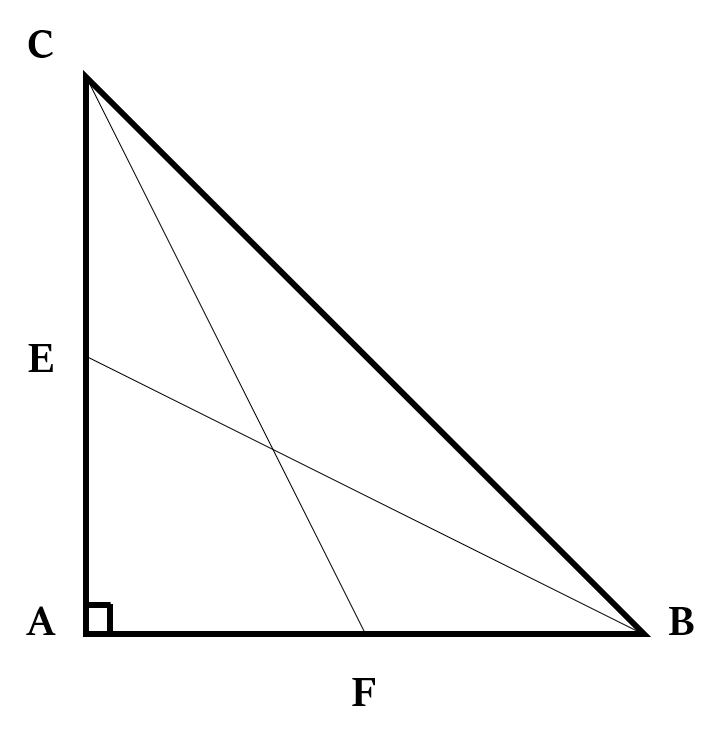
That is, four times the sum of the square of the medians drawn from the acute angles is equal to five times the square of the hypotenuse (only in case of right-angled triangle).
Sine Rule
Sine rule, or the law of sine is pretty useful in finding the sides and angles of any triangle.
In ∆ABC, if a, b and c are the sides and A, B and C are the angles opposite to them respectively, then:
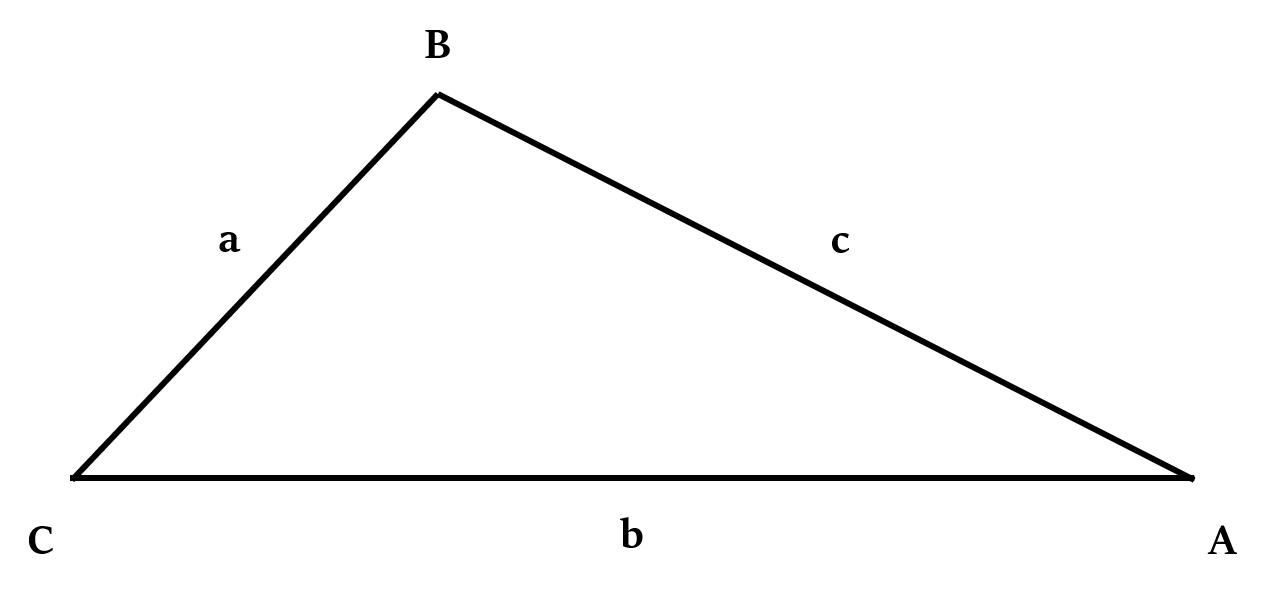
We use this formula, when:
- two sides and an angle opposite to one of them are given.
- two angles and a side opposite to one of them are given.
Cosine Rule
Cosine rule, or the law of cosine is pretty useful in finding the sides and angles of any triangle.
In ∆ABC, if a, b and c are the sides and A, B and C are the angles opposite to them respectively, then:

We use this formula, when:
- three sides are given.
- two sides and the angle in between those two sides are given.
Mass Point Geometry Theorem
Centre of mass of an object is the point at which the object can be balanced.
If there are masses
x =
Crossed Ladders Theorem
If AB ‖ EF ‖ CD and AD & BC intersect at E, then:
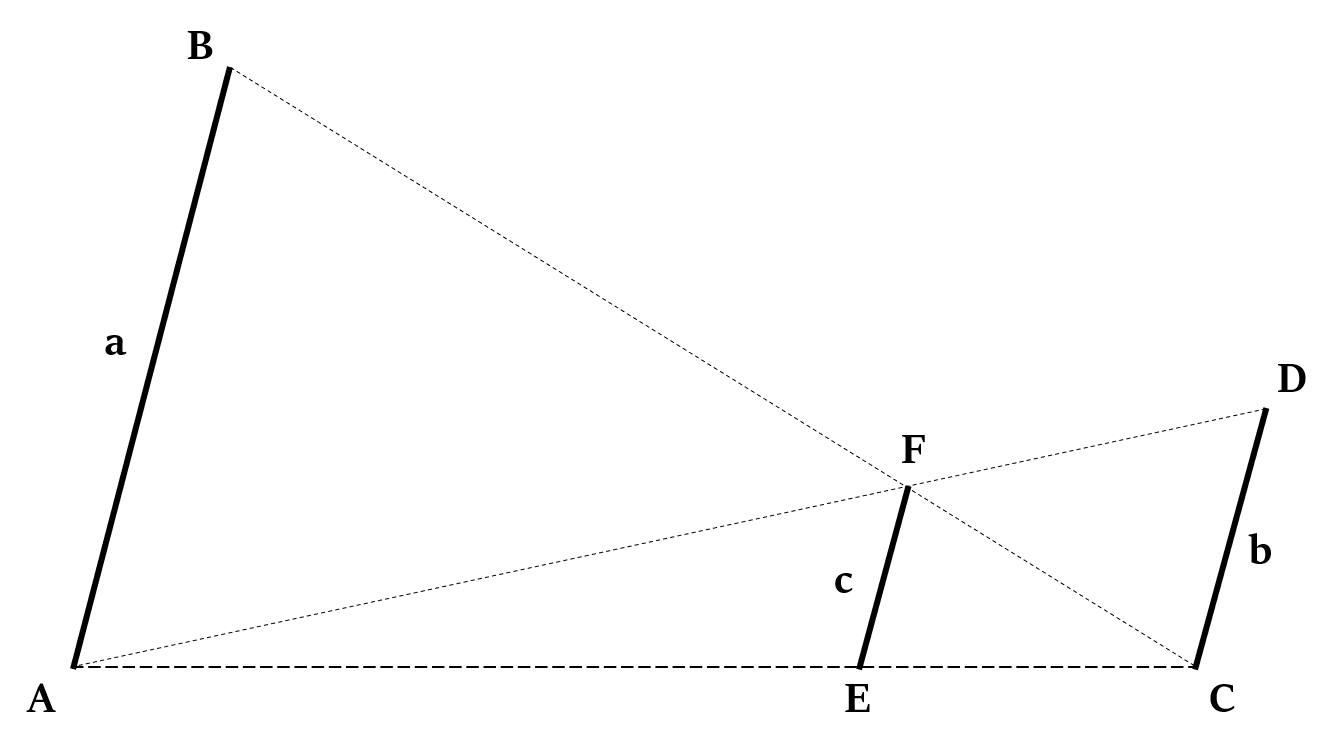
or c =
Now, let’s see some other theorems based on Crossed Ladders Theorem.
Theorem 1
In ∆ABC, if:
- D lies on the side AC, E lies on the side BC, and AE & BD intersect at M
- DD’, CC’, MM’ and EE’ are parallel, then:
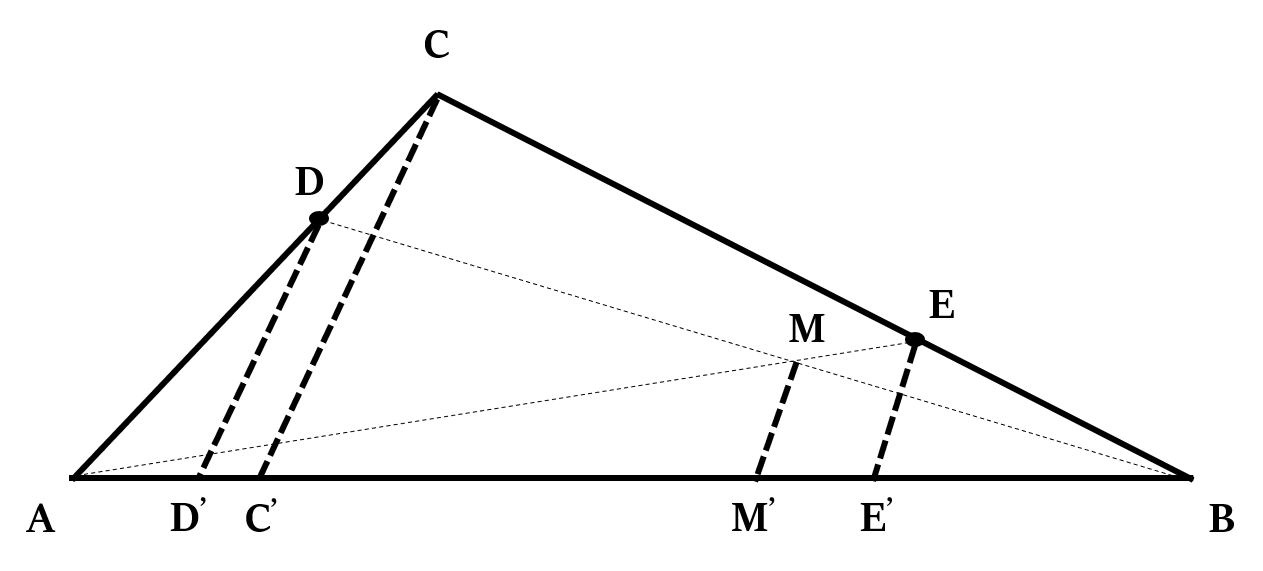
Theorem 2
We can also use Crossed Ladders Theorem to find the area of a triangle.
In ∆ABC, if:
- D lies on the side AC, E lies on the side BC, and AE & BD intersect at M
- w is the area of the ∆ABC, and x, y, z are the areas of the smaller triangles as shown in the following figure, then:
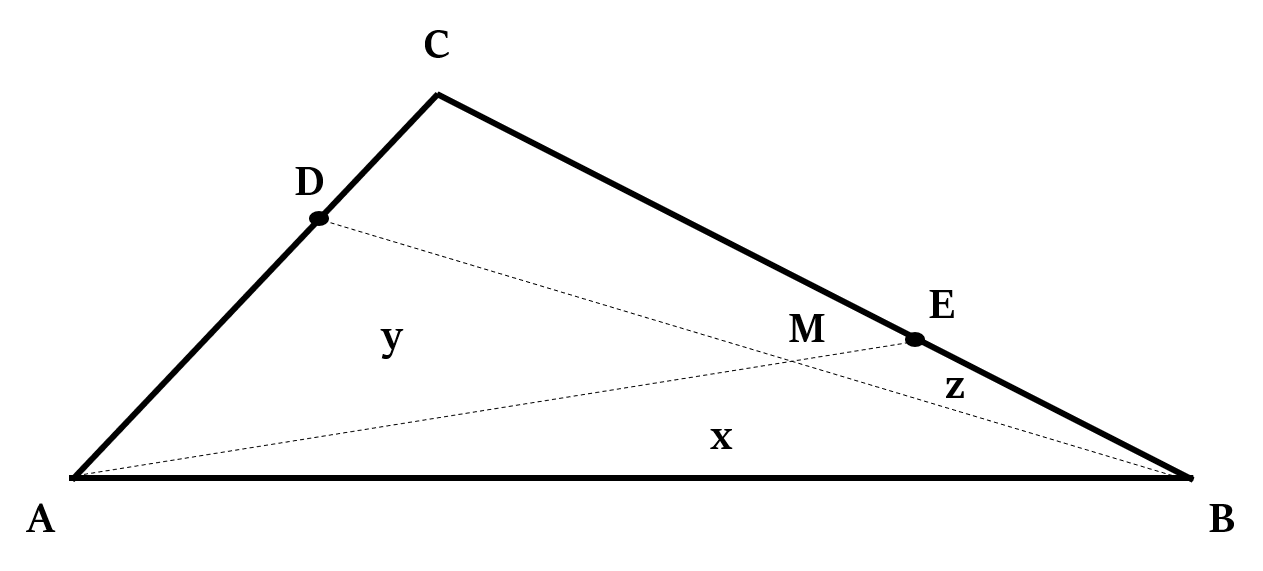
Theorem 3
We can also apply Crossed Ladders Theorem in case of trapezium (a quadrilateral with one pair of sides parallel).
If ABCD is a trapezium, such that:
- length of its parallel sides are a and b units respectively
- EF is a line parallel to the trapezium’s parallel sides, such that it divides the trapezium’s non-parallel sides in the ratio m:n, then:
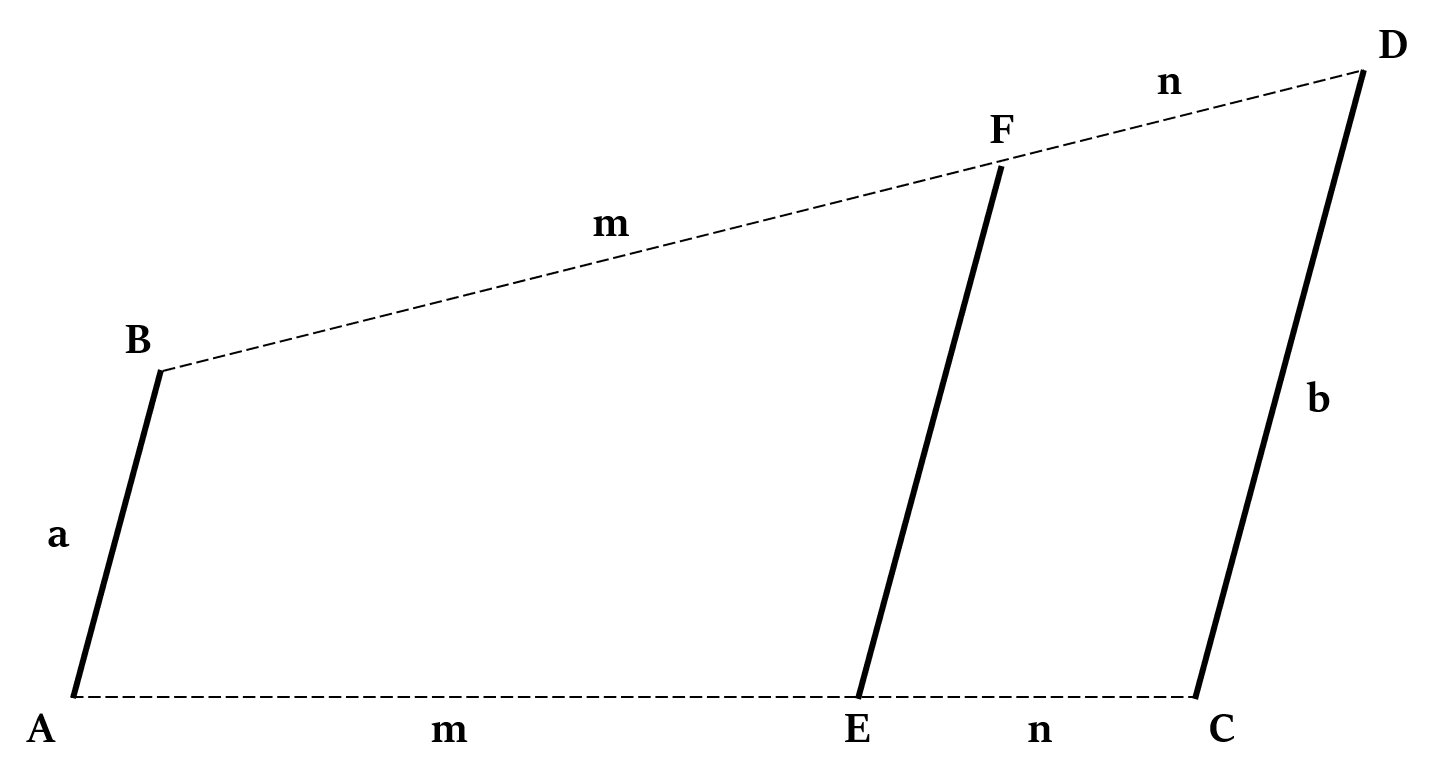
Length of EF = a + m
Some more Theorems
Theorem 1
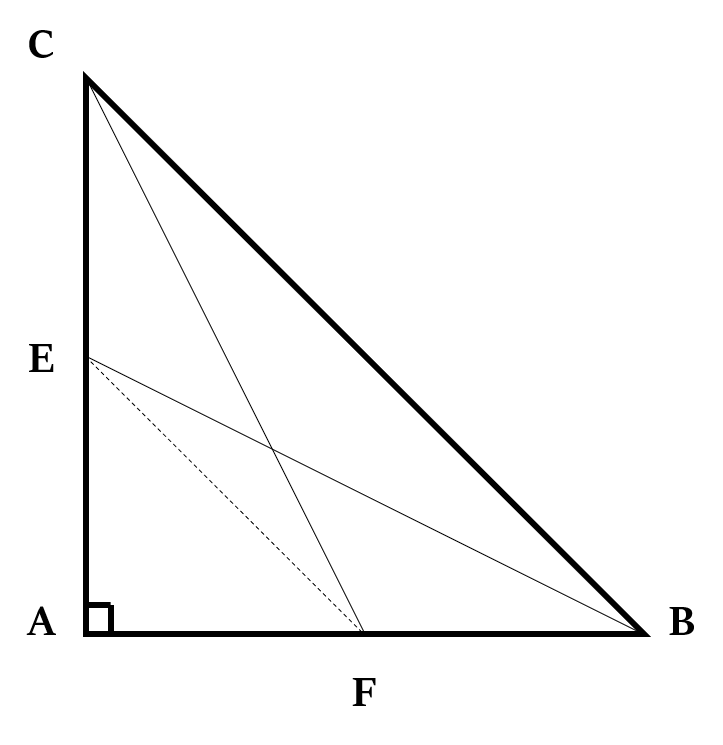
In right-angled ∆ABC, if E and F are any points on perpendicular and base, then: