Area of Quadrilaterals
Let us see the various formulae that we can use:
- to find area of any general quadrilateral
- to find area of some specific kind of a quadrilateral, e.g. trapezium, rhombus etc.
Formulae for Area of Quadrilateral
Formula 1
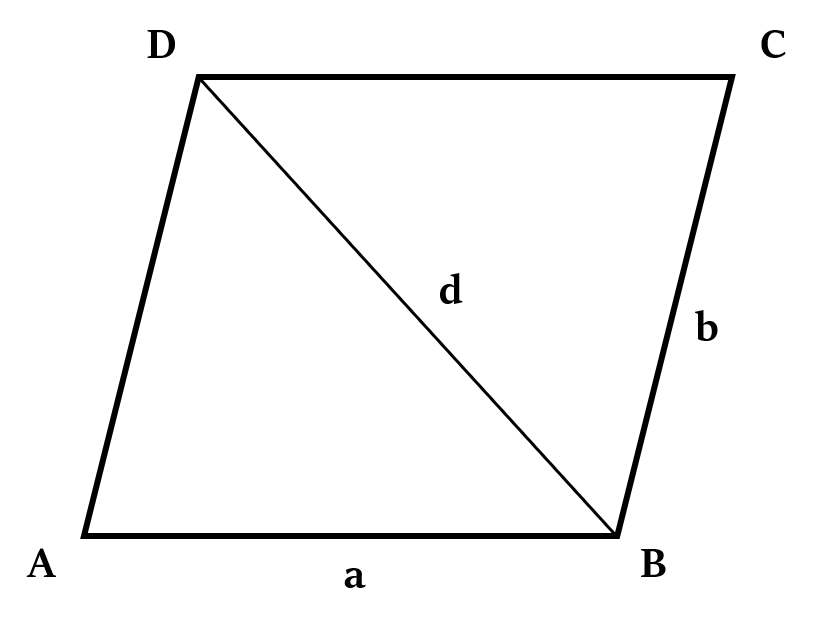
Area of Quadrilateral = 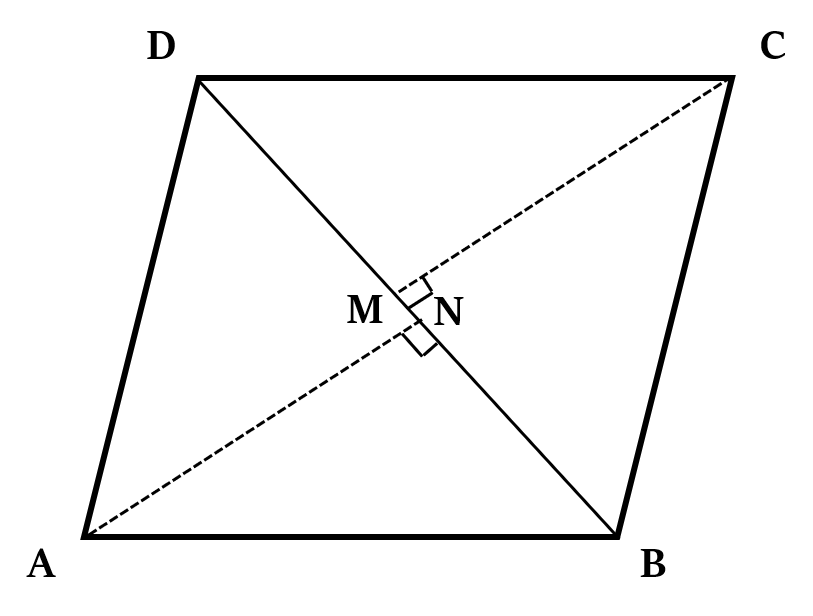 Area of □ABCD =
Area of □ABCD =
Basically its akin to adding the areas of two triangles, ABD and CDB.
Formula 2
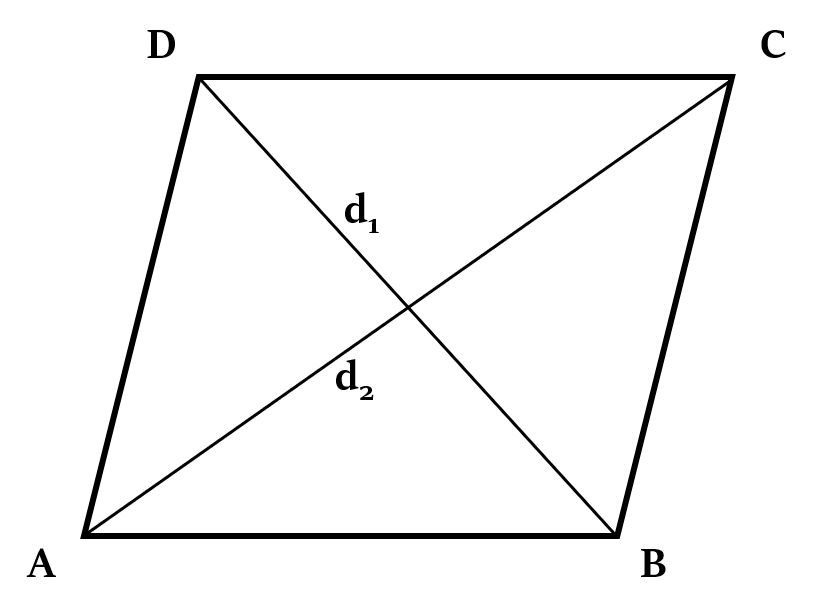
Area of quadrilateral = 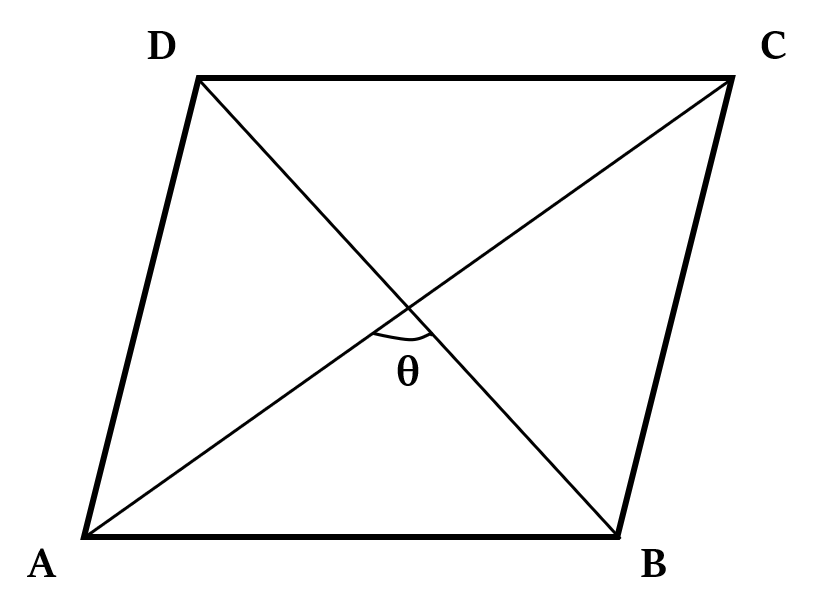 Area of □ABCD =
Area of □ABCD =
Formulae for Area of Cyclic Quadrilaterals
If the length of the sides of the cyclic quadrilateral are a, b, c and d, then:

Area of cyclic quadrilateral =
Where, s =
Formulae for Area of Parallelograms
Here are a few formulae that we can use for any kind of a parallelogram.
Formula 1
Area of parallelogram = Base × Height
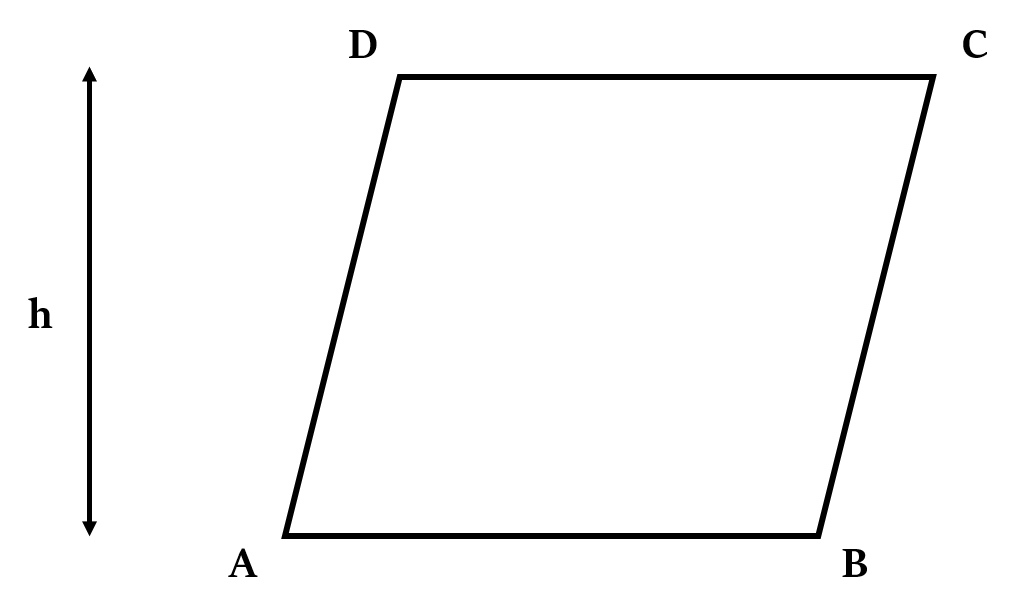
In the above figure, Area of parallelogram = AB × h
If the angle between the base and another side of length ‘a’ is θ, then:
height (h) = a sin θ
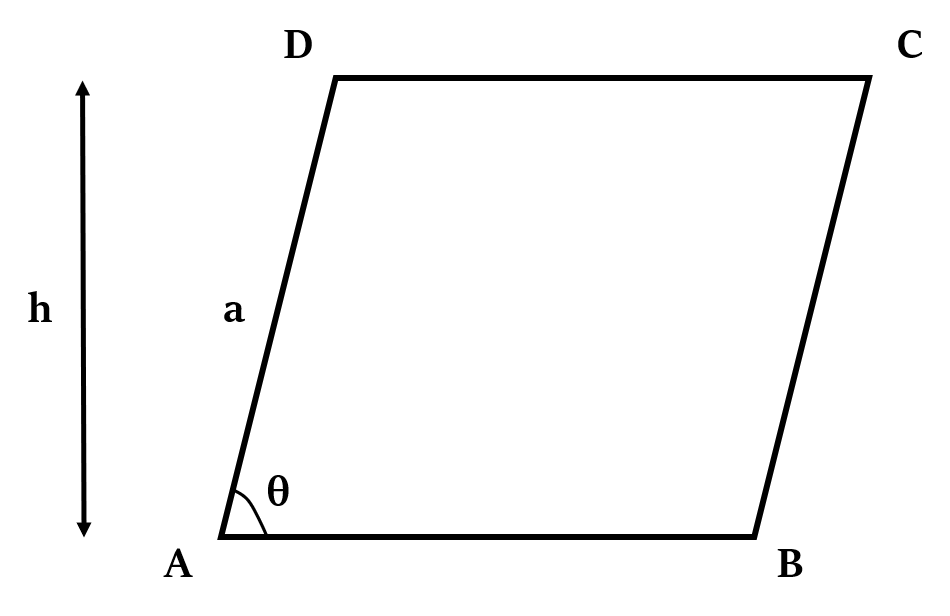
Area of parallelogram = AB × h = AB × a sin θ
Formula 2
If the length of two adjacent sides of a parallelogram are a and b, and length of any one of the diagonals is d, then:
Area of parallelogram = 2
Where, s =
However, there are a few formulae that we can use for some specific kinds of parallelograms. Let’s see these too.
Formula 3: For Rhombus
If the given parallelogram is a rhombus, the we can also use the following formula to find its area.
Area of Rhombus =
We use the same formula for finding the area of a kite too.
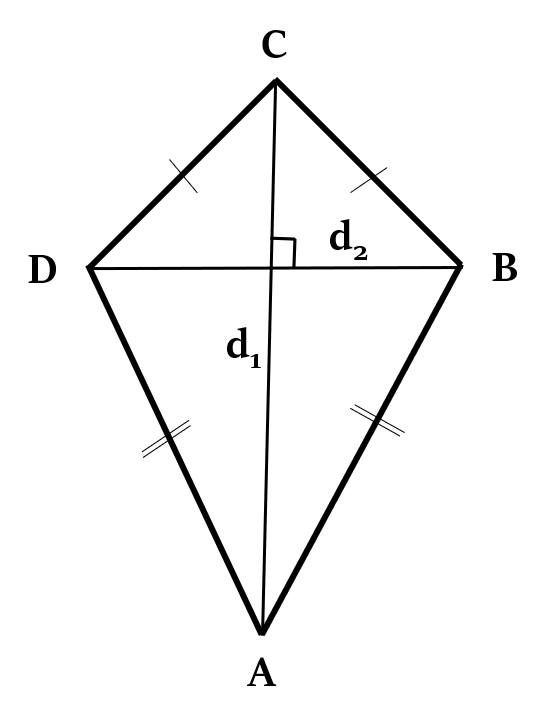
Area of Kite =
Formula 4: For Square
If the given parallelogram is a square, then we can also use the following formula to find its area.
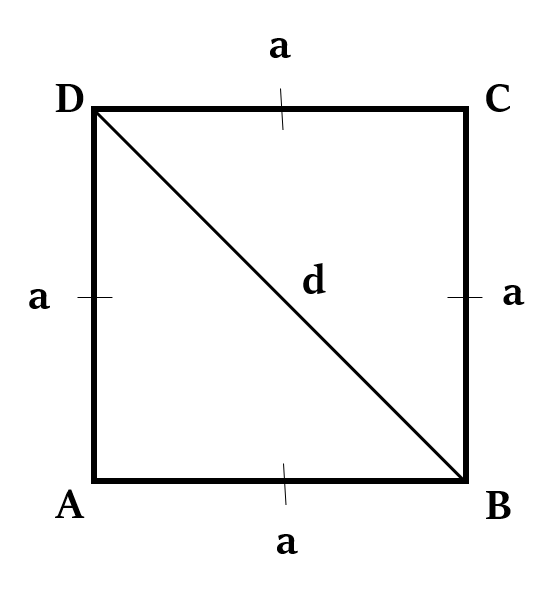
Area of Square =
Formula 5: For Circumscribed Square
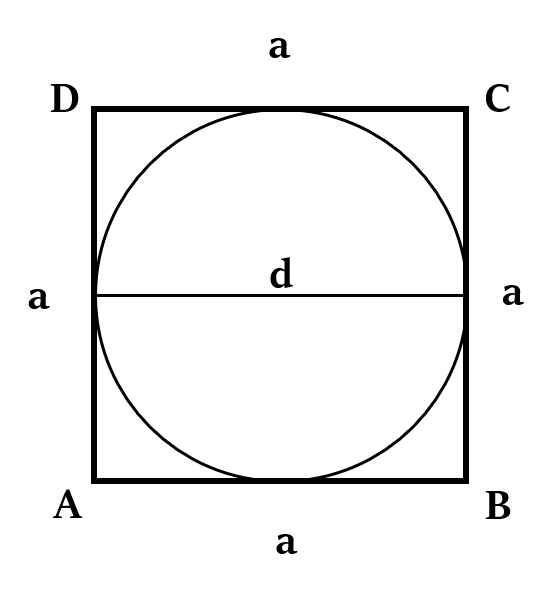
Side of circumscribed square, a = Diameter of the inscribed circle, d
Ratio of area of inscribed circle and area of circumscribed square =
Formula 6: For Rectangle
Formula 6a
If the given parallelogram is a rectangle, then we can also use the following formula to find its area.
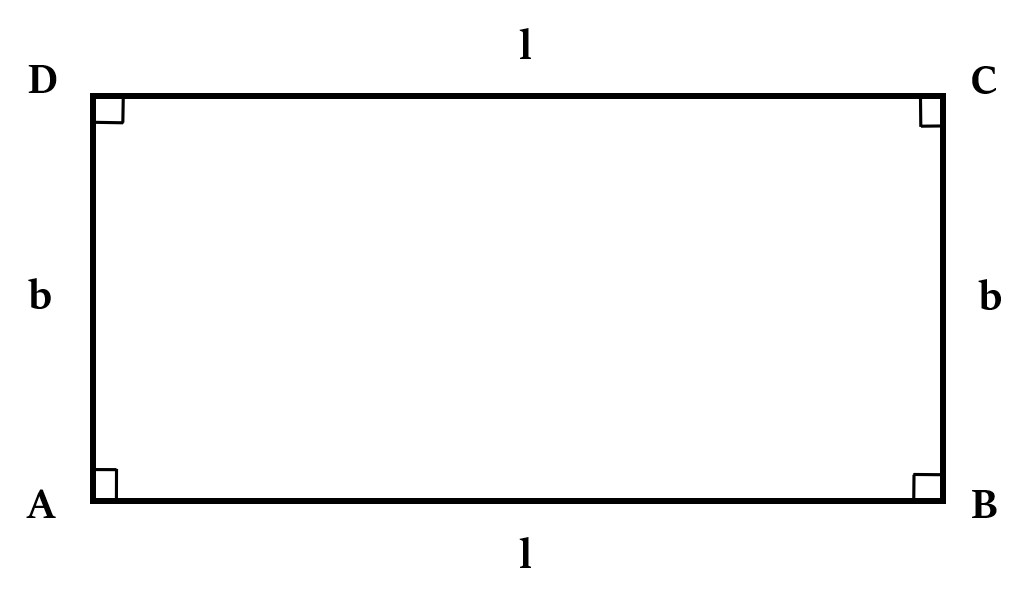
Area of rectangle = Length x Breadth = l x b
Formula 6b: Pathway across the middle of a rectangle
Have a look at the pathway across the middle of a rectangle.
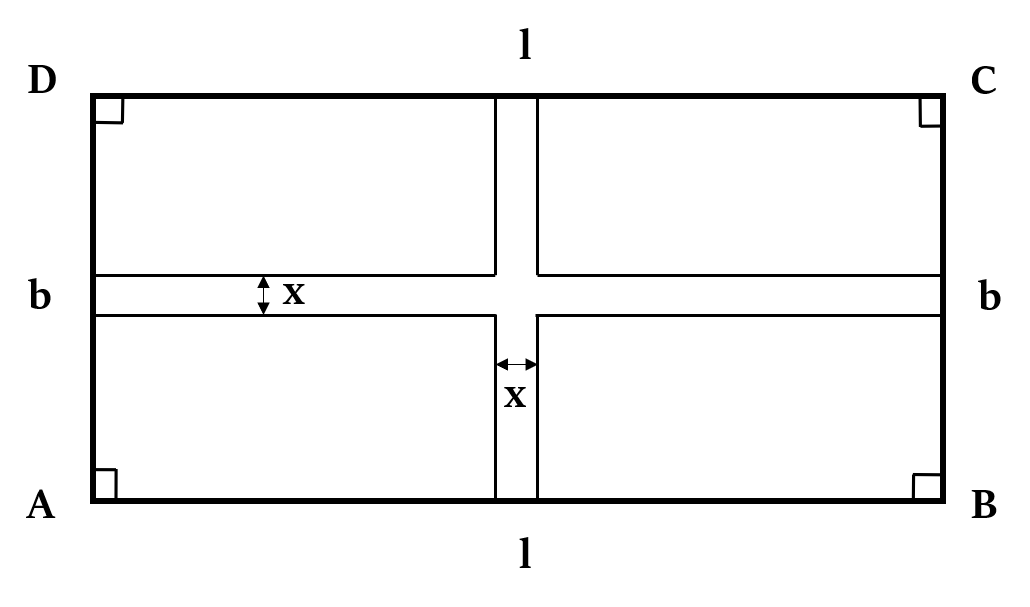 Area of path = (l + b – x)x
Area of path = (l + b – x)x
Perimeter of path = 2(l + b) – 4x = 2(l + b – 2x)
Formula 6c: Pathway around a rectangle
Have a look at the pathway around a rectangle (pathway is inside the rectangle).
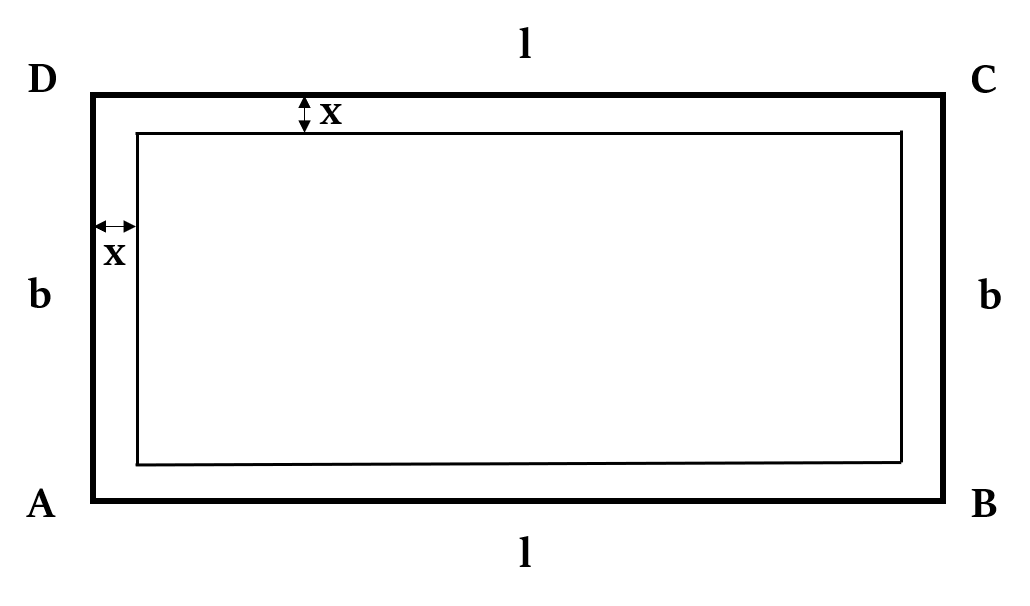 Area of the path = (l + b – 2x)2x
Area of the path = (l + b – 2x)2x
Primeter = Inner perimeter + Outer perimeter = 2(l + b - 4x) + 2(l + b) = 4 (l + b – 2x)
Have a look at the pathway around a rectangle (pathway is outside the rectangle).
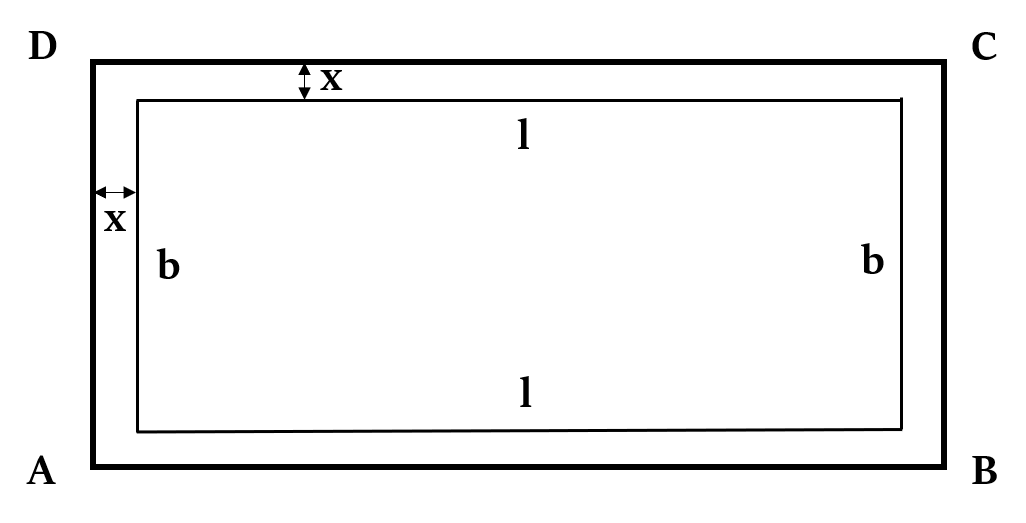 Area = (l + b + 2x)2x
Area = (l + b + 2x)2x
Perimeter = Inner perimeter + Outer perimeter = 2 (l + b) + 2(l + b + 4x) = 4(l + b + 2x)
Formulae for Area of Trapezium
Area of trapezium = 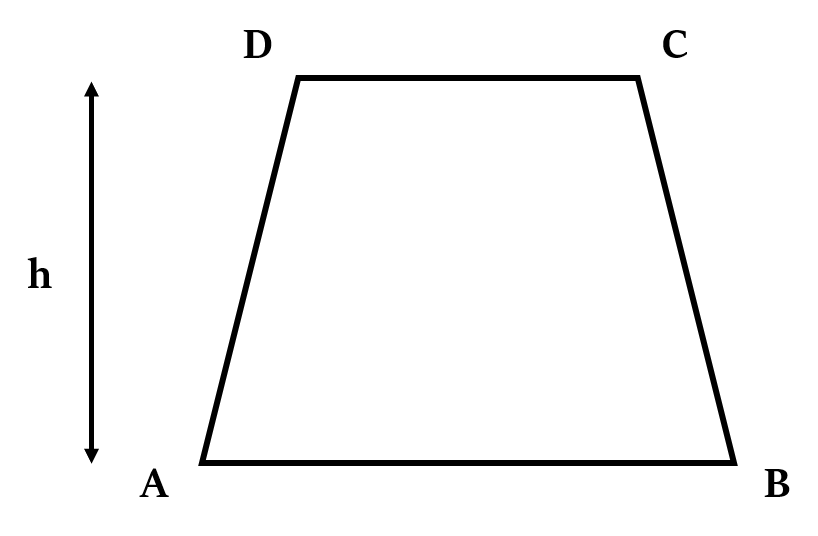
In the above figure, Area of trapezium =
Properties related to Area of a Quadrilateral
Property 1
If two parallelograms have the same base (or same base length), and are between the same parallel lines (i.e. their height is the same), then their area will be equal.
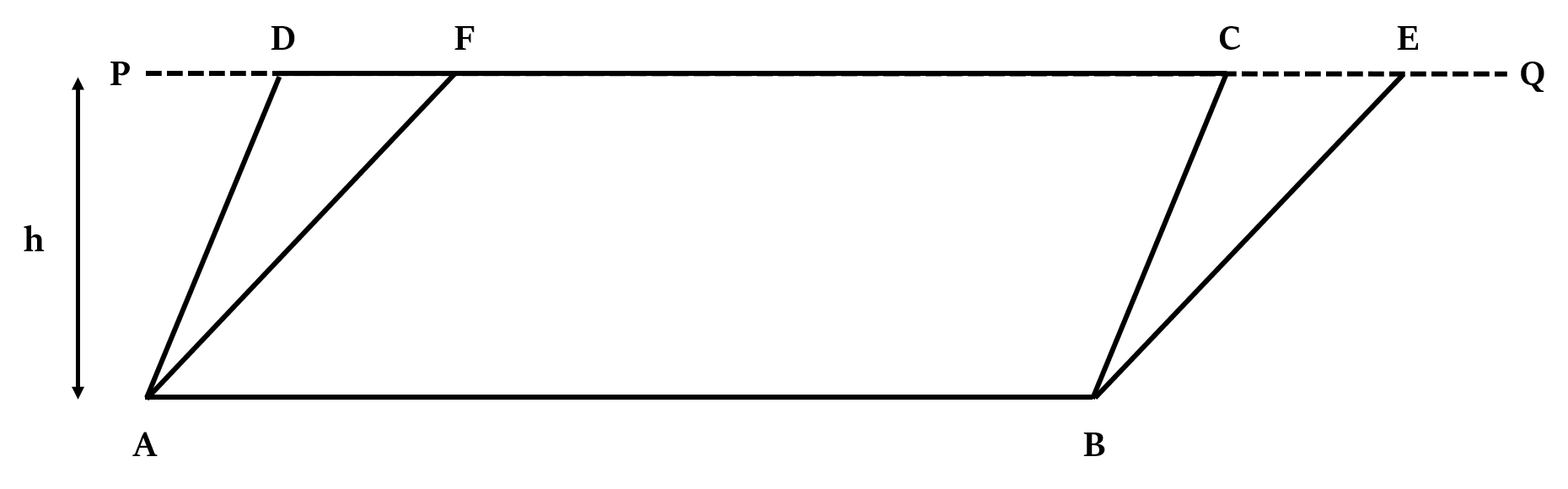 If AB ∥ PQ, then, Area of □ABCD = Area of □ABEF
If AB ∥ PQ, then, Area of □ABCD = Area of □ABEF
This is because area of a parallelogram is equal to the product of its base and height. If heights of two parallelograms are the same and the length of their bases too (as is the case above), then they obviously will have the same area.
Property 2
If the side/diagonal of a square becomes x times, then the area of the square will become
Property 3
In case of a rectangle (or a square), if its length is increased by x%, then in order to maintain the same area of the rectangle its breadth will have to be decreased by
Property 4
If all the sides of a quadrilateral are increased (or decreased) by x%, then its diagonals are also increased (or decreased) by x%.
If all of the sides of any 2-D figure are increased (or decreased) by x%, then:
- its perimeter also increases (or decreases) by x%.
- its area changes by