Circle Theorems

In this article, we will have a look at the various properties and theorems related to circles.

If ‘r’ is the radius of a circle, then:

Area of Circle

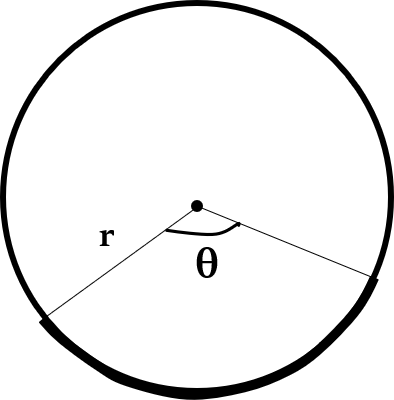Area of circle = π$r^2$ Geometry

Area of sector which subtends an angle θ at the centre = $\frac{θ}{360°}$ × π$r^2$ Geometry

θ is in degrees.

Ring is the space enclosed between two concentric circles. 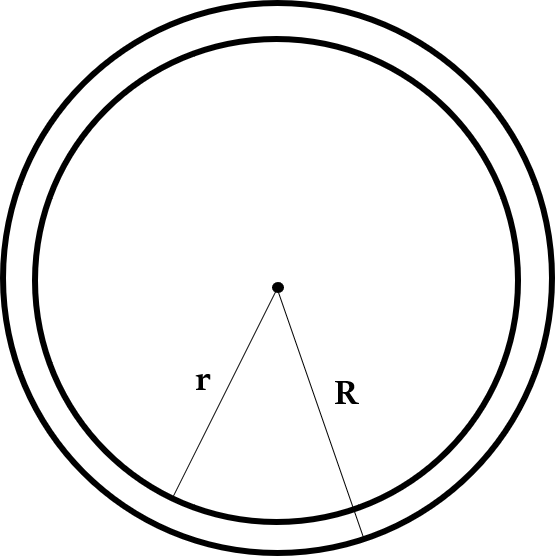Geometry Area of ring = Area of bigger circle - Area of smaller circle = π$R^2$ - π$r^2$ = π$(R^2 - r^2)$

Circumference of Circle

Circumference of circle = 2πr

Length of arc which subtends an angle θ at the centre = $\frac{θ}{360°}$ × 2πr Geometry

θ is in degrees.

Ring is the space enclosed between two concentric circles. Geometry Perimeter of ring = Perimeter of bigger circle + Perimeter of smaller circle = 2πR + 2πr = 2π (R + r)

Property 1

One and only one circle passes through any three given non-collinear points.

Property 2: Equal chords

Property 2a

Equal chords of a circle subtend equal angles at the centre. 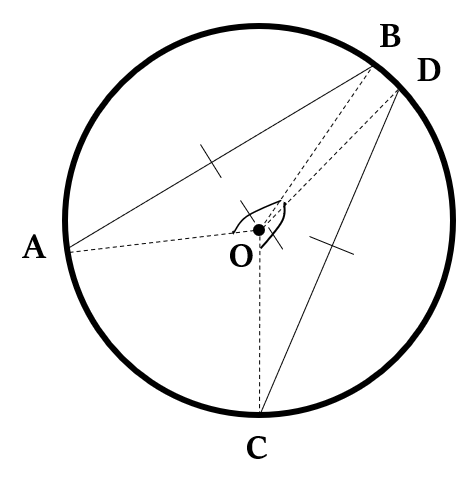Geometry In the figure given above, chords AB and CD are equal, i.e. AB = CD
So, ∠AOB = ∠COD

In other words, if the angles subtended by two chords of a circle at the centre are equal, then those two chords must be equal.

If two chords of a circle are equal, then their corresponding arcs are equal (i.e. congruent) too. Conversely, if two arcs are equal (i.e. congruent), then their corresponding chords are equal.

So, in short, equal arcs or equal chords of a circle subtend equal angles at the centre.

Property 2b

Equal chords of a circle (or of congruent circles) are equidistant from the centre. 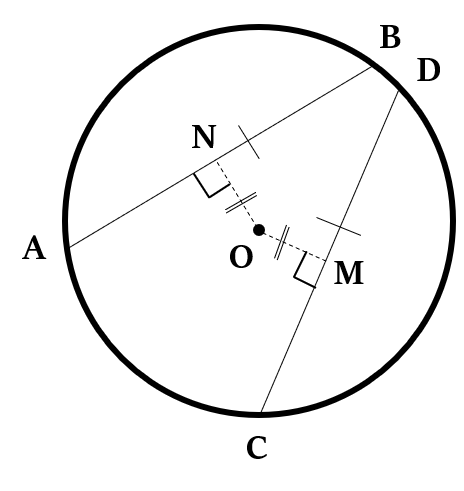Geometry In the figure given above, chords AB and CD are equal, i.e. AB = CD
So, OM = ON

In other words, chords equidistant from the centre of a circle are equal in length.

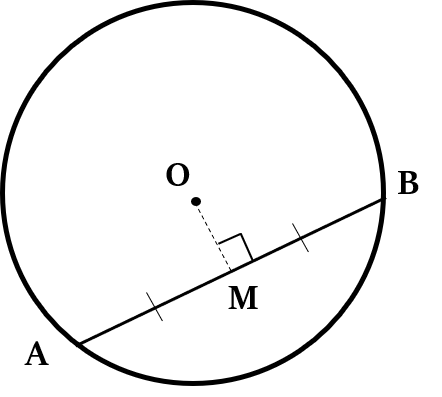
Property 3

The perpendicular from the centre of a circle to a chord bisects that chord. Geometry

In other words, a line drawn through the centre of a circle to bisect a chord is perpendicular to that chord.

Property 4: Tangent

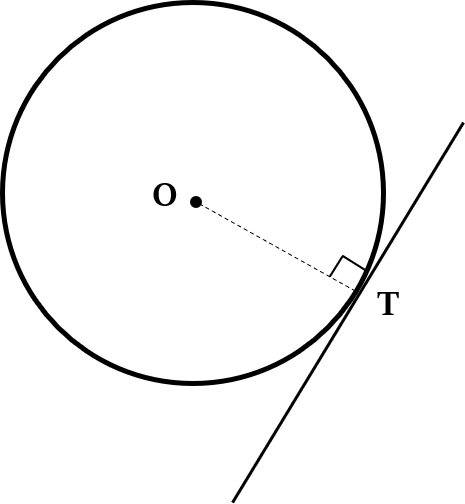
Property 4a

The tangent at any point of a circle is perpendicular to the radius through their point of contact. Geometry

Property 4b

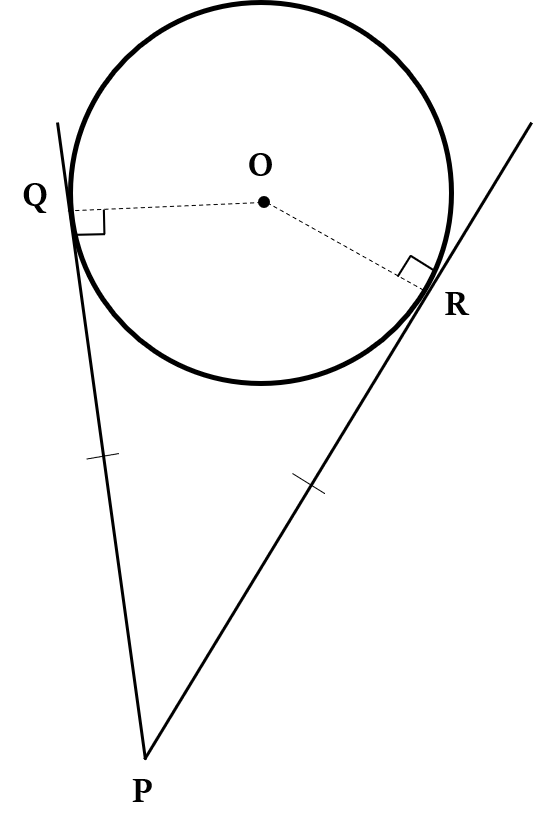
The lengths of tangents drawn from an external point to a circle are equal. Geometry

In the above figure, PR = PQ

Property 4c

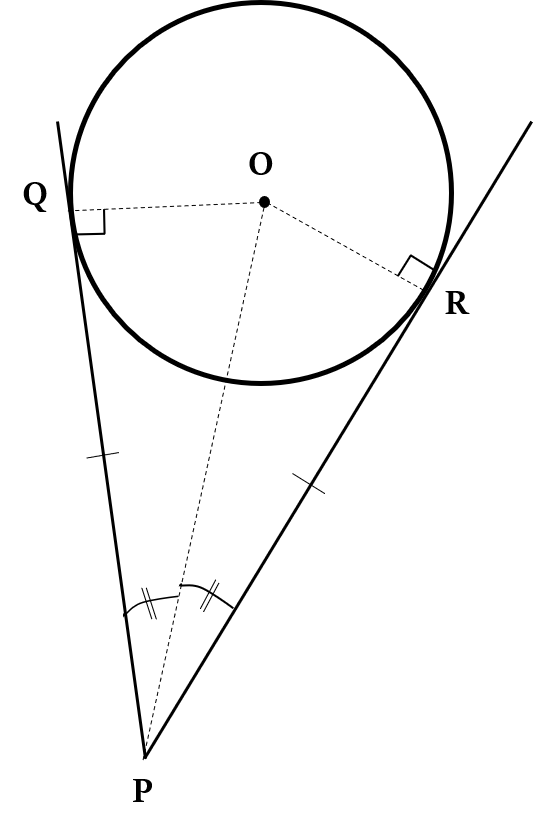
The angle formed by two tangents meeting at an external point is bisected by a straight line joining the centre of the circle to that external point. Geometry

In the above figure, PO bisects the ∠QPR, i.e. ∠QPO = ∠RPO
Also, as two angles of the triangles ∆PQO and ∆PRO are equal, their third angles must be equal too, i.e. ∠POQ = ∠POR.

Property 4d

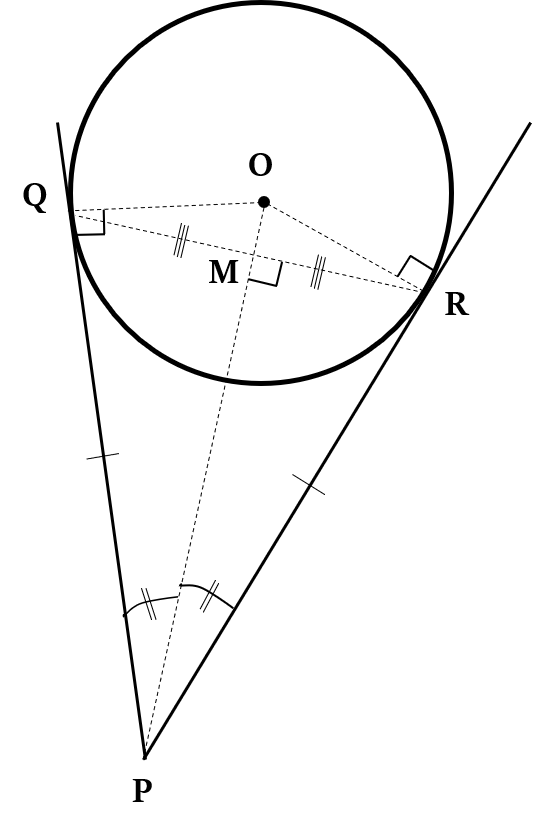
The chord formed by joining the point of contacts of two tangents (of a circle) from an external point is bisected perpendicularly by a straight line joining the centre of the circle to that external point. Geometry

In the above figure, QR is the chord formed by joining the points of contact of two tangents from point P.
So, chord QR is bisected perpendicularly by the line PO, i.e. QM = RM, and PO ⟂ QR.

Property 5

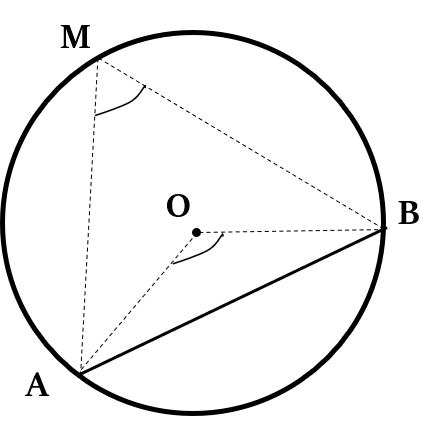
The angle subtended by an arc (or a chord) at the centre is double the angle subtended by it at any point on the remaining part of the circle. Geometry

In the above figure, ∠AOB = 2 ∠AMB

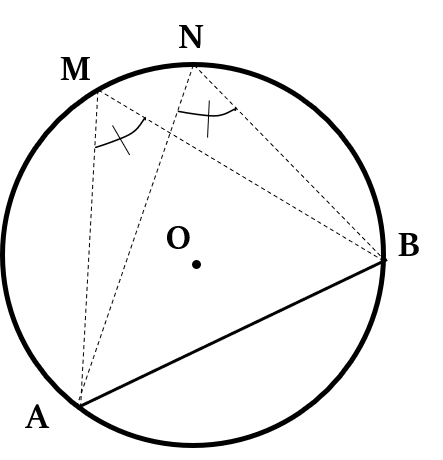
Obviously, angles subtended by a chord/arc in the same segment of a circle will be equal. Geometry

Property 6: Alternate Segment Theorem

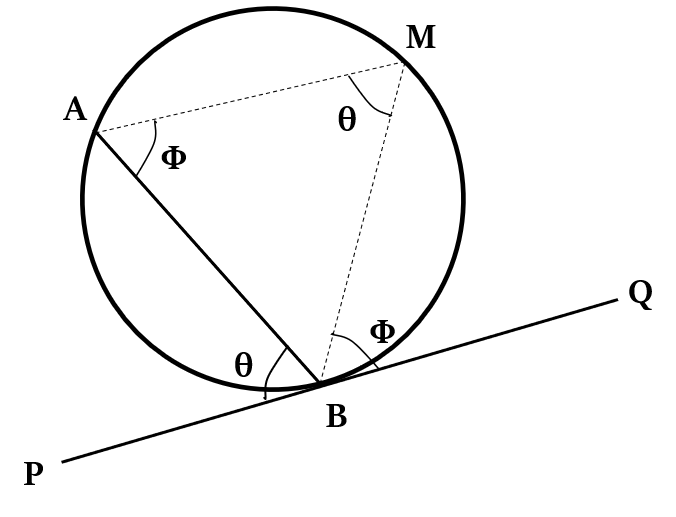
Angle between a chord and a tangent passing through one of the end points of that chord = Angle formed by the chord at the alternate segment Geometry

In the above figure, AB is a chord and the tangent PQ passes through one of the end points of that chord.
So, ∠ABP = ∠AMB

Similarly, in case of the chord BM, ∠MBQ = ∠MAB

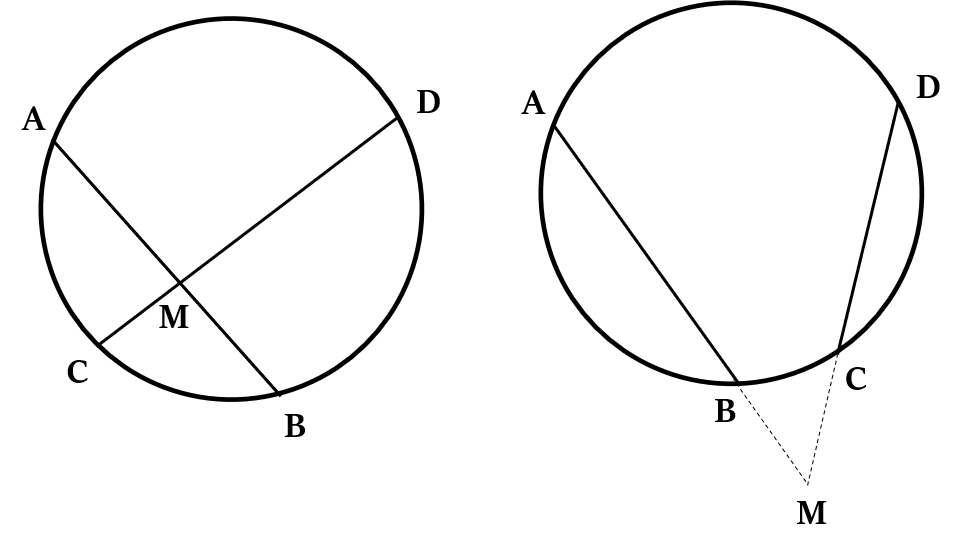
Property 7

If two chords of a circle (say AB and CD), intersect inside a circle or outside a circle (when produced to outside) at a point M, then:
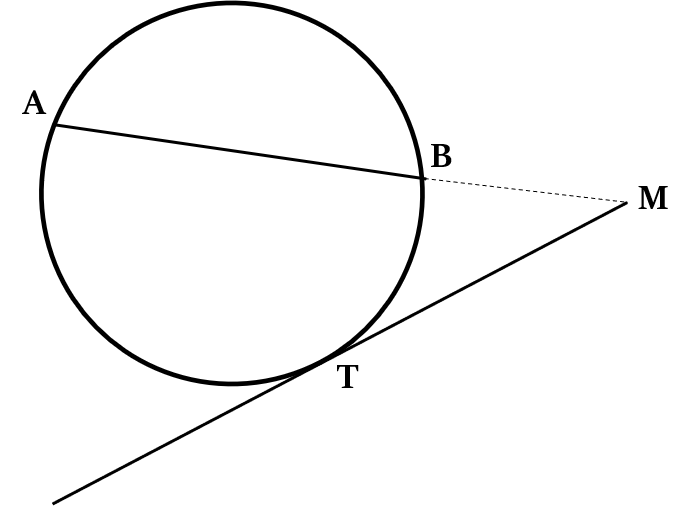
MB × MA = MD × MC. Geometry

One special case of this theorem arises when one of the lines is a tangent, rather than a chord.

When a chord AB is produced to meet a tangent TM at an external point M, then:
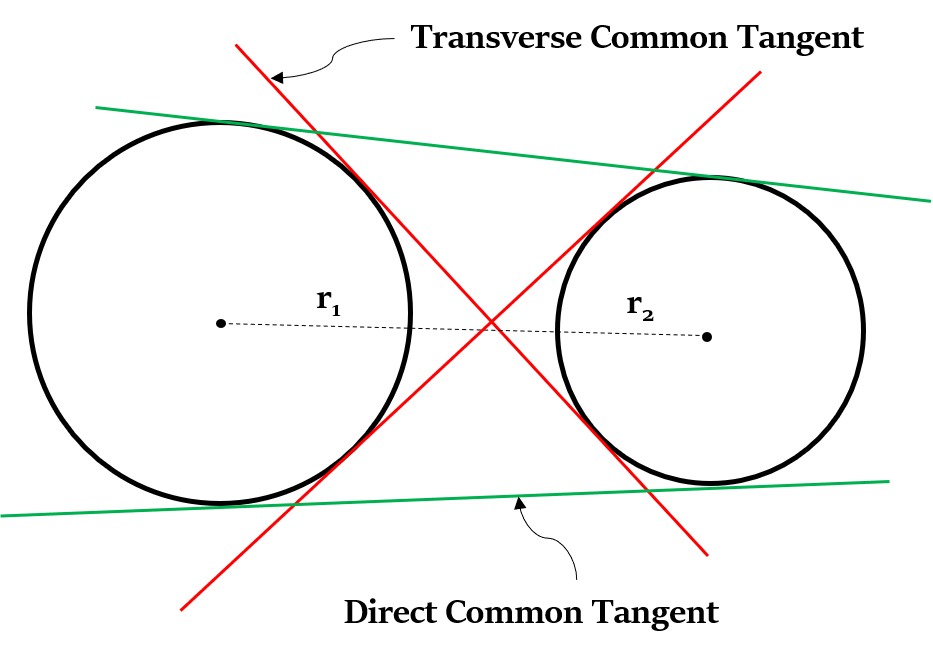
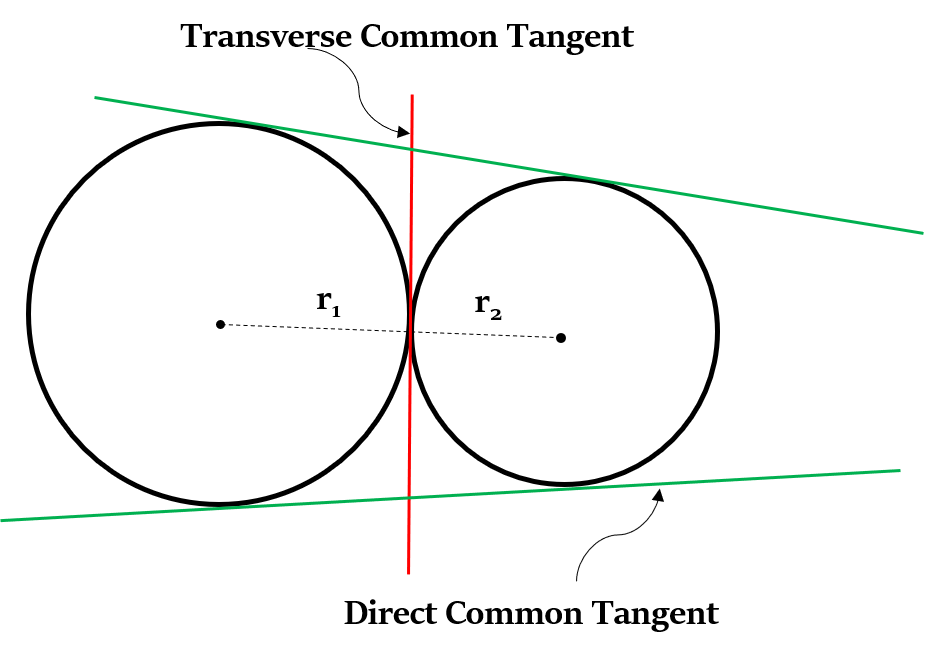
MB × MA = $MT^2$ Geometry

Property 8: Length of Common Tangents

If d - Distance between the centres of two circles; $r_1$ and $r_2$ - radii of two circles

Finding length of Direct Common Tangents

Case 1: Two circles, not touching each other

Length of the direct common tangent = $\sqrt{d^2 - (r_1 - r_2)^2}$ Geometry

Case 2: Two circles touching externally

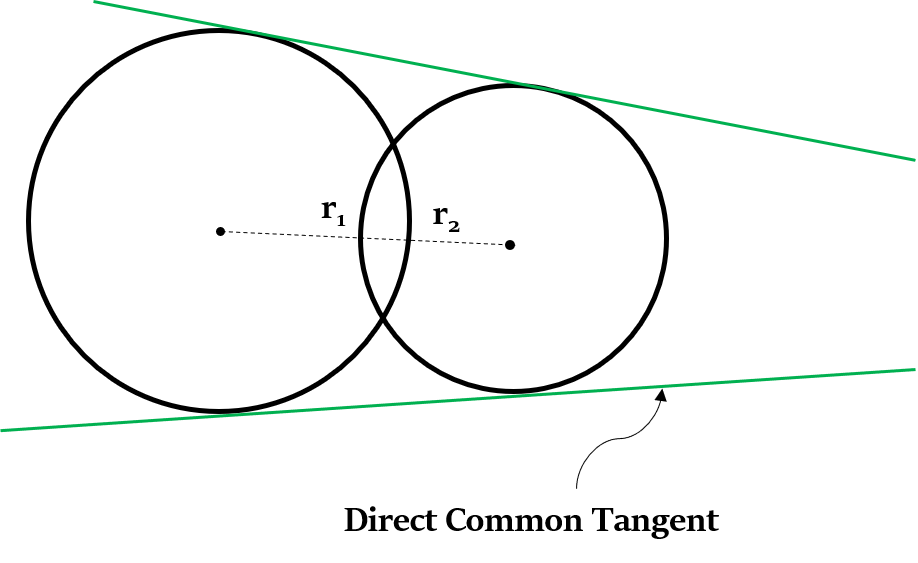
Length of the direct common tangent = 2 $\sqrt{r_1 r_2}$ Geometry

Case 3: Two circles intersecting each other at two points