Similarity Theorems and their applications
Now, as we have already understood the concept of similarity of triangles, let’s see some of the theorems and concepts based on it and their applications.
Theorem 1: Thales theorem
Thales theorem is also known as Basic proportionality theorem.
A line segment, which is parallel to one of the sides of a triangle, cuts the other two sides of that triangle in the same ratio, and it will form a new triangle similar to the original triangle.
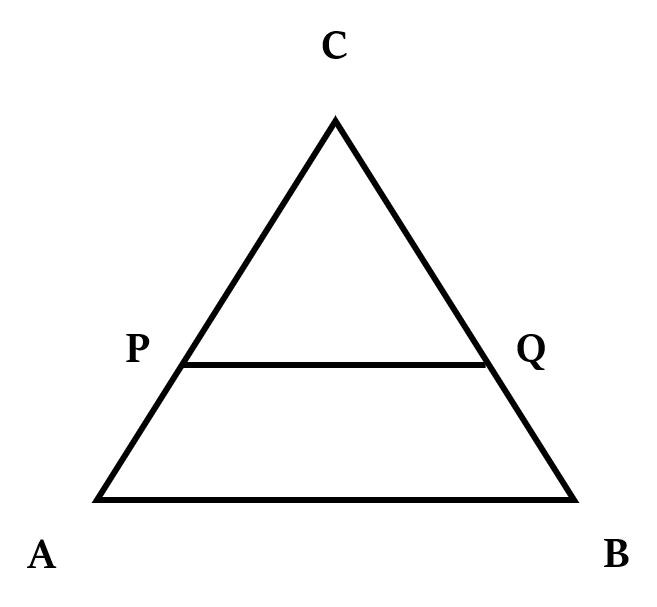
In the above figure, AB ∥ PQ.
As ∠C = ∠C, ∠A = ∠P, ∠B = ∠Q, so ∆ABC ~ ∆PQR
And as ∆ABC ~ ∆PQR, $\frac{AB}{PQ}$ = $\frac{BC}{QC}$ = $\frac{AC}{PC}$
Also, $\frac{AP}{PC}$ = $\frac{BQ}{QC}$
$\frac{AC}{AP}$ = $\frac{BC}{BQ}$
The converse is also true. If a line segment divides two sides of a triangle in the same ratio, then this line segment must be parallel to the third side.
That is, if $\frac{AP}{PC}$ = $\frac{BQ}{QC}$, then it means that PQ ∥ AB.
Now, let us see some special cases of Thales theorem and some related rules.
Special case of Thales theorem
The line segment joining the mid-points of two sides of a triangle is parallel to and half in length of the third side of that triangle.
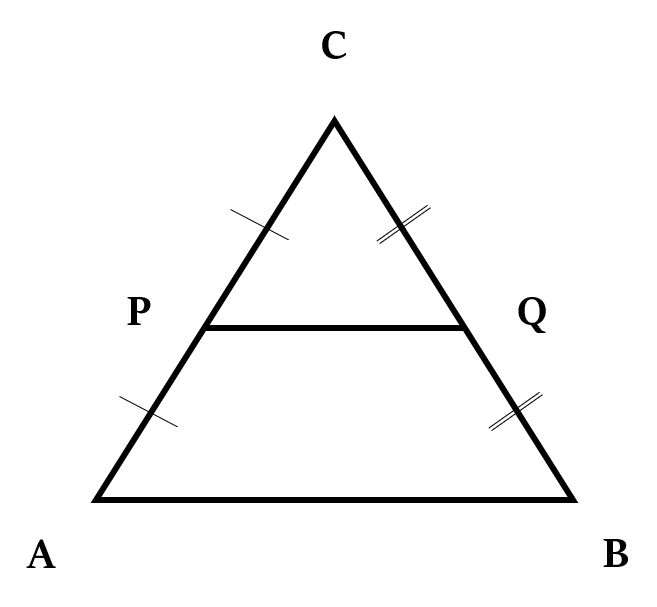
If P and Q are the mid-points of AC and BC, then PQ ∥ AB, and PQ = $\frac{1}{2}$ AB
So, Area of ∆PQC = $\frac{1}{4}$ ∆ABC
And, Area of ∆PQC = $\frac{1}{3}$ □ABQP
In other words, if a line parallel to one of the sides of a triangle bisects the second side, then it will bisect the third side too.
If PQ ∥ AB & P is midpoint of AC, then Q too will be the midpoint of BC.
Related rule
A line segment joining midpoints of two sides of a triangle will bisect the line joining the vertex to the third side too.
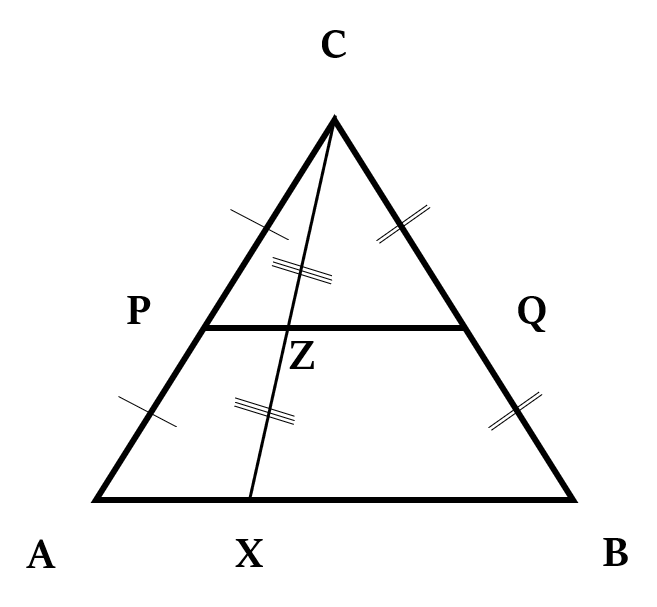
In above figure, as P and Q are the midpoints of sides AC and BC respectively, so CZ = XZ.
Theorem 2
In right-angled triangle, perpendicular drawn from the vertex of right angle to hypotenuse divides the triangle into two parts and forms two small triangles similar to each other and also similar to the original triangle.
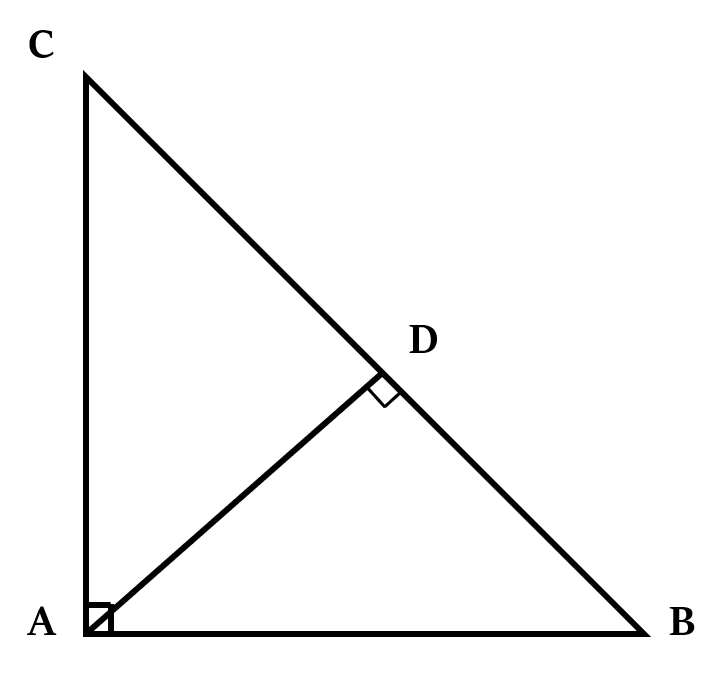
In the above figure, ∆ABC ~ ∆DAB ~ ∆DAC
- $AC^2$ = CB × CD … (1)
- $AB^2$ = BC × BD … (2)
- $AD^2$ = DC × DB … (3)
From these three we can drive three more equations.
Using equations 1 and 2, we get:
$\frac{AC^2}{AB^2}$ = $\frac{CD}{BD}$
Using equations 2 and 3, we get:
$\frac{AB^2}{AD^2}$ = $\frac{BC}{DC}$
Using equations 1 and 3, we get:
$\frac{AC^2}{AD^2}$ = $\frac{CB}{DB}$
- $\frac{1}{AD^2}$ = $\frac{1}{AC^2}$ + $\frac{1}{AB^2}$
or AD = $\frac{AC × AB}{BC}$
Theorem 3: Related to Trapezium
Diagonals of trapezium (AB ∥ CD) divide it into four triangles.
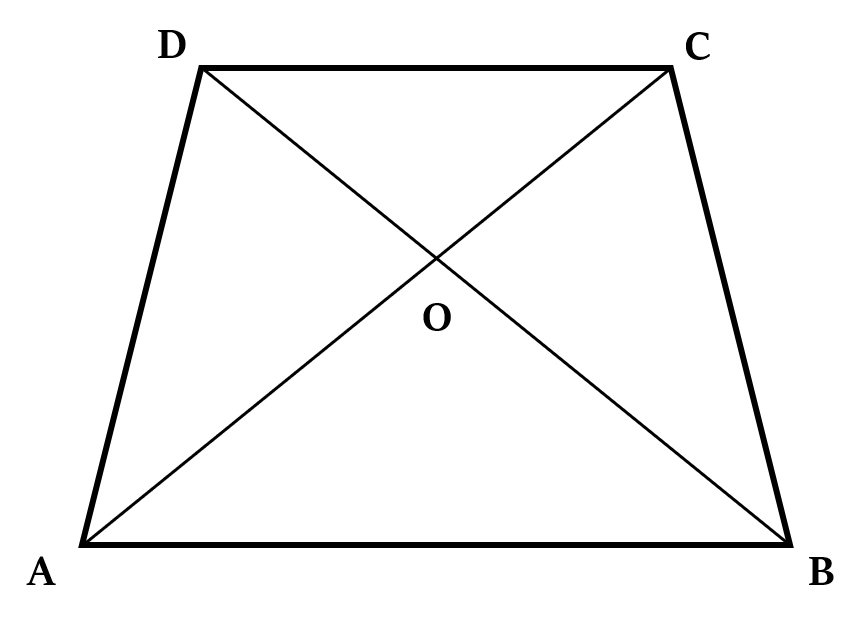
- Two triangles along the parallel side are similar, i.e. ∆DOC ~ ∆AOB
- Two triangles along the non-parallel sides are equal in area, i.e. Area of ∆AOD = Area of ∆BOC