Introduction to Coordinate Geometry
What is Coordinate Geometry?
Coordinate Geometry is a system of geometry where we use ordered pair of numbers to describe the position of points on a plane. The ordered pair of numbers are called coordinates of that point.
This system was developed by a French mathematician, René Descartes (1596 – 1650). That’s why we also call coordinates as Cartesian coordinates.
Moreover, René Descartes proposed that even lines and curves could be described by equations using this technique.
Now, let’s study this system of geometry in detail.
Cartesian Co-ordinate System
Cartesian Co-ordinate System is used to denote the exact position of a point on a plane. For this we use concepts of axes, and quadrants.
Co-ordinates Axes
Two mutually perpendicular lines on a plane, passing through a point are called Co-ordinates Axes.
- The point of intersection of the two axes is called the Origin.
- The horizontal line is called the X-axis or the abscissa.
- The vertical line is called the Y-axis or the ordinate.
Quadrants
The two perpendicular axes divides the 2-D plane in four sectors. These sectors are called Quadrants, and are named as per the sign of x and y.


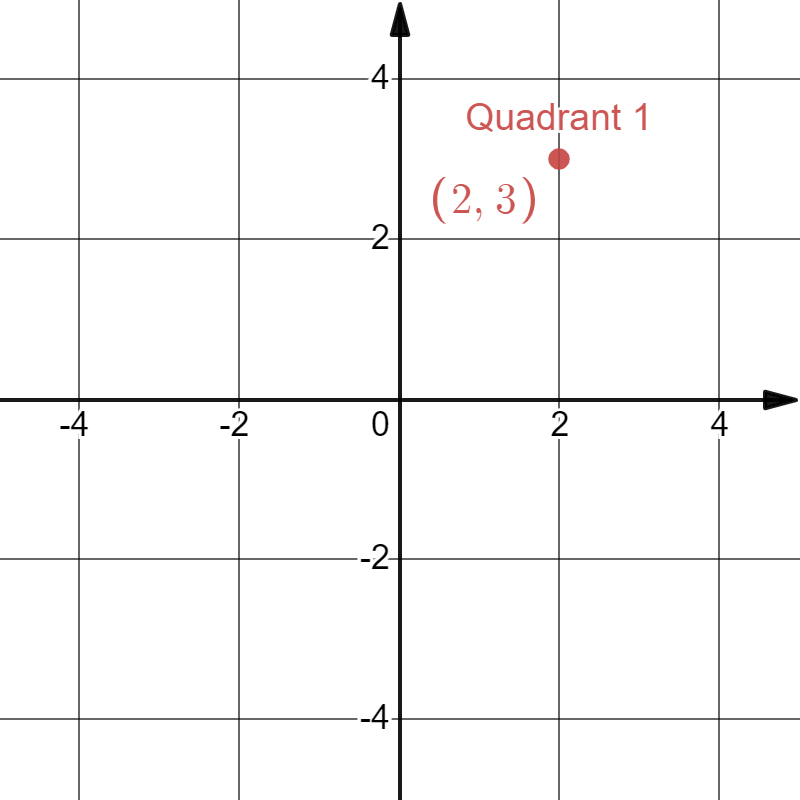
Point of the type (+, +) lies in the 1st quadrant. E.g. (2, 3)
Point of the type (-, +) lies in the 2nd quadrant. E.g. (-2, 3)
Point of the type (-, -) lies in the 3rd quadrant. E.g. (-2, -3)
Point of the type (+, -) lies in the 4th quadrant. E.g. (2, -3)
Coordinates of a Point
As already mentioned, coordinates of a point are a pair of numbers that define its exact location on a two-dimensional plane.
- To state the position of a point with reference to the two axes, we just use normal coordinates.
- To state the position of a point with reference to the origin, we use polar coordinates.
Let’s study them in more detail.
Ordered Pair
We write the coordinates of a point in the form of an ordered pair. For example, (3, 7), (-4, 2), (2.5, -1), etc.
The first number in the ordered pair indicates the position of the point with respect to the X-axis.
The second number in the ordered pair indicates the position of the point with respect to the Y-axis.
For example, point P (3, 5) is:

- at a distance of 3 units from the Y-axis, in the direction of positive side of X-axis.
- at a distance of 5 units from the X-axis, in the direction of positive side of Y-axis.
Polar Coordinates
To denote the position of a point with respect to the origin (rather than the axes), we use Polar Coordinates.
To indicate the position of a point, polar coordinates use:
- the distance of a point from the origin (denoted by r), and
- the angle that the line joining the origin and the point makes with the X-axis (denoted by θ or Φ)

Polar coordinates of point P are: (r cos Φ, r sin Φ)
Converting normal coordinates into polar coordinates
If we have a point P (x, y), we can easily find its polar coordinates. Let’s take the example of the point P (
The distance of a point P (x, y) from the origin, r =
tan Φ =
It means, Φ = 30°
So, x = r cos Φ = 2 cos 30°
y = r sin Φ = 2 sin 30°
Polar coordinates of point P (
