Introduction to Trigonometry

What is Trigonometry?

Trigonometry is a branch of mathematics, that studies relationships involving sides and angles of triangles.

So, in layman’s terms, we can say that Trigonometry is the study of triangles.

The word ‘Trigonometry’ has been made by combining three Greek words:

‘tri’ - it means three,
‘gon’ - it means sides and
‘metron’ - it means measure

Functions in trigonometry

Functions in trigonometry are basically the ratios of the sides of a right-angled triangle. They express the relationship between the acute angle of a right-angled triangle and the length of its sides.

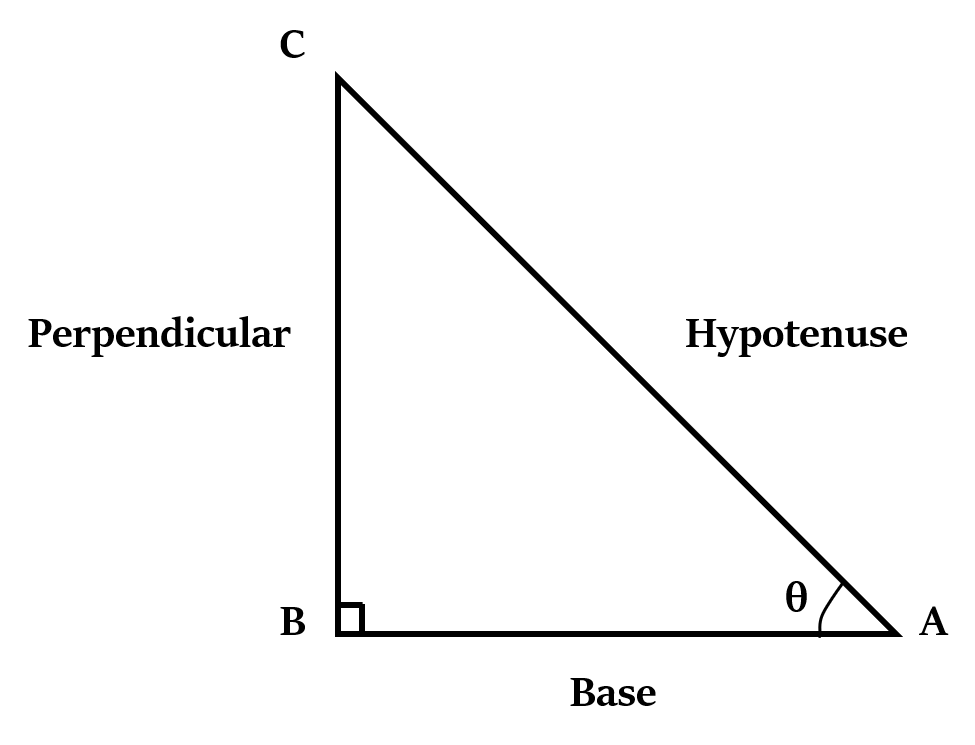
Have a look at the following figure of a right-angled triangle. Trigonometry

The main functions in trigonometry are:

Name	Trigonometry function
Sine	sin θ = $\frac{Perpendicular}{Hypotenuse}$ = $\frac{BC}{AC}$
Cosine	cos θ = $\frac{Base}{Hypotenuse}$ = $\frac{AB}{AC}$
Tangent	tan θ = $\frac{sin \hspace{1ex} θ}{cos \hspace{1ex} θ}$ = $\frac{Perpendicular}{Base}$ = $\frac{BC}{AB}$
Cosecant	cosec θ = $\frac{1}{sin \hspace{1ex} θ}$ = $\frac{Hypotenuse}{Perpendicular}$ = $\frac{AC}{BC}$
Secant	sec θ = $\frac{1}{cos \hspace{1ex} θ}$ = $\frac{Hypotenuse}{Base}$ = $\frac{AC}{AB}$
Cotangent	cot θ = $\frac{1}{tan \hspace{1ex} θ}$ = $\frac{cos \hspace{1ex} θ}{sin \hspace{1ex} θ}$ = $\frac{Base}{Perpendicular}$ = $\frac{AB}{BC}$

Sine, Cosine, Tangent, Cosecant, Secant and Cotangent are often abbreviated as sin, cos, tan, cosec, sec, and cot respectively.

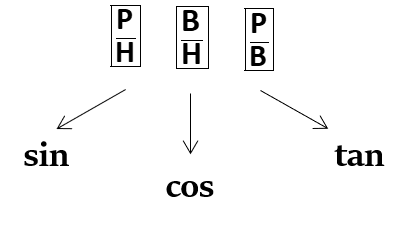To remember these ratio, we can memorize them using a mnemonic: Trigonometry

P → Perpendicular; B → Base; H → Hypotenuse

Values of Trigonometric Functions

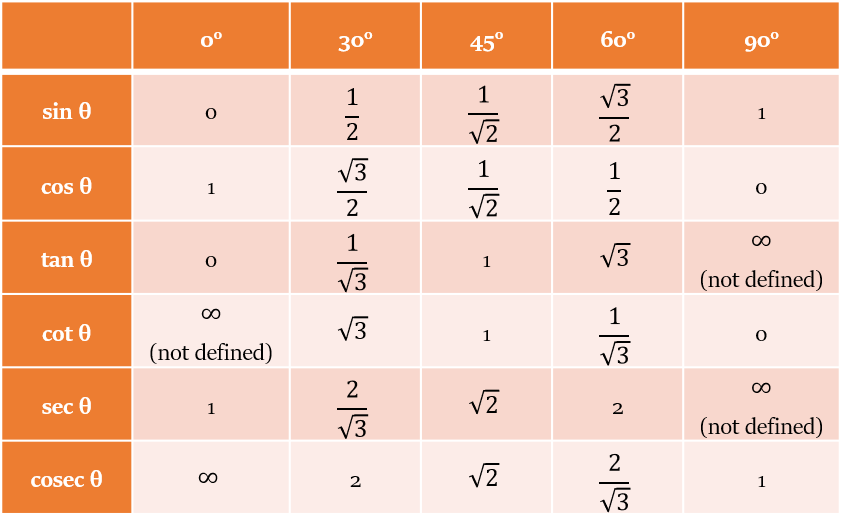
Have a look at the values of Trigonometric Functions for some important angles from 0° to 90°. Trigonometry

You should remember these values.

Just remember sin and cos values, and maybe tan values too. Though you may find out the tan values by dividing sin values by corresponding cos values.

Values of cosec, sec and cot are reciprocal of the values of sin, cos and tan respectively.

$\frac{1}{0}$ = ∞; $\frac{-1}{0}$ = -∞

Both of these are not defined.

Signs of Trigonometric Functions

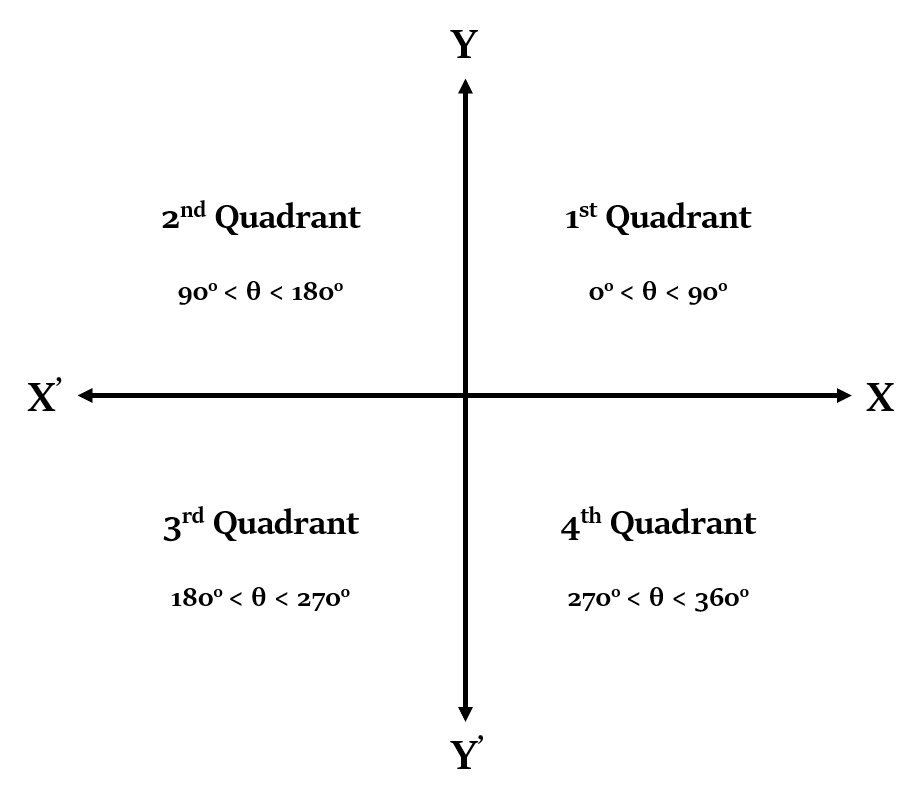
So, now we know the values of Trigonometric Functions for angles such as 30°, 45°, 90° etc. All of these angles fall in the first quadrant. Trigonometry

But what about such angles in other quadrants, e.g. 120°, 225°, 180° etc. ?

Here are the three steps that you need to follow:

Step 1: Find out the quadrant to which the angle belongs.
Step 2: Use the appropriate formula, to find the value of the concerned Trigonometric Function.
Step 3: Don’t forget to use the appropriate sign.

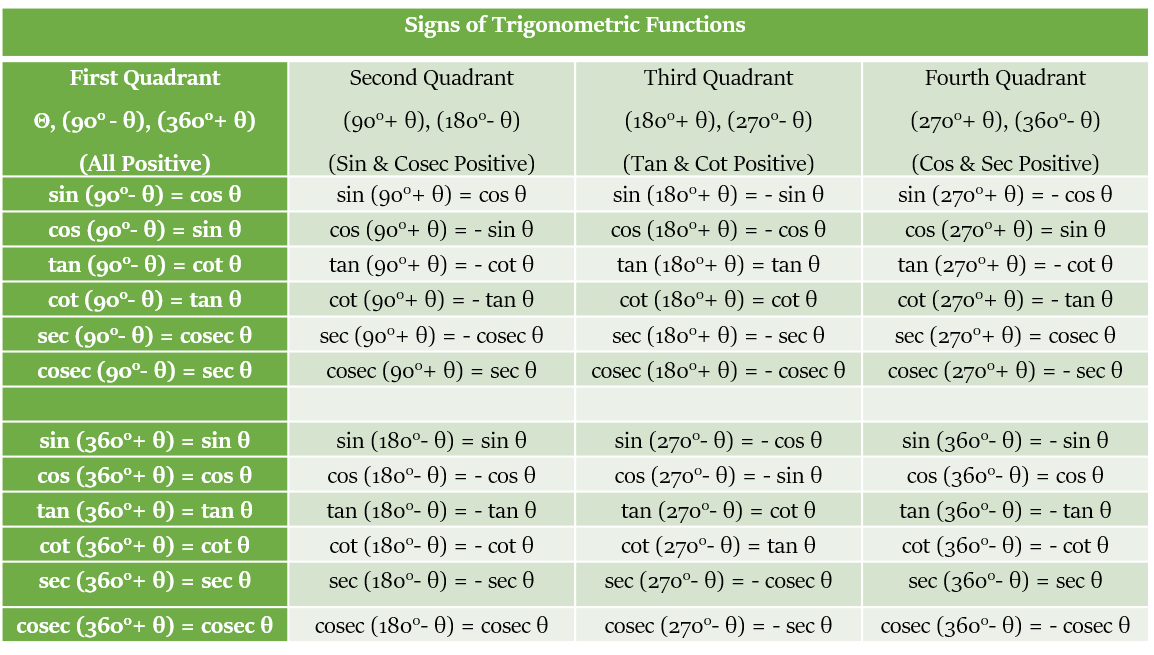
We can draw following conclusions from the above table:

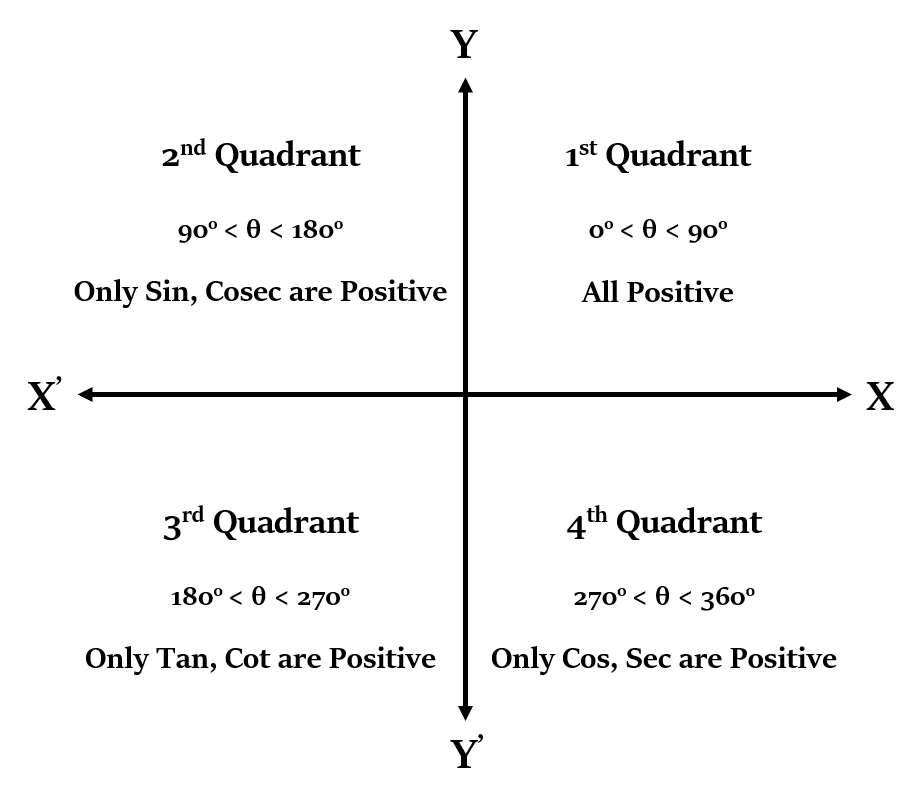
The sign of the Trigonometric Function will depend on which quadrant the angle falls in. It can be represented using the following figure:
When the angle is a multiple of 180°, e.g. 0°, 180°, 360°, … etc., then trigonometric function will not get changed. For example, sin (180° - θ) = sin θ, tan (180° + θ) = tan θ etc.
When the angle is an odd multiple of 90°, e.g. 90°, 270°, … etc., then trigonometric function will get changed. For example, cos (90° - θ) = sin θ, sin (270° - θ) = - cos θ