Introduction to Vectors

What are Vectors in Maths?

Vectors are the objects that are denoted by an arrow. They have both:

• Magnitude – denoted by the length of the line of the arrow.
• Direction – denoted by the head of the arrow.

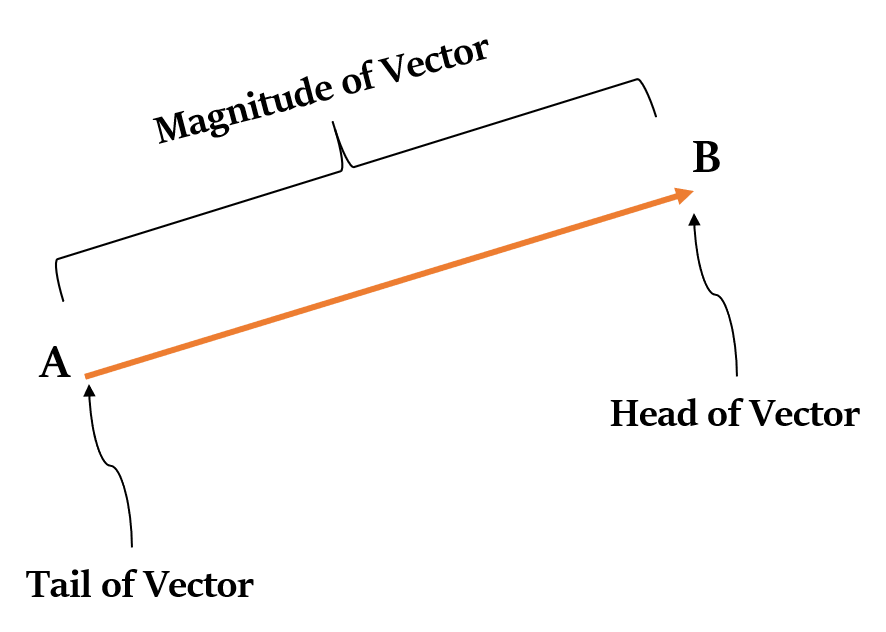
Vectors in Maths are also known as Euclidean vectors, Geometric vectors, or Spatial vectors.

Vector is represented by an arrow over the name of the vector, e.g. $\overrightarrow{a}$

Reverse Vector

Reverse vector of a given vector $\overrightarrow{a}$ will be -$\overrightarrow{a}$. It will have the same magnitude as the original vector, but opposite direction.

Components of Vectors

A vector in the x-y plane has two components:

• Horizontal Component
• Vertical Component

While solving questions involving vectors, we will often break vectors into their x and y components. This makes our task much easier.

If we have a vector $\overrightarrow{a}$, that makes an angle of θ with the horizontal X-axis, then:

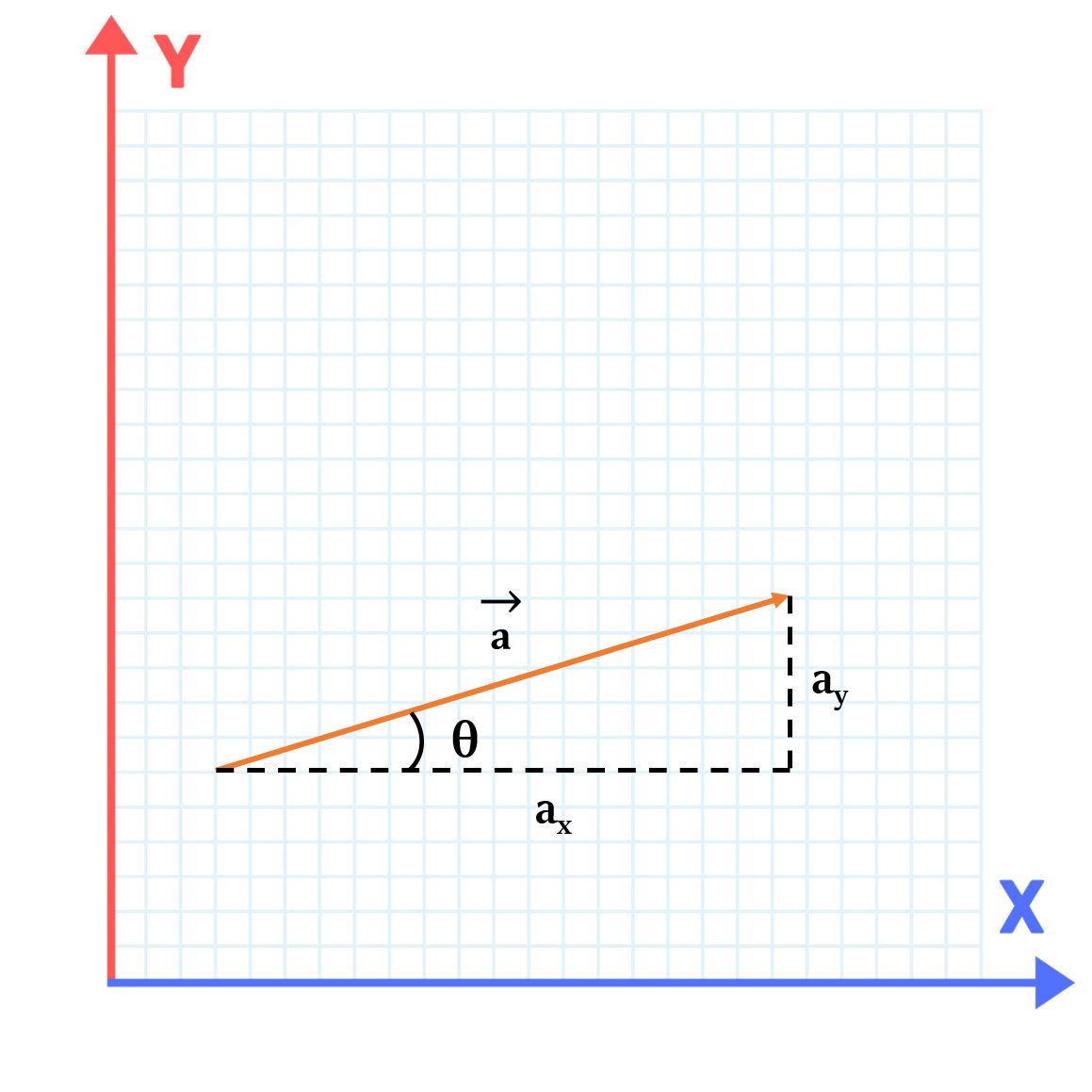
• Horizontal Component of the vector, $a_x$ = a cos θ
• Vertical Component of the vector, $a_y$ = a sin θ

Magnitude of Vector

Magnitude of Vector is the length of the vector. It is represented by two vertical lines on both the sides of the given vector, e.g. $\left\lVert a \right\rVert$

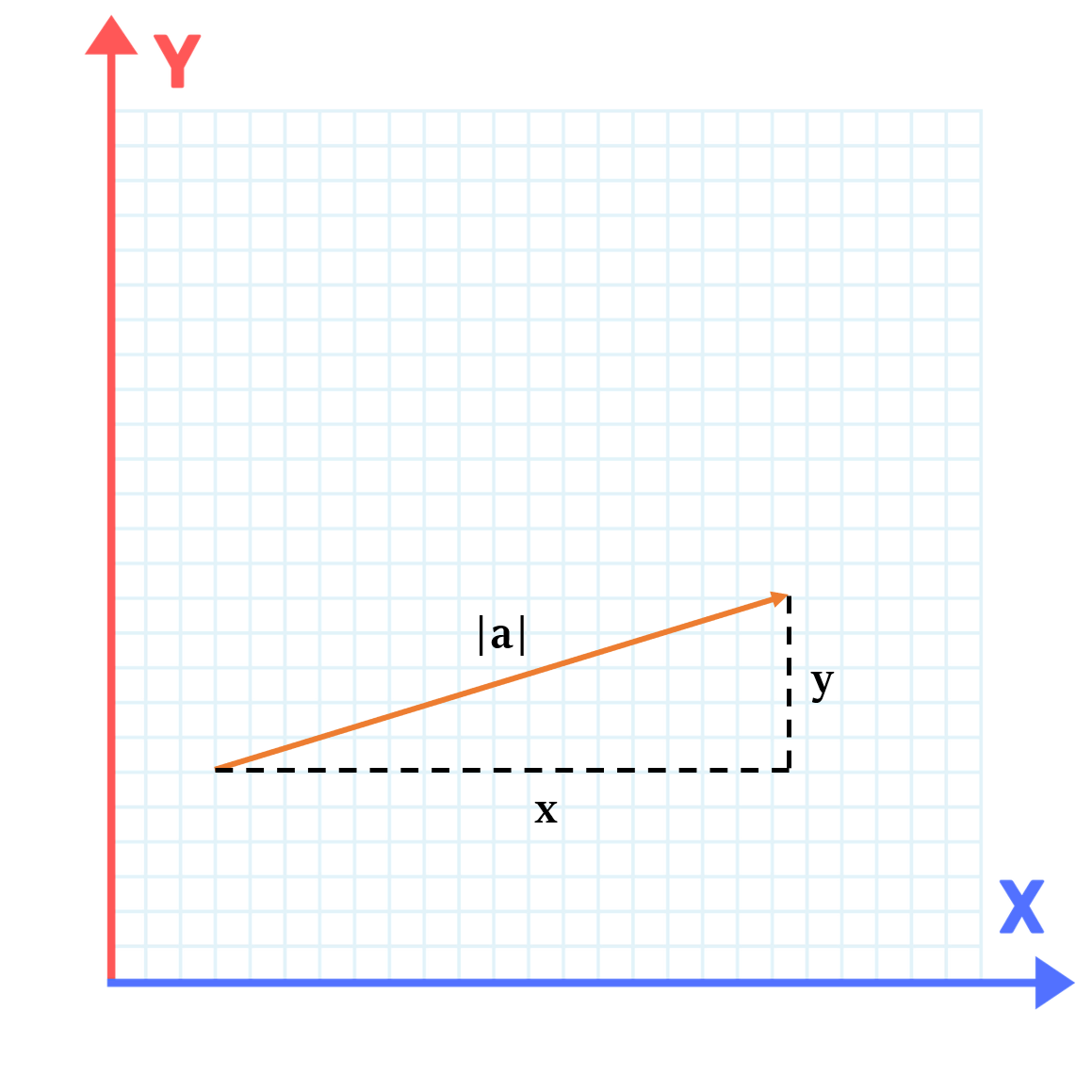
$\left\lVert a \right\rVert = √(x^2 + y^2)$

Unit Vector

If a vector has unit length, i.e. its magnitude is equal to one, then it’s called a unit vector. It’s represented by a cap or hat above the name of the vector, e.g. $\hat{a}$

Normalising a vector is the process of finding the unit vector of any given vector. To find the unit vector, we just need to divide the given vector by its magnitude.
So, $\hat{a} = \frac{a}{\left\lVert a \right\rVert}$

We use unit vector, when we are just interested in the direction of a vector.

Zero Vector

If a vector has no length, i.e. its magnitude is equal to zero, then it’s called a zero vector. It’s represented by $\overrightarrow{0}$, or 0.

Sum of any vector with zero vector will result in that vector itself. That is, $\overrightarrow{a} + \overrightarrow{0} = \overrightarrow{a}$

Operations on Vectors

We can perform operations like Addition, Subtraction, Multiplication on vectors.

Addition of Vectors

To add two vectors $\overrightarrow{a}$ and $\overrightarrow{b}$, we can use the graphical method.

To do so, we place the two vectors in such a manner that the tail of one vector is touching the head of the other vector.

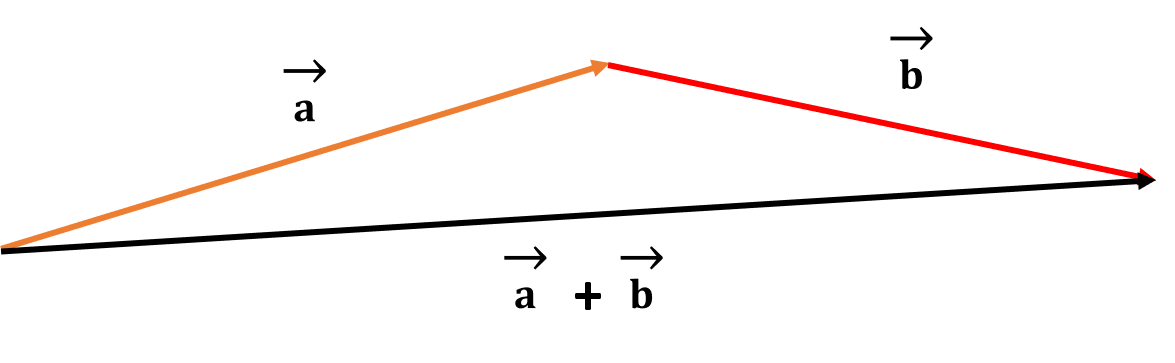
As shown above, their sum $\overrightarrow{a} + \overrightarrow{b}$ will be the vector joining the tail of the first vector with the head of the second vector.

Subtraction of Vectors

Subtraction of vectors is similar to addition of vectors. Here, we just add the reverse vector of the vector being subtracted.

That is, $\overrightarrow{a} - \overrightarrow{b} = \overrightarrow{a} + \overrightarrow{(-b)}$

Multiplication of Vectors

There are various types of multiplications possible when vectors are involved. Let’s see them.

Scalar Multiplication

When a vector is multiplied by a scalar quantity, then it’s called a Scalar Multiplication.

Scalar Multiplication may change the magnitude of the vector, i.e. it may scale down (make it smaller) or scale up (make it larger) the vector.

Scalar Multiplication with positive numbers will not change the direction of the vector. However, Scalar Multiplication with a negative scalar will reverse the direction of the vector.

For example, 3 . $\overrightarrow{a} = \overrightarrow{3a}$
0 . $\overrightarrow{a} = \overrightarrow{0}$ (The zero on the left is the number 0, while the zero on the right is the vector 0.)
1 . $\overrightarrow{a} = \overrightarrow{a}$
(-1) . $\overrightarrow{a} = \overrightarrow{(-a)}$

Vector Multiplication

When we multiply two or more vectors, then it is called Vector Multiplication.

There are two types of vector multiplications:

• Cross Product – it results in a vector quantity
• Dot Product – it results in a scalar quantity

Let’s study them in detail.

Cross Product of Vectors

As already mentioned, the cross product of two vectors results in a vector quantity (i.e. a quantity that has both magnitude and direction). We use cross sign (×) to represent it.

For example, cross product of two vectors will be represented as $\overrightarrow{a} × \overrightarrow{b}$

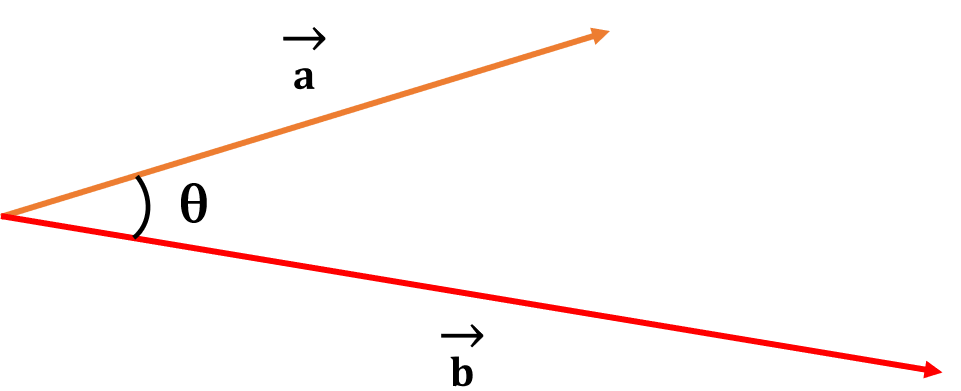
$\overrightarrow{a} × \overrightarrow{b}$ = $\left\lVert a \right\rVert$ $\left\lVert b \right\rVert$ sin θ $\hat{n}$

Where $\left\lVert a \right\rVert$ and $\left\lVert b \right\rVert$ are the magnitudes of the vectors $\overrightarrow{a}$ and $\overrightarrow{b}$ respectively, and θ is the angle between those two vectors.

$\hat{n}$ is a unit vector. It shows the direction of the multiplication of these two vectors.

Dot Product of Vectors

As already mentioned, the dot product of two vectors always results in a scalar quantity (i.e. a quantity that only has magnitude and no direction). We use dot sign (.) to represent it.

For example, dot product of two vectors will be represented as $\overrightarrow{a} . \overrightarrow{b}$

$\overrightarrow{a} . \overrightarrow{b}$ = $\left\lVert a \right\rVert$ $\left\lVert b \right\rVert$ cos θ