Coordinate Geometry - Triangle
Area of a Triangle
We can find the area of a triangle if we know the coordinates of its vertices. Let’s see how.
If the vertices of a ∆ABC are A ($x_1$, $y_1$), B ($x_2$, $y_2$) and C ($x_3$, $y_3$), then:
Area of the triangle, ∆ = $ \frac{1}{2} \begin{vmatrix} x_1 & y_1 & 1 \newline x_2 & y_2 & 1 \newline x_3 & y_3 & 1 \end{vmatrix}$ = $ \frac{1}{2} |x_1 (y_2 – y_3) + x_2 (y_3 – y_1) + x_3 (y_1 – y_2)|$ = $ \frac{1}{2} |(x_1 y_2 – x_2 y_1) + (x_2 y_3 – x_3 y_2) + (x_3 y_1 – x_1 y_3)|$
We have placed modulus signs in the above formula, because area of a triangle (or any other figure) can never be negative.
In fact, we can generalize the above formula for any polygon.
If we have a polygon, whose vertices are ($x_1$, $y_1$), ($x_2$, $y_2$), ($x_3$, $y_3$) …. ($x_n$, $y_n$), then:
Area of the polygon = $ \frac{1}{2} |(x_1 y_2 – x_2 y_1) + (x_2 y_3 – x_3 y_2) + (x_3 y_4 – x_4 y_3) + …. +$ $(x_{n - 1} y_n – x_n y_{n - 1}) + (x_n y_1 – x_1 y_n)|$
Coordinates of Important Points in a Triangle
Coordinates of Centroid
If the vertices of a ∆ABC are A ($x_1$, $y_1$), B ($x_2$, $y_2$) and C ($x_3$, $y_3$), then:
Coordinates of its Centroid = $(\frac{x_1 + x_2 + x_3}{3}, \frac{y_1 + y_2 + y_3}{3})$
Centroid (G) is the point of intersection of the medians of a triangle.
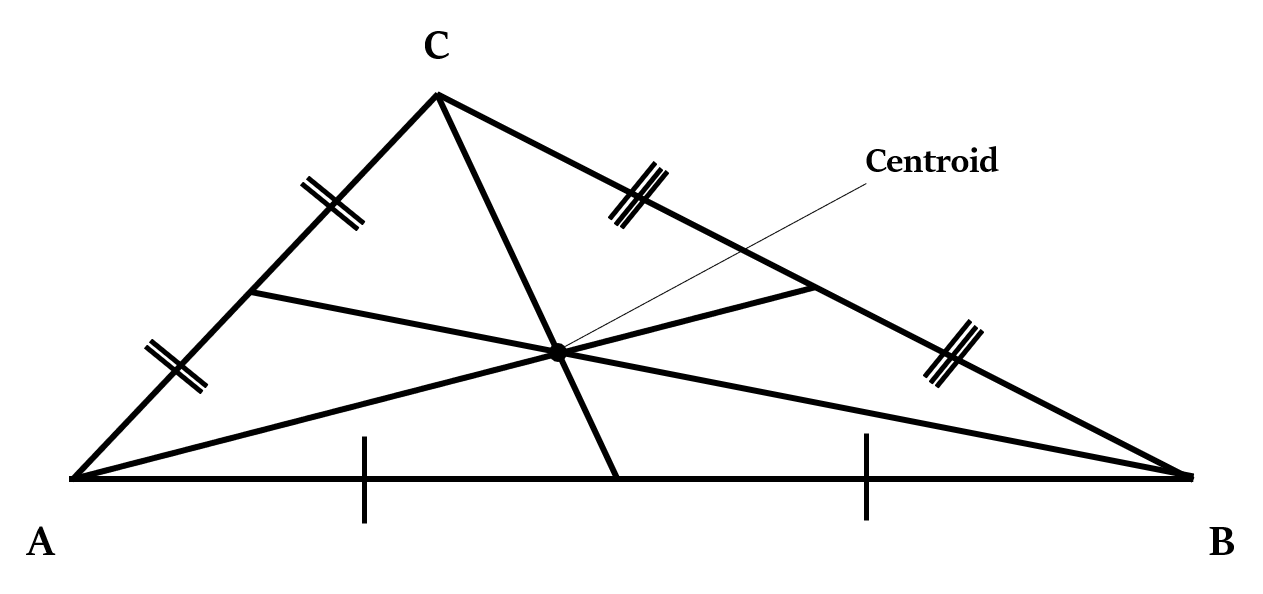
Median is a line segment that joins any vertex of the triangle with the mid-point of its opposite side.
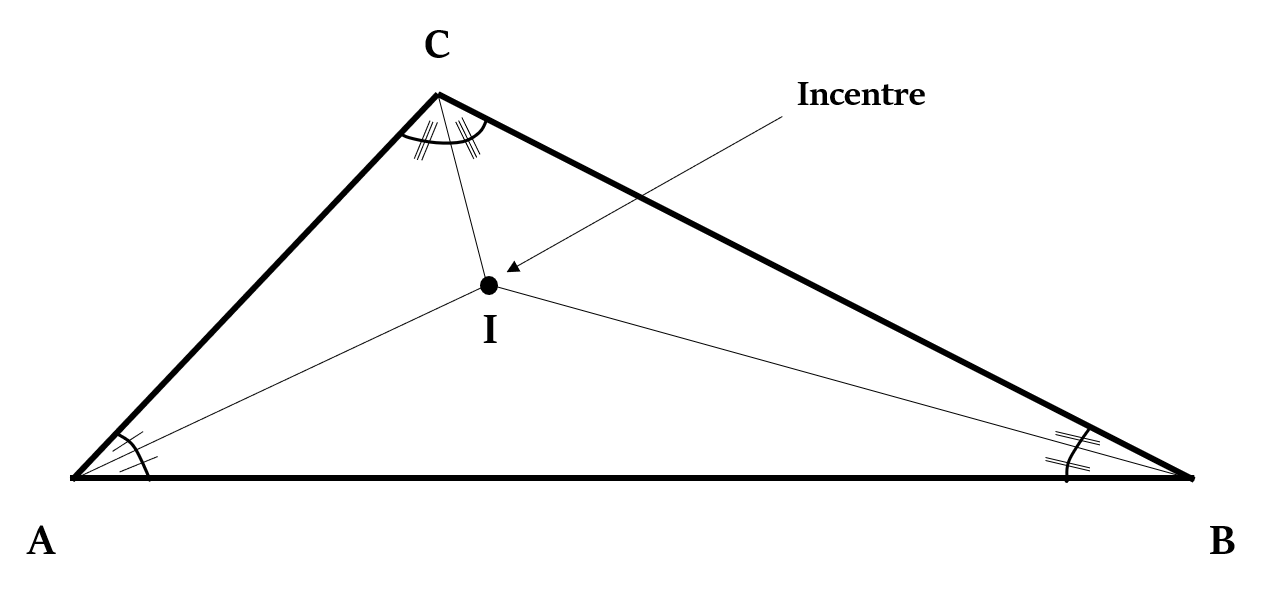
Coordinates of In-Centre
If the vertices of a ∆ABC are A ($x_1$, $y_1$), B ($x_2$, $y_2$) and C ($x_3$, $y_3$), and the length of their opposite sides are a, b and c, then:
Coordinates of its In-Centre = $(\frac{ax_1 + bx_2 + cx_3}{a + b + c}, \frac{ay_1 + by_2 + cy_3}{a + b + c})$
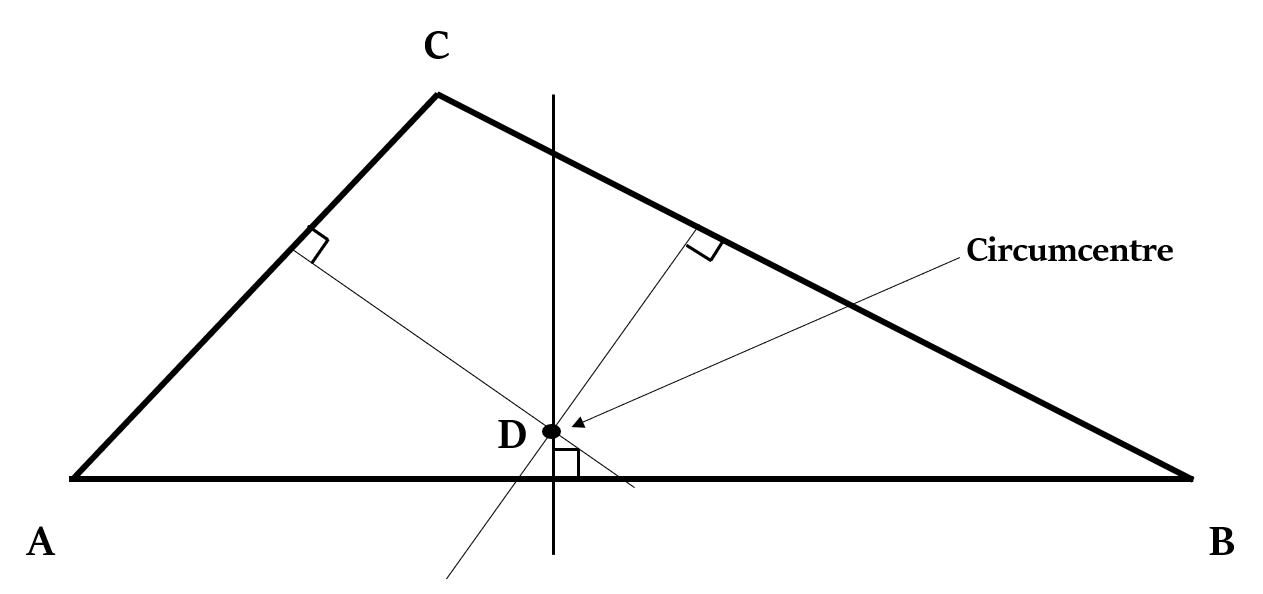
Coordinates of Circumcenter
If the vertices of a ∆ABC are A ($x_1$, $y_1$), B ($x_2$, $y_2$) and C ($x_3$, $y_3$), then:
Coordinates of its Circumcenter = $(\frac{x_1 \hspace{1ex} sin 2A \hspace{1ex} + \hspace{1ex} x_2 \hspace{1ex} sin 2B \hspace{1ex} + \hspace{1ex} x_3 \hspace{1ex} sin 2C}{sin 2A + sin 2B + sin 2C}, \frac{y_1 \hspace{1ex} sin 2A \hspace{1ex} + \hspace{1ex} y_2 \hspace{1ex} sin 2B \hspace{1ex} + \hspace{1ex} y_3 \hspace{1ex} sin 2C}{sin 2A + sin 2B + sin 2C})$
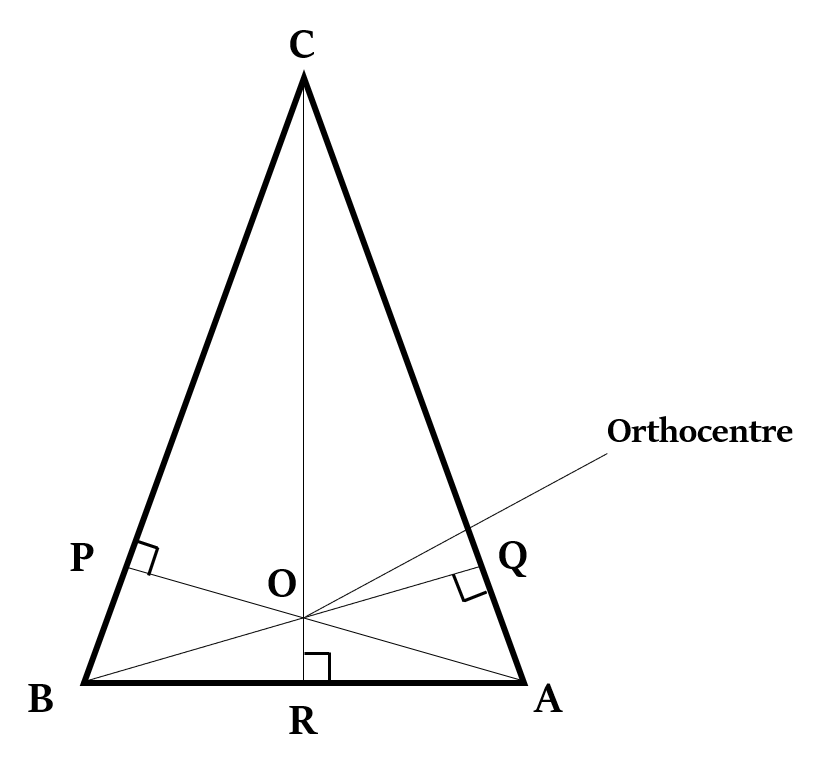
Coordinates of Orthocenter
If the vertices of a ∆ABC are A ($x_1$, $y_1$), B ($x_2$, $y_2$) and C ($x_3$, $y_3$), then:
Coordinates of its Orthocenter = $(\frac{x_1 \hspace{1ex} tan A \hspace{1ex} + \hspace{1ex} x_2 \hspace{1ex} tan B \hspace{1ex} + \hspace{1ex} x_3 \hspace{1ex} tan C}{tan A + tan B + tan C}, \frac{y_1 \hspace{1ex} tan A \hspace{1ex} + \hspace{1ex} y_2 \hspace{1ex} tan B \hspace{1ex} + \hspace{1ex} y_3 \hspace{1ex} tan C}{tan A + tan B + tan C})$
