Coordinate Geometry - Equation of Lines with respect to other lines
We have already seen the different ways in which we can write the equation of a single line. In this article, we will learn how to write equations of multiple lines.
Equation of a line with respect to another line
Equations of a straight line that passes through a point A ($x_1$, $y_1$) and makes an angle of θ with the line y = mx + c are:
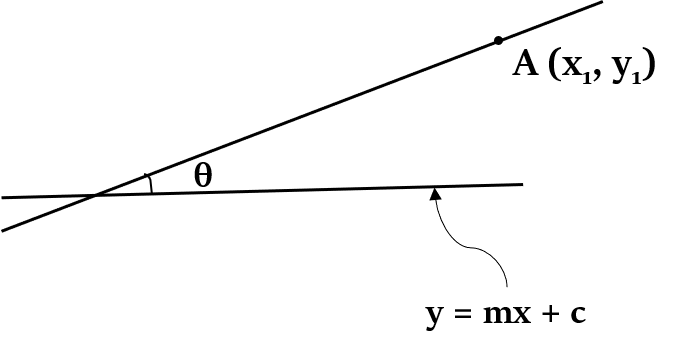
$y - y_1 = \frac{m \hspace{1ex} ± \hspace{1ex} tan θ}{1 \hspace{1ex} ∓ \hspace{1ex} m \hspace{1ex} tan θ} (x - x_1)$
Equation of a line with respect to two other lines
Equation of a line pssing through intersection point
A line that passes through the point of intersection of the lines $a_1x + b_1y + c_1$ = 0 and $a_2x + b_2y + c_2$ = 0, can be represented by the following equation:
$(a_1x + b_1y + c_1) + λ (a_2x + b_2y + c_2$) = 0, where λ is a constant.
Point of intersection of two lines
If we have two lines $a_1x + b_1y + c_1$ = 0 and $a_2x + b_2y + c_2$ = 0, then:
$\frac{x}{b_1 c_2 – b_2 c_1} = \frac{y}{c_1 a_2 – c_2 a_1} = \frac{1}{a_1 b_2 – a_2 b_1}$
Thus, point of intersection of these two lines = $\frac{b_1 c_2 – b_2 c_1}{a_1 b_2 – a_2 b_1}, \frac{c_1 a_2 – c_2 a_1}{a_1 b_2 – a_2 b_1}$
Where $a_1 b_2 – a_2 b_1$ ≠ 0
Equations of Angle Bisectors
The equations of the angle bisectors of two line $a_1x + b_1y + c_1$ = 0 and $a_2x + b_2y + c_2$ = 0, can be represented as follows:
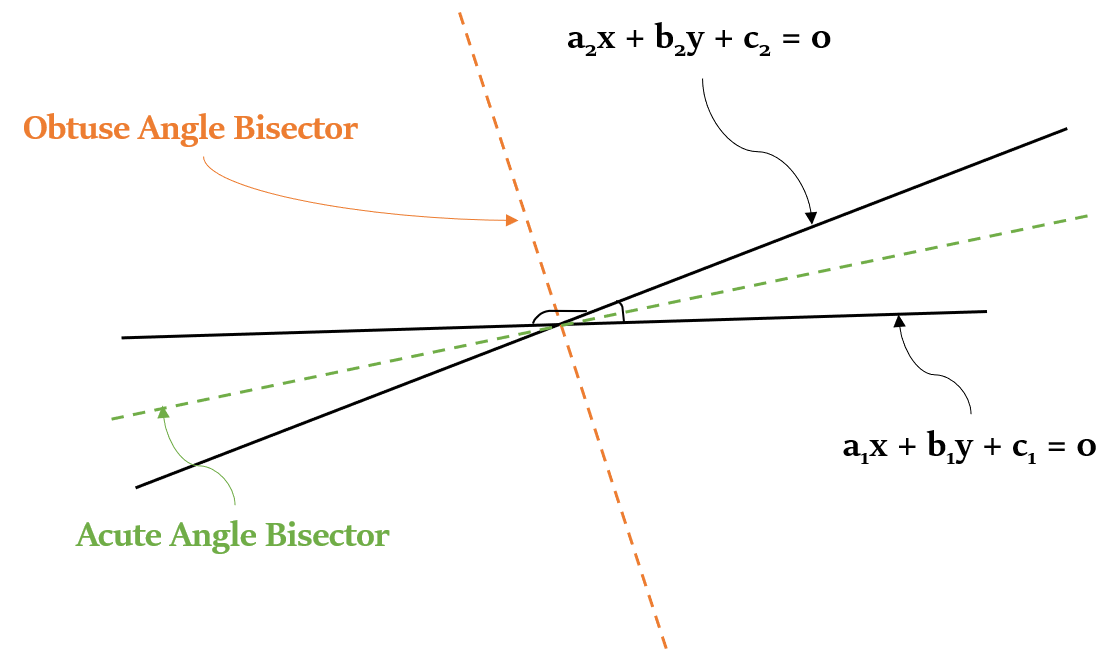
$\frac{a_1x + b_1y + c_1}{\sqrt{a_1^2 + b_1^2}} = ± \frac{a_2x + b_2y + c_2}{\sqrt{a_2^2 + b_2^2}}$
How to determine which bisector equation is of Acute and Obtuse angle?
Now, let us see how to find:
- whether the origin lies in the acute angle or obtuse angle between the lines.
- which bisector equation corresponds to acute angle bisector and obtuse angle bisector.
Step I: Ensure that both $c_1$ and $c_2$ are positive. If one of them, or both are negative, then make them positive by multiplying both the sides of the concerned equation by -1.
Step II: Find out the sign of $a_1 a_2 + b_1 b_2$.
If $a_1 a_2 + b_1 b_2$ > 0, then:
- the origin lies in the obtuse angle, and
- the “+” symbol gives the bisector of the obtuse angle. That is, Equation of the bisector of the obtuse angle will be: $\frac{a_1x + b_1y + c_1}{\sqrt{a_1^2 + b_1^2}} = \frac{a_2x + b_2y + c_2}{\sqrt{a_2^2 + b_2^2}}$
If $a_1 a_2 + b_1 b_2$ < 0, then:
- the origin lies in the acute angle, and
- the “+” symbol gives the bisector of the acute angle. That is, Equation of the bisector of the acute angle will be: $\frac{a_1x + b_1y + c_1}{\sqrt{a_1^2 + b_1^2}} = \frac{a_2x + b_2y + c_2}{\sqrt{a_2^2 + b_2^2}}$
Angle between two lines
If θ is the angle between two lines y = $m_1x + c_1$ and y = $m_2x + c_2$, then:
tan θ = $|\frac{m_2 - m_1}{1 + m_2 m_1}|$ or $|\frac{m_1 - m_2}{1 + m_1 m_2}|$
If θ is the angle between two lines $a_1x + b_1y + c_1$ = 0 and $a_2x + b_2y + c_2$ = 0, then:
tan θ = $\frac{a_2 b_1 – a_1 b_2}{a_1 a_2 + b_1 b_2}$