Coordinate Geometry - Reflection of a Point
What is Reflection?
Reflection is a phenomenon in which a figure (a point, line, etc.) is turned into its mirror image by flipping it over a line of reflection (generally a mirror).
Distance of the image of a point from a line of reflection = Distance of the original point from that line of reflection
If a point lies exactly on the line of reflection, then the image of that point will form at the same place where the original point is situated.
That is, Distance of the image of a point from a line of reflection = Distance of the original point from that line of reflection = 0
Reflections in the Coordinate plane
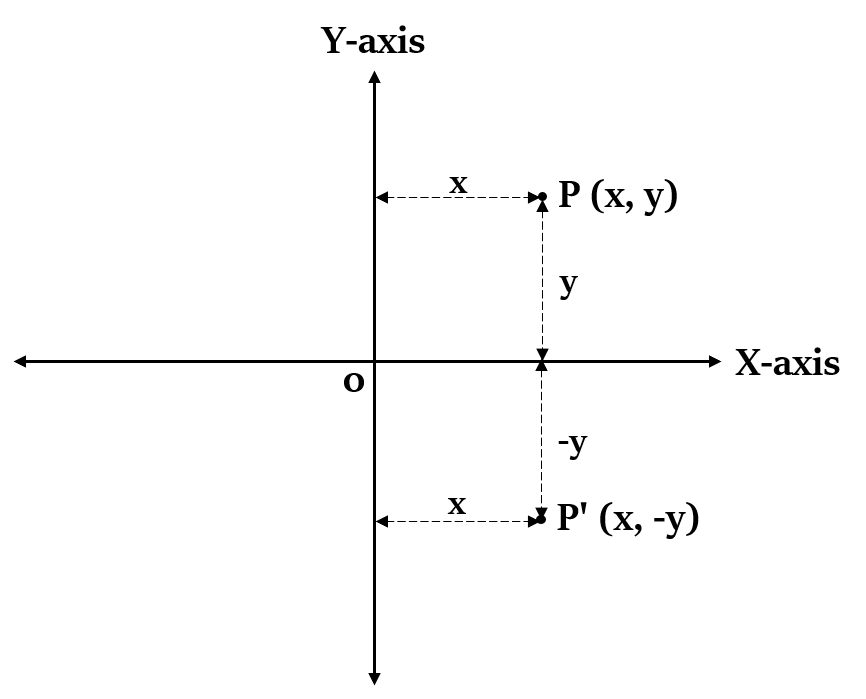
Reflection of a point P(x, y) on X-axis
If a point P(x, y) is reflected over the X-axis (i.e. y = 0), then the ccordinates of its image P’ will be (x, -y).
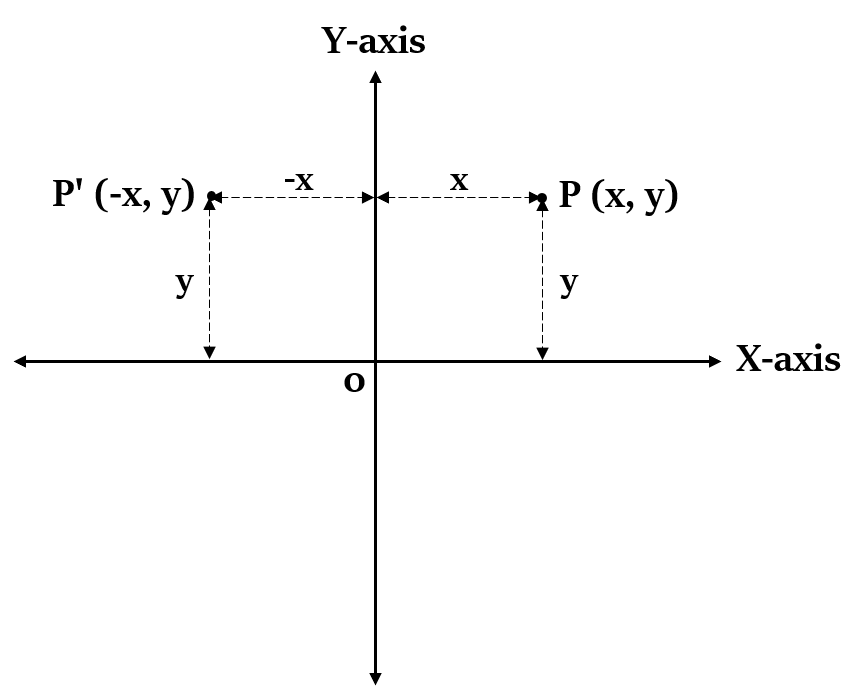
Reflection of a point P(x, y) over the line y = b
If a point P(x, y) is reflected over the line y = b (where b is a constant), then the ccordinates of its image P’ will be (x, 2b - y).
Reflection of a point P(x, y) on Y-axis
If a point P(x, y) is reflected over the Y-axis (i.e. x = 0), then the ccordinates of its image P’ will be (-x, y).
Reflection of a point P(x, y) over the line x = a
If a point P(x, y) is reflected over the line x = a (where a is a constant), then the ccordinates of its image P’ will be (-x + 2a, y).
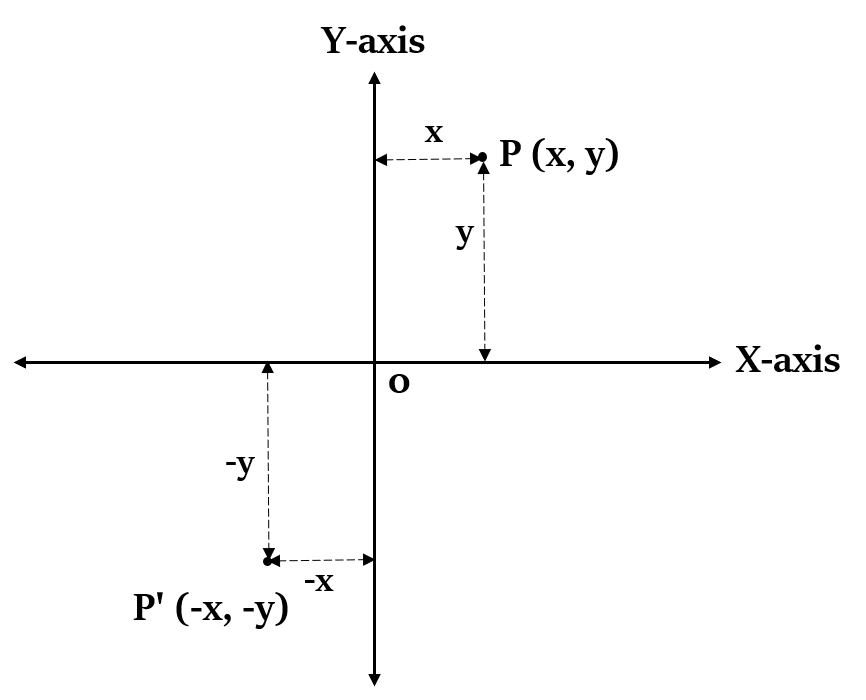
Reflection of a point P(x, y) over the Origin
If a point P(x, y) is reflected over the origin (0, 0), then the ccordinates of its image P’ will be (-x, -y).
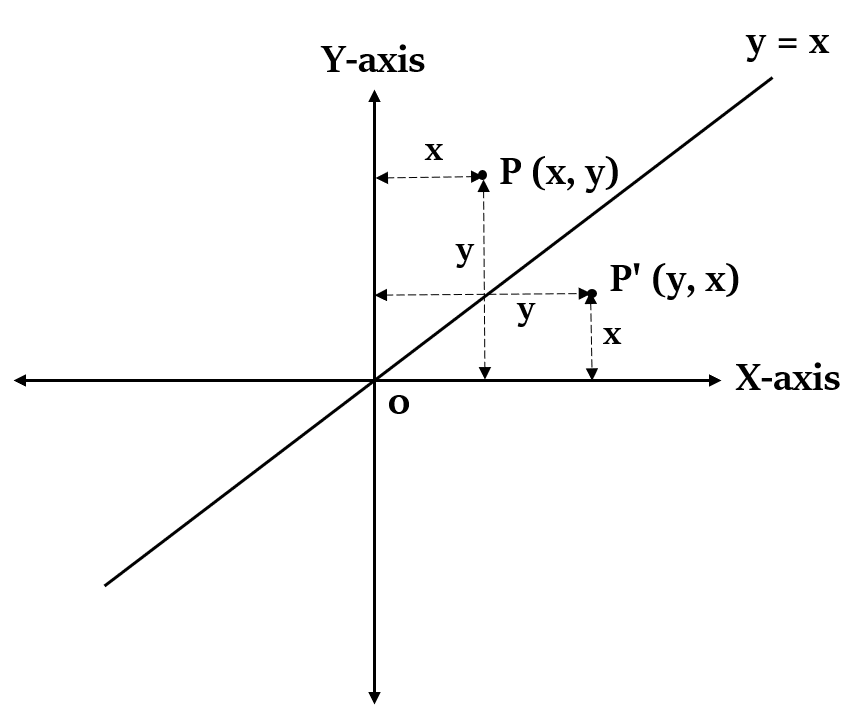
Reflection of a point P(x, y) over the line y = x
If a point P(x, y) is reflected over the line y = x, then the ccordinates of its image P’ will be (y, x).
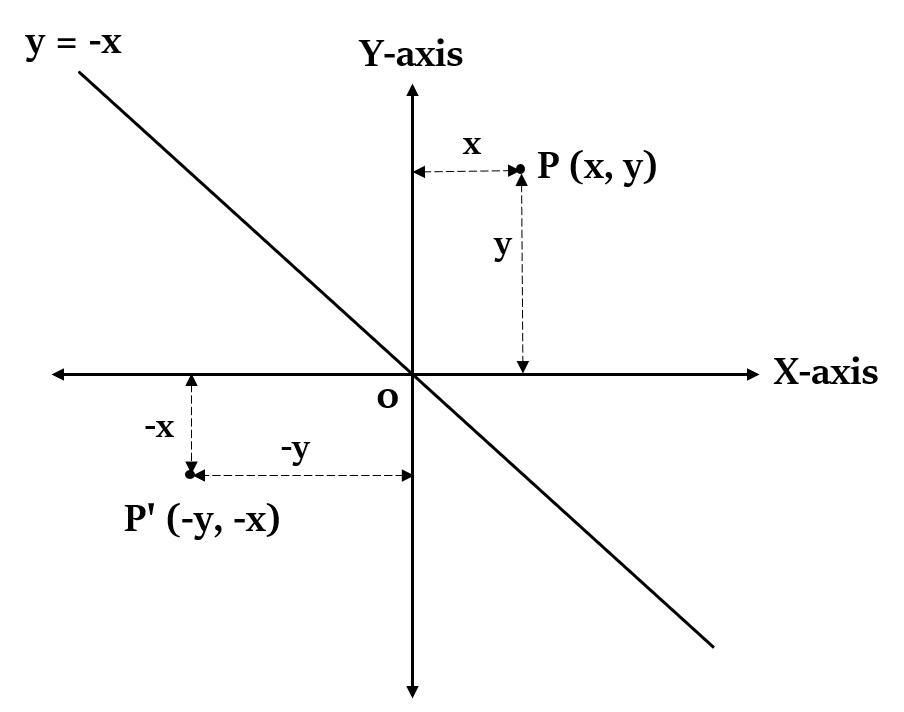
Reflection of a point P(x, y) over the line y = -x
If a point P(x, y) is reflected over the line y = -x, then the ccordinates of its image P’ will be (-y, -x).
Summary
Here’s a table summarizing the above points.
| Line or Point of Reflection | Coordinates of Original Point | Coordinates of Image |
|---|---|---|
| X-axis (y = 0) | P(x, y) | P'(x, -y) |
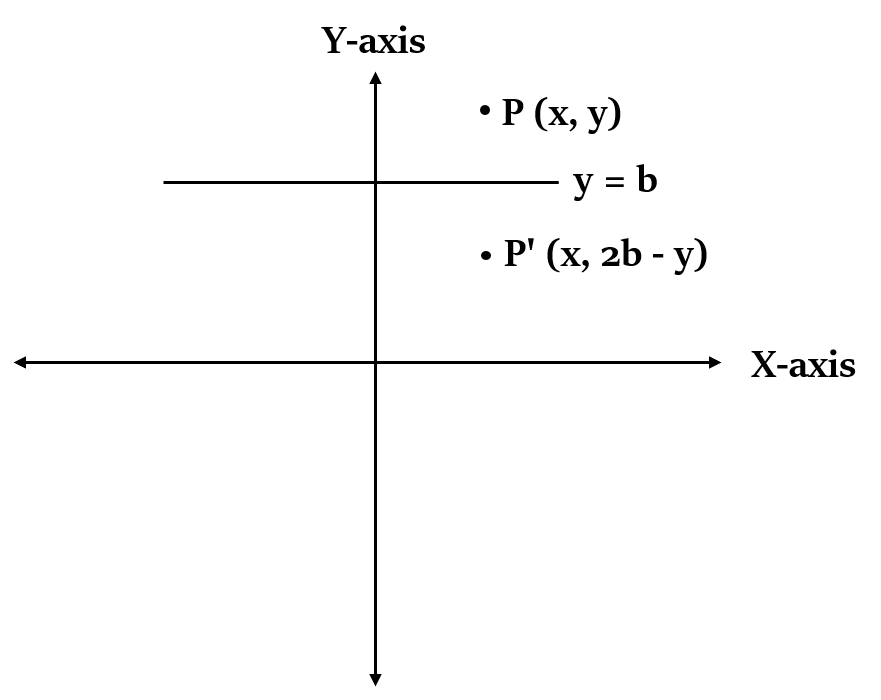
| y = b | P(x, y) | P'(x, 2b - y) |
| Y-axis (x = 0) | P(x, y) | P'(-x, y) |
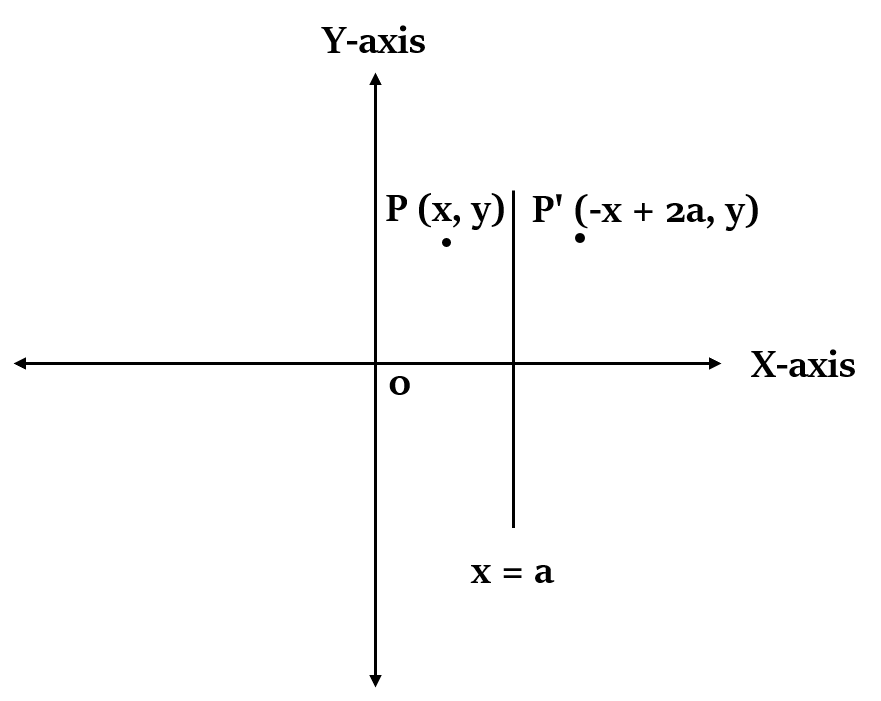
| x = a | P(x, y) | P'(-x + 2a, y) |
| Origin (0, 0) | P(x, y) | P'(-x, -y) |
| y = x | P(x, y) | P'(y, x) |
| y = -x | P(x, y) | P'(-y, -x) |