Coordinate Geometry - Finding Coordinates and Position of points
In this article, we will learn how to use the concepts of Coordinate Geometry in case of points.
Position of a point with respect to a line
We can easily find out whether given two points are on the same side of a line or on opposite sides. Let’s see how.
If A ($x_1$, $y_1$) and B ($x_2$, $y_2$) are two points and equation of a line is ax + by + c = 0, then:
Those two points will be on the same side of the line, if:
$(ax_1 + by_1 + c)$ and $(ax_2 + by_2 + c)$ have the same signs.
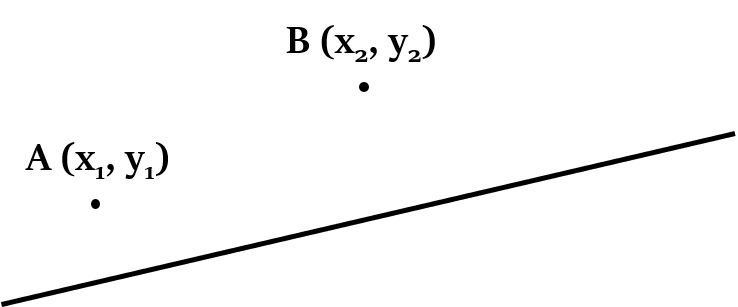
Those two points will be on the opposite sides of the line, if:
$(ax_1 + by_1 + c)$ and $(ax_2 + by_2 + c)$ have opposite signs.
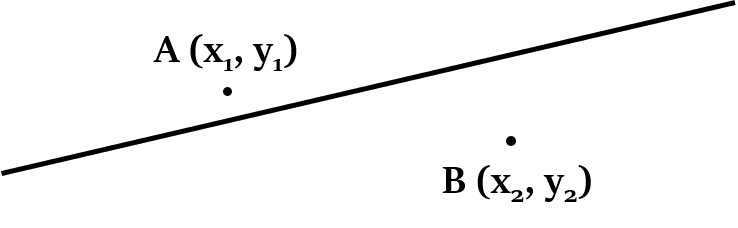
Finding Coordinates of a point dividing a line
If we know the ratio in which a point divides a line internally or externally, we can find the coordinate of that point.
Internal division of a line segment
If a point A (x, y) divides the line joining two points P (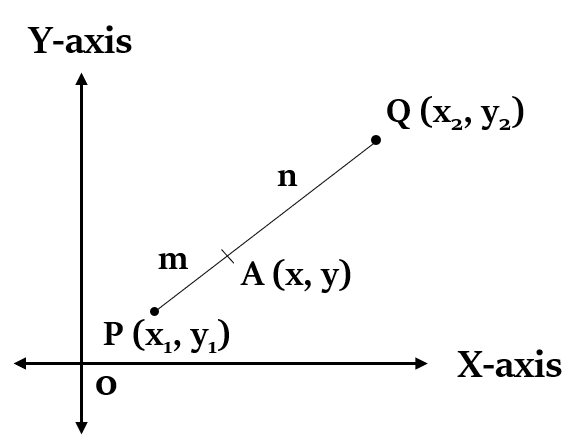$x_1$, $y_1$) and Q ($x_2$, $y_2$) internally, in the ratio m:n, then:
x = $\frac{m x_2 + n x_1}{m + n}$
y = $\frac{m y_2 + n y_1}{m + n}$
Speacial Case
In case of the mid-point of a line segment, m:n = 1:1
So, coordinates of the mid-point of a line segment joining two points P ($x_1$, $y_1$) and Q ($x_2$, $y_2$), will be:
x = $\frac{x_2 + x_1}{2}$
y = $\frac{y_2 + y_1}{2}$
External division of a line segment
If a point A (x, y) divides the line joining two points P (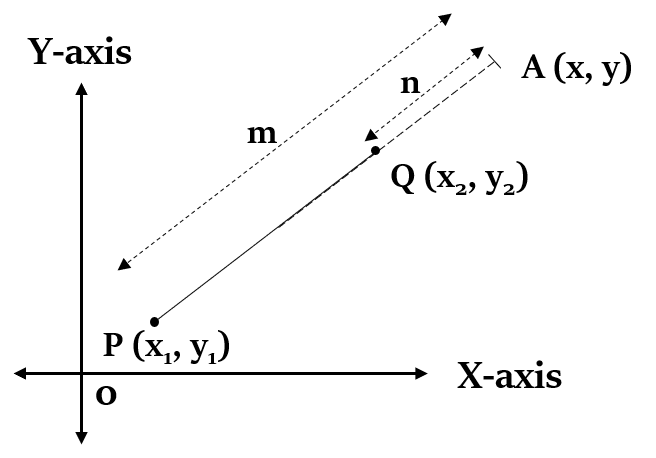$x_1$, $y_1$) and Q ($x_2$, $y_2$) externally, in the ratio m:n, then:
x = $\frac{m x_2 - n x_1}{m - n}$
y = $\frac{m y_2 - n y_1}{m - n}$
Distance between two Coordinates
We can find distance between two points, if we know their coordinates.
If we have two points on a Cartesian plane, P (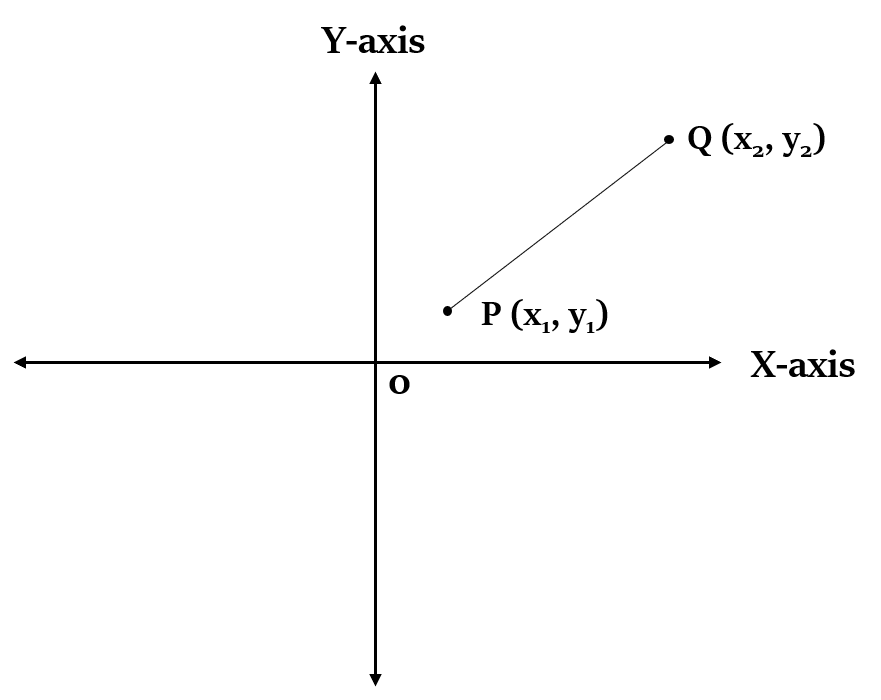$x_1$, $y_1$) and Q ($x_2$, $y_2$), then:
Distance between P and Q, d = $\sqrt{(x_1 - x_2)^2 + (y_1 - y_2)^2}$
Special Case
Distance between a point P (x, y) and the origin (0, 0) = $\sqrt{(x - 0)^2 + (y - 0)^2}$ = $\sqrt{x^2 + y^2}$
Minimum distance of a point from a straight line
Minimum distance of a point from a straight line = Length of the perpendicular dropped from that point on that line.
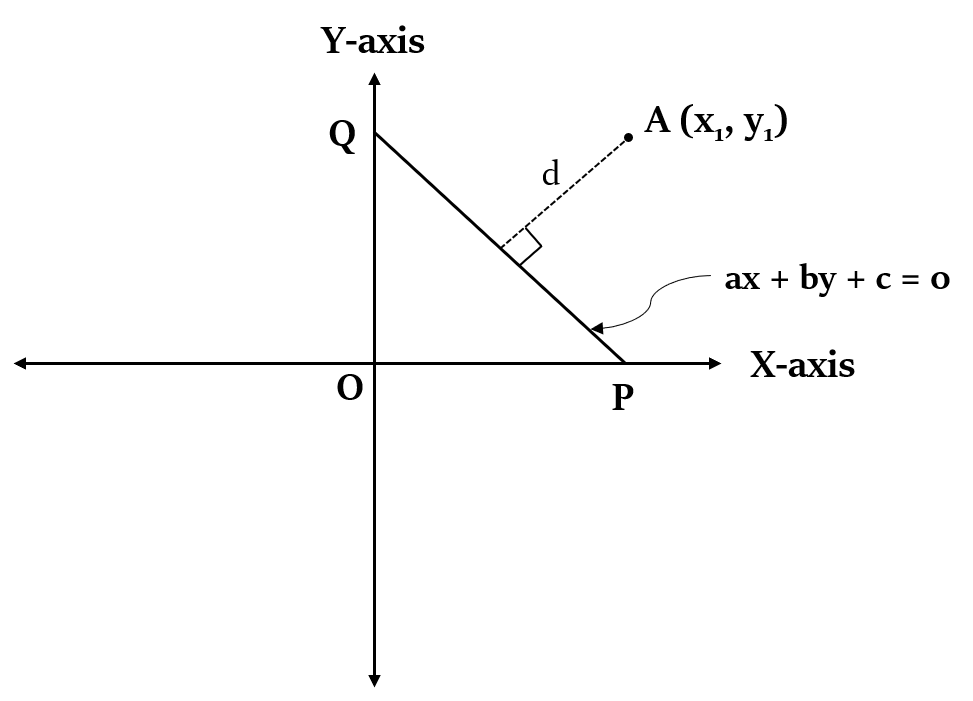
The length of perpendicular from a given point ($x_1, y_1$) to a line ax + by + c = 0 can be calculated using the following formula:
d = $\frac{|a x_1 + b y_1 + c|}{\sqrt{a^2 + b^2}}$
The length of perpendicular from the origin (0, 0) to a line ax + by + c = 0 is given by the following formula:
d = $\frac{|c|}{\sqrt{a^2 + b^2}}$
Finding Collinear points
Three given points (say A, B and C) are collinear (i.e. they lie on the same straight line) if anyone of the following conditions is met:
- Area of the ∆ABC is zero.
- Slope of lines joining any two given points is the same. That is, Slope of AB = Slope of BC = Slope of CA.
- If the sum of the lengths of any two line segments is equal to the third line segment. Say, if AB + BC = AC