Concept of Opposite faces
There are 6 faces in the dice and every face has an opposite face.
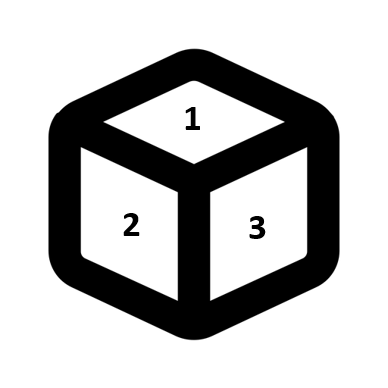Three faces are visible, while three are invisible if one position of dice is given.
Finding Opposite Face - When Single Position of a Dice is Given
From a single position of a dice we may tell for sure sometimes that a given dice is a general dice, but we can never tell for sure that a given dice is a standard dice. So, we can never tell the opposite face of any face in such a case.
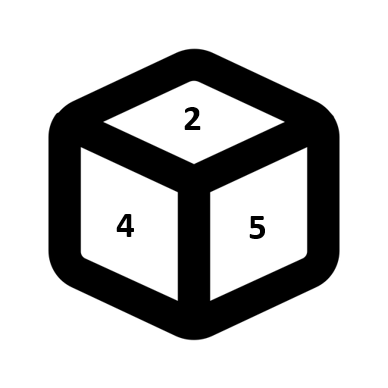
Q. What will be the digit on the opposite face of the particular face having digit 4 in the dice given below?
Explanation:
2 and 5 cannot be on the opposite face of 4 as they are adjacent to it. So, number opposite to 4 can be any number from 1, 3 and 6. So, the answer will be 1/3/6.
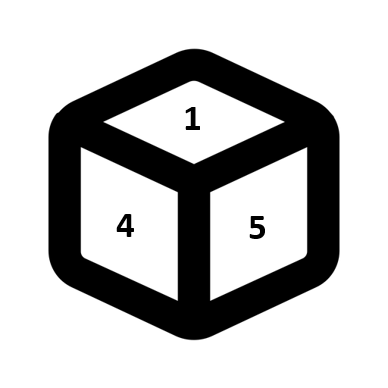
Q. What will be the digit on the opposite face of the particular face having digit 4 in the dice given below?
Explanation:
Clearly, the sum of the digits on the adjacent faces is not equal to 7. Hence, the given dice may be a standard dice or a general dice. Opposite face to 4 may be 2, 3 or 6.
When only one position of a dice is given, we cannot determine with surety that a given dice is a standard dice (until and unless it’s explicitly mentioned). Hence, we will assume it to be a general dice and any of the 3 invisible faces may lie opposite to any of the visible faces.
In some questions, the answer options may not contain all the possible numbers which can exist on the opposite side of a given number. Then, the correct answer is the option containing maximum possible correct numbers.
But we may find the exact opposite face in a few cases even when only one position of dice is given.
Q. In a dice a, b, c and d are written on the adjacent faces, in a clockwise order and e and f at the top and bottom. When c is at the top, what will be at the bottom?
(a) a (b) b (c) c (d) d
Explanation:
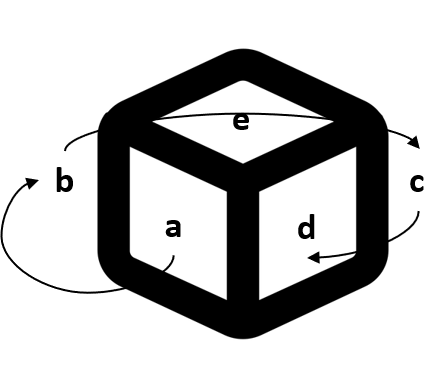Clearly, a is opposite to c. So, when c will be at the top, then a will be at the bottom.Answer: (a)
So, we were able to find the exact opposite face even when only one position of the dice was given, because the question provided us a lot of information in language form.
Finding Opposite Face - When Two Positions of a Dice are Given
When two positions of the same dice are given then four possible cases emerge:
- All three faces are the same - In such case we cannot find the exact opposite face.
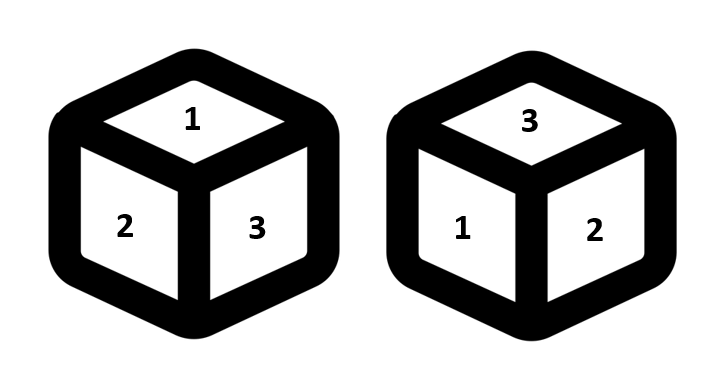It’s as good as giving one position of the dice. Only three unique faces are visible to us. So no pairing possible. In such case any of the three invisible digits can be opposite to any of the three visible digits. - No face is same, i.e. all three faces are different - In such case too, we cannot find the exact opposite face.
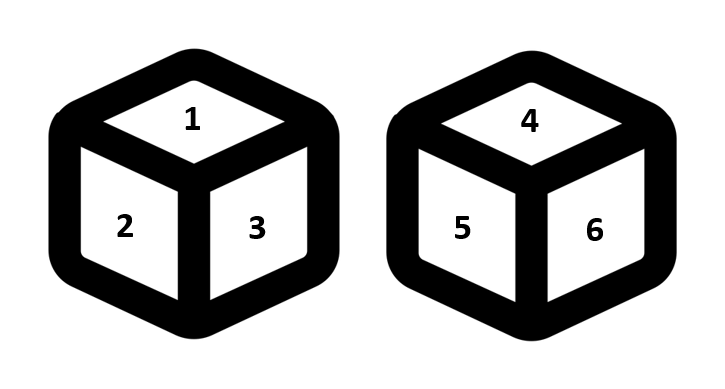All six unique faces are visible to us. But no relation given, i.e. all the digits are different from one another. So no pairing possible. In such case any digit in position I can be opposite to any of the three digits in position II. - Two faces are same - we can find the opposite face.
- One face is same - we can find the opposite face.
So, we can find the opposite faces if one or two faces are same in the given two positions of the dice. Let’s see how to do so.
When two digits are common
For example, see the following two positions of a dice:
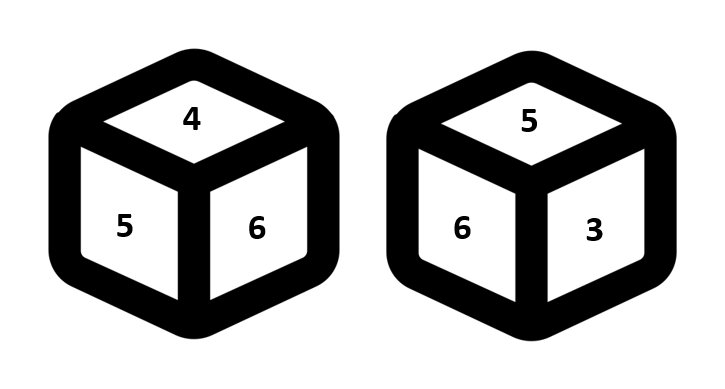Only four unique faces are visible to us, i.e. 3, 4, 5 and 6. So, only one pairing is possible.
5 and 6 are visible in both the positions, i.e. they are common. In such cases uncommon digits in each dice are opposite to each other, i.e. 4 and 3 are opposite to each other.
Any of the two invisible digits may be present on the faces opposite to the faces having common digits, i.e. either 1 or 2 may lie opposite to 5 and 6.
Q. In the following question the two positions of a single dice are given. Find the digit on the face which is opposite to the face having digit 2.
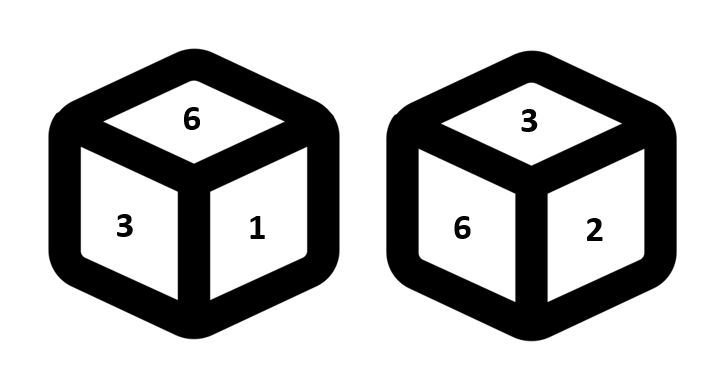
(a) 4 (b) 5 (c) 1 (d) Cannot be determined
Explanation:
Answer: (c)
When one digit is common
For example, see the following two positions of a dice:
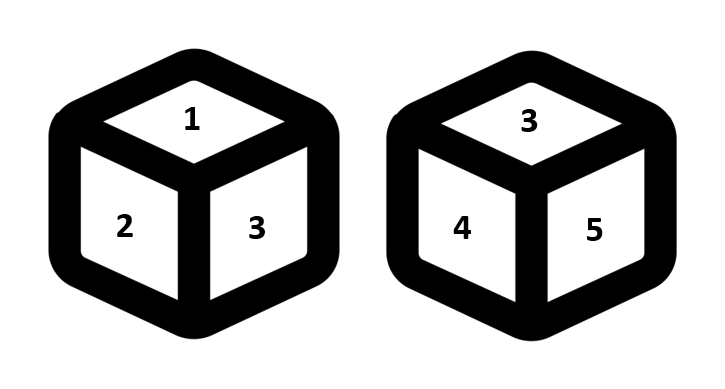Five unique faces are visible to us, i.e. 1, 2, 3, 4 and 5. So, all the opposite faces may be paired.
In such cases we can apply the clockwise/anti-clockwise rule. In this case we start from the common digit and move in clockwise (or anti-clockwise) direction. So, we will start moving from digit 3 in both the dices.
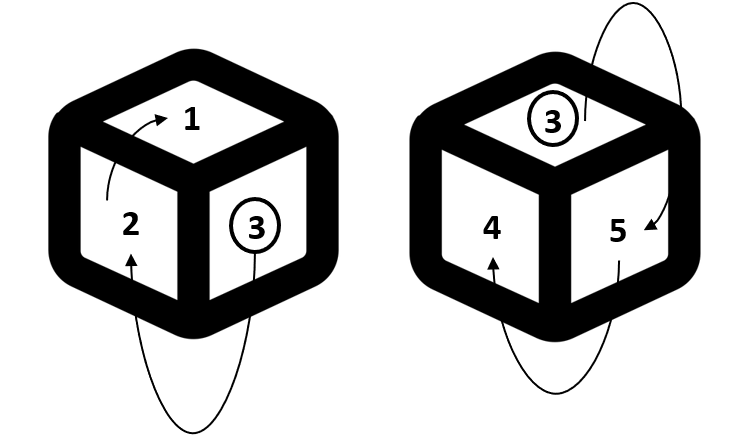The first digits we encounter in the two dices will be opposite to each other (i.e. 2 and 5). Similarly, on moving further, the second digits we encounter in the two dices will be opposite to each other (i.e. 1 and 4). The common digit, from where we started moving, will be opposite to the digit which is not visible (i.e. 3 and 6).Q. In the following question, two positions of a single dice are given. Find the face which is opposite to the face having digit 6.
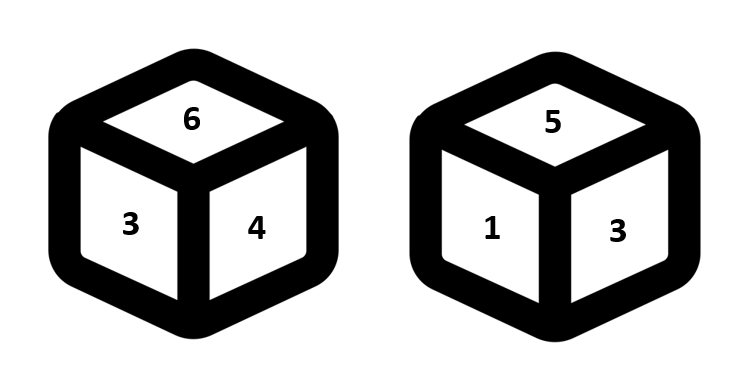
(a) 5 (b) 1 (c) 2 (d) 3
Explanation:
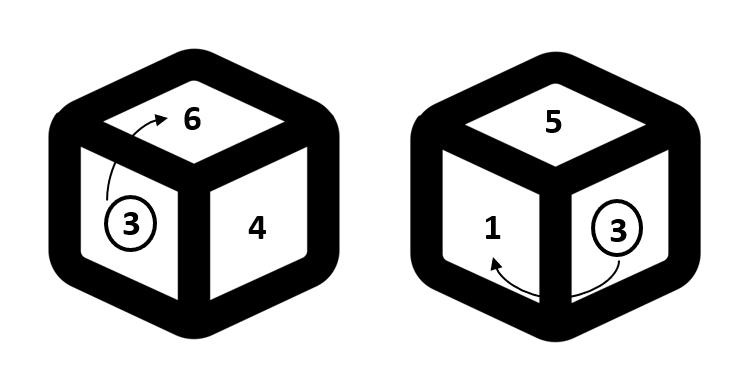Starting clockwise from 3, we can clearly see that 6 and 1 are opposite to each other.
Answer: (b)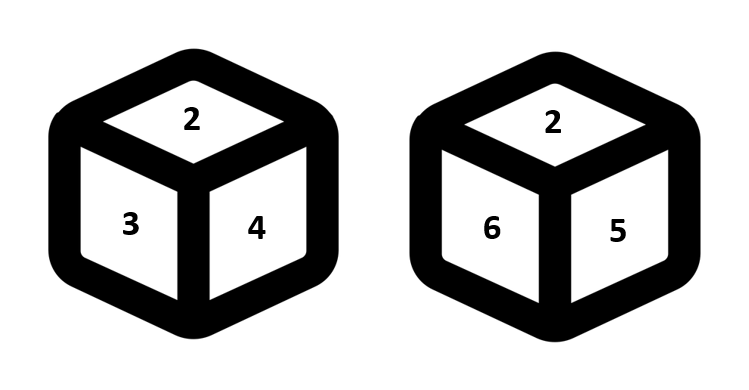
In such cases the corresponding faces of the two dices will be opposite to each other (i.e. 3-6 and 4-5), and the common digit will obviously be opposite to the invisible face (i.e. 2-1).We will get the same answer even if we apply the clockwise rule.