Concept of Base Change
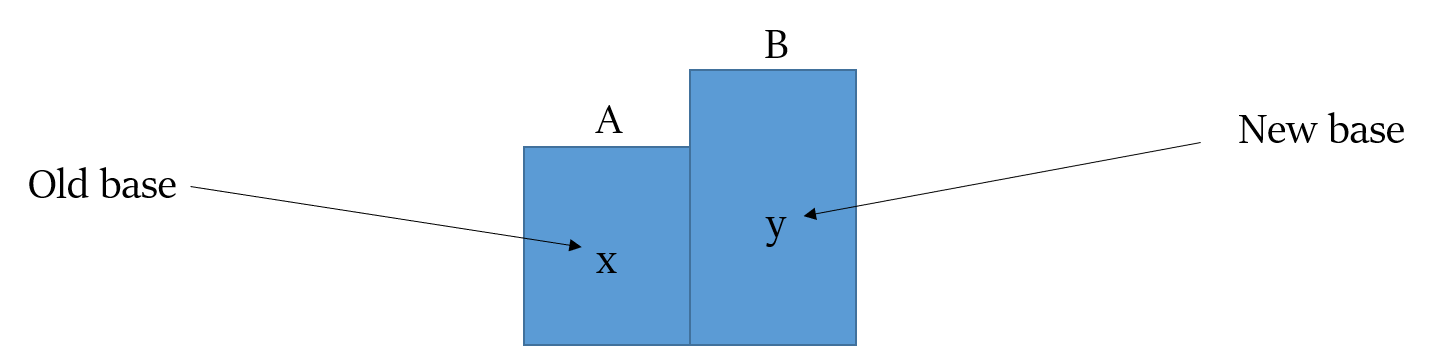
Question types covered:
Percent Change Reversal – If x is increased/decreased to y, then by what percent should y be decreased/increased to take it back to the original value?
If B is p% more/less than A, then A is how much percent less/more than B?
If z = x × y, and x is increased/decreased by p%, then by what percentage y should be decreased/increased to maintain the same value of z?
Traditional method
Using the variables.
Q. If salary of Mragank is 20% more than the salary of Aanya, then the salary of Aanya is how much percent less than the salary of Mragank?
Explanation:
Let Salary of Aanya be x.
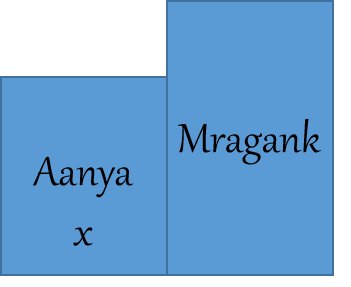 Mragank is 20% more than the salary of Aanya.
Mragank is 20% more than the salary of Aanya.So, Salary of Mragank = x + (20/100) × x = 1.2 x
Difference is salaries remain the same, i.e. 0.2x.
Required percentage = (0.2x/1.2x) × 100 = (1/6) × 100 = 16.67%
Formula Method
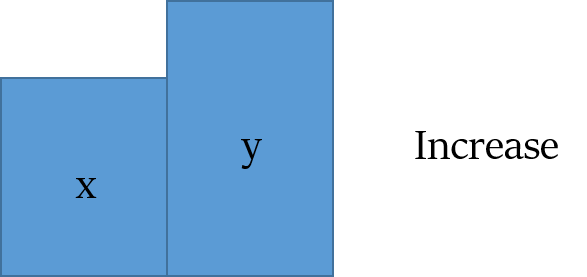 If a value x is increased by p%, then to get back to the original x, we have to decrease the increased value by
If a value x is increased by p%, then to get back to the original x, we have to decrease the increased value by OR
If y is p% more than x, then x is
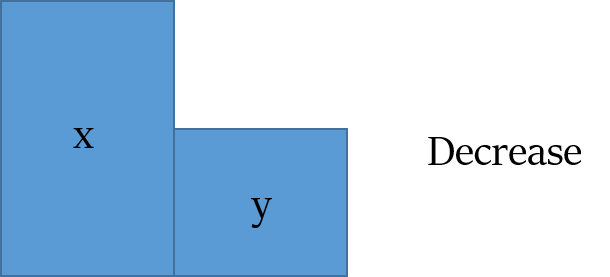 If a value x is decreased by p%, then to get back to the original x, we have to increase the decreased value by
If a value x is decreased by p%, then to get back to the original x, we have to increase the decreased value by OR
If y is p% less than x, then x is
Q. If salary of Mragank is 20% more than the salary of Aanya, then the salary of Aanya is how much percent less than the salary of Mragank?
Explanation:
If y is p% more than x, then x is
So, Required percentage = (20/120) × 100 = (1/6) × 100 = 16.67%
Percentage Method
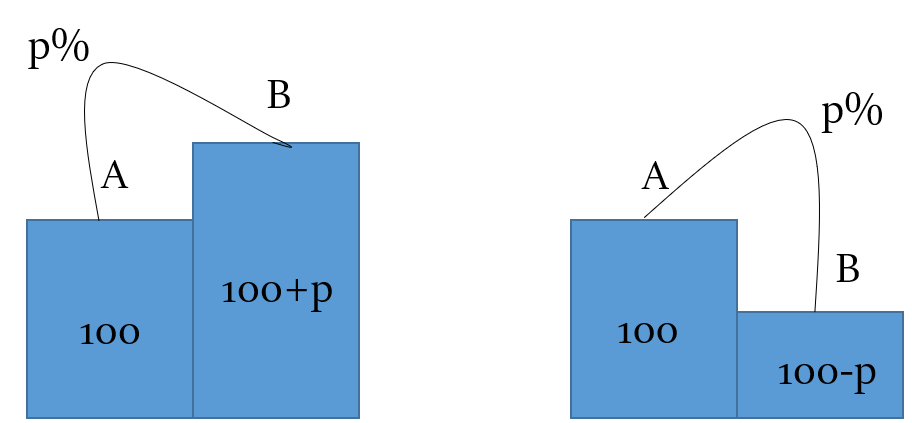
Q. If salary of Mragank is 20% more than the salary of Aanya, then the salary of Aanya is how much percent less than the salary of Mragank?
Explanation:
Salary of Mragank is 20% more than the salary of Aanya. - Base is the salary of Aanya.
If Aanya’s salary = 100, then Mragank’s salary = 120
 Salary of Aanya is how much percent less than the salary of Mragank. - Now, Base is the salary of Mragank.
Salary of Aanya is how much percent less than the salary of Mragank. - Now, Base is the salary of Mragank.Difference is salaries remain the same, i.e. 20. But now base will be 120.
Required percentage = (20/120) × 100 = (1/6) × 100 = 16.67%
Fraction Method

Increase: In terms of fraction, if a value x is first increased by p% (= n/d) then to get back to the original number x, we have to decrease the increased value by
Decrease: In terms of fraction, if a value x is first decreased by p% (= n/d) then to get back to the original number x, we have to increase the increased value by
For example, a number is increased by 25%
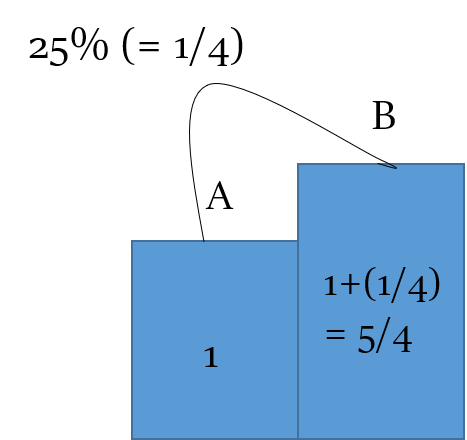 25% = 𝒏/𝒅 = 𝟏/𝟒 - It implies an increase of 1 on 4
25% = 𝒏/𝒅 = 𝟏/𝟒 - It implies an increase of 1 on 4
So, the original number ≡ 4 (i.e. d)
And new number ≡ 4 + 1 = 5 (i.e. d + n)
Percent change required in bringing down 5 to 4 again = 1/5 ≡ 20%
On the other hand, if a number is decreased by 25%
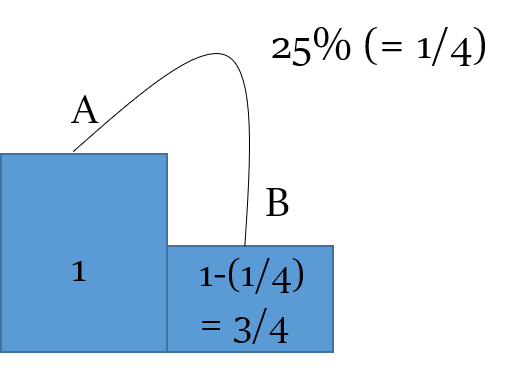 25% = 𝒏/𝒅 = 𝟏/𝟒 - It implies an decrease of 1 on 4
25% = 𝒏/𝒅 = 𝟏/𝟒 - It implies an decrease of 1 on 4
So, the original number ≡ 4 (i.e. d)
And new number ≡ 4 - 1 = 3 (i.e. d - n)
Percent change required in bringing up 3 to 4 again = 1/3 ≡ 33.33%
Q. If salary of Mragank is 20% more than the salary of Aanya, then the salary of Aanya is how much percent less than the salary of Mragank?
Explanation:
20% is equivalent to 1/5
If Aanya’s salary = 5, then Mragank’s salary = 6
 Difference is salaries remain the same, i.e. 1. But now base will be 6.
Difference is salaries remain the same, i.e. 1. But now base will be 6.Required percentage = 1/6 × 100 = 16.67%
Q. If salary of Mragank is 20% less than the salary of Aanya, then the salary of Aanya is how much percent more than the salary of Mragank?
Explanations :
If y is p% less than x, then x is
So, Required percentage = (20/80) × 100 = (1/4) × 100 = 25%
Percentage Method or Fraction Method?
Should we use the Percentage Method or Fraction Method?
Let us try to understand it using a couple of examples.
Q. On increasing a number by 37.5%, the new number obtained is 63 more than the original number. What must be the original number?
Explanations :
37.5% is equivalent to 63
So, 37.5% ≡ 63
Then, 100% ≡ 63 × 100/37.5 = 63 × 8/3 = 21 × 8 = 168
Complex calculation involved!
Q. On increasing a number by 37.5%, the new number obtained is 231. What must be the original number?
Explanations :
137.5% (i.e. 100 + 37.5%) is equivalent to 231
So, 137.5% ≡ 231
Then, 100% ≡ 231 × 100/(100+37.5) = 231 × 100/137.5 = 231 × 8/11 = 21 × 8 = 168
Complex calculation involved!
As you will keep on practicing you will develop a better sense of which method to use based on the kind of data given in the question.
 Salary of Aanya is how much percent more than the salary of Mragank. - Now, Base is the salary of Mragank.
Salary of Aanya is how much percent more than the salary of Mragank. - Now, Base is the salary of Mragank.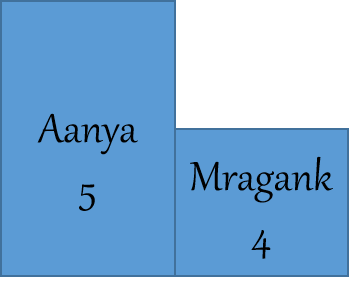 Difference is salaries remain the same, i.e. 1. But now base will be 4.
Difference is salaries remain the same, i.e. 1. But now base will be 4.