Concept of Percent Change
Percent Change
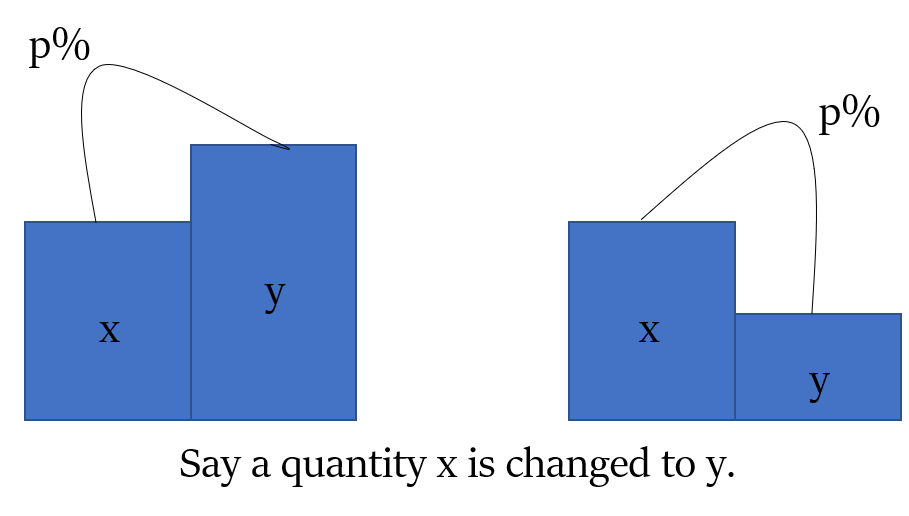Here base is xPercentage Change (increase or decrease) in a quantity,
p% = $\frac{Change \hspace{1ex} in \hspace{1ex} quantity}{Original \hspace{1ex} quantity}$ × 100% = $\frac{y − x}{x}$ × 100%
p% = $\frac{Change \hspace{1ex} in \hspace{1ex} quantity}{Original \hspace{1ex} quantity}$ × 100% = $\frac{y − x}{x}$ × 100%
Q. If price of sugar increases from Rs 18/kg to Rs 30/kg, then what is the percent increase?
Explanation:
Change in price = 30 – 18 = Rs 12 (Plus sign denotes an increase)
So, Percent change = $\frac{Change \hspace{1ex} in \hspace{1ex} quantity}{Original \hspace{1ex} quantity}$ × 100%
= ($\frac{12}{18}$ × 100)% = ($\frac{2}{3}$ × 100)% = 66.67%
(Plus sign denotes a percentage increase)
So, Percent change = $\frac{Change \hspace{1ex} in \hspace{1ex} quantity}{Original \hspace{1ex} quantity}$ × 100%
= ($\frac{12}{18}$ × 100)% = ($\frac{2}{3}$ × 100)% = 66.67%
(Plus sign denotes a percentage increase)
Q. If price of sugar decreases from Rs 25/kg to Rs 15/kg, then what is the percent decrease?
Explanation:
Change in price = 15 – 25 = Rs -10 (Minus sign denotes a decrease)
So, Percent change = $\frac{Change \hspace{1ex} in \hspace{1ex} quantity}{Original \hspace{1ex} quantity}$ × 100%
= ($\frac{-10}{25}$ × 100)% = ($\frac{-2}{5}$ × 100)% = -40%
(Minus sign denotes a percentage decrease)
So, Percent change = $\frac{Change \hspace{1ex} in \hspace{1ex} quantity}{Original \hspace{1ex} quantity}$ × 100%
= ($\frac{-10}{25}$ × 100)% = ($\frac{-2}{5}$ × 100)% = -40%
(Minus sign denotes a percentage decrease)
Finding new quantity
When a quantity x is increased/decreased by p%, then:
New quantity, y = Base ± Absolute change in Base
= x ± p% of x = x ± x(p/100) = x (1 ± p/100)
Concept of Multiplying Factor
New quantity, y = x ± p% of x = x (1 ± p%)
So, Multiplying factor : (1 ± p%)
Multiplying Factor is the same as (1 + p/100) for p% increase
E.g. Multiplying Factor for 15% increase = 1.15
Multiplying Factor for 8% increase = 1.08Multiplying Factor is the same as (1 - p/100) for p% decrease
Multiplying Factor for 35% decrease = 0.65
Multiplying Factor for 5% decrease = 0.95
Q. If 60 is increased by 25%, find the new number.
Explanations :
Explanation 1:
Here base is the number itself, i.e. 60
So, new number = original number (i.e. our base) + Percentage increase over this base
So, new number = 60 + 25% of 60
So, new number = 60 + 15 = 75
Here base is the number itself, i.e. 60
So, new number = original number (i.e. our base) + Percentage increase over this base
So, new number = 60 + 25% of 60
So, new number = 60 + 15 = 75
Explanation 2: Using the concept of Multiplying Factors
Here base is the number itself, i.e. 60
So, new number = original number (i.e. our base) × Multiplying Factor
Multiplying Factor = 1 + p% = 1 + 25% = 1 + 0.25 = 1.25
So, new number = 60 × 1.25 = 75
Here base is the number itself, i.e. 60
So, new number = original number (i.e. our base) × Multiplying Factor
Multiplying Factor = 1 + p% = 1 + 25% = 1 + 0.25 = 1.25
So, new number = 60 × 1.25 = 75
Q. If 60 is decreased by 25%, find the new number.
Explanations :
Explanation 1:
Here base is the number itself, i.e. 60
So, new number = original number (i.e. our base) - Percentage decrease over this base
So, new number = 60 - 25% of 60
So, new number = 60 - 15 = 45
Here base is the number itself, i.e. 60
So, new number = original number (i.e. our base) - Percentage decrease over this base
So, new number = 60 - 25% of 60
So, new number = 60 - 15 = 45
Explanation 2: Using the concept of Multiplying Factors
Here base is the number itself, i.e. 60
So, new number = original number (i.e. our base) × Multiplying Factor
Multiplying Factor = 1 - p% = 1 - 25% = 1 - 0.25 = 0.75
So, new number = 60 × 0.75 = 45
Here base is the number itself, i.e. 60
So, new number = original number (i.e. our base) × Multiplying Factor
Multiplying Factor = 1 - p% = 1 - 25% = 1 - 0.25 = 0.75
So, new number = 60 × 0.75 = 45
Q. By how much percent is 36 more than 27?
Explanations :
Explanation 1:
Here base is 27
Difference = 36 – 27 = 9
Required percentage = (9/27) × 100 = 1/3 × 100 = 33.33%
Here base is 27
Difference = 36 – 27 = 9
Required percentage = (9/27) × 100 = 1/3 × 100 = 33.33%
Explanation 2: Using the concept of Multiplying Factors
Here base is 27
36/27 = 4/3 = 1.33
Multiplying Factor = 1.33, which is equivalent to 33% increase.
So, 36 is 33.33% more than 27.
Here base is 27
36/27 = 4/3 = 1.33
Multiplying Factor = 1.33, which is equivalent to 33% increase.
So, 36 is 33.33% more than 27.
Q. By how much percent is 40 less than 60?
Explanations :
Explanation 1:
Here base is 60
Difference = 60 – 40 = 20
Required percentage = (20/60) × 100 = 1/3 × 100 = 33.33%
So, 40 is 33.33% less than 60.
Here base is 60
Difference = 60 – 40 = 20
Required percentage = (20/60) × 100 = 1/3 × 100 = 33.33%
So, 40 is 33.33% less than 60.
Explanation 2: Using the concept of Multiplying Factors
Here base is 60
40/60 = 2/3 = 0.67
Multiplying Factor = 0.67, which is equivalent to 33% decrease.
So, 40 is 33.33% less than 60.
Here base is 60
40/60 = 2/3 = 0.67
Multiplying Factor = 0.67, which is equivalent to 33% decrease.
So, 40 is 33.33% less than 60.
Q. Two numbers are 12.5% and 25% more than a third number respectively. The first number must be how much percent more/less than the second number?
Explanation :
Let the third number be 100.
Then, first number = 100 + 12.5% of 100 = 112.5
And, second number = 100 + 25% of 100 = 125
Required percentage = (12.5/125) × 100 = 10% (less)
Then, first number = 100 + 12.5% of 100 = 112.5
And, second number = 100 + 25% of 100 = 125
Required percentage = (12.5/125) × 100 = 10% (less)