Divisibility

Concept of Divisibility

A and B are two integers (either positive or negative), such that B ≠ 0

If A/B is an integer, then we can say that A is divisible by B (or A is a multiple of B).

E.g. if A = 18 and B = 3, then 18/3 = 6. So, 18 is divisible by 3.

Divisibility Rule

Divisibility rule – to find out whether a number is divisible by another number without actually performing the division. This is done by examining their digits.

There are two basic things that we need to keep in mind while finding out whether a number is divisible by another number:

• If the divisor is a prime number: We just need to apply the divisibility rule for that number.
  
  E.g. Is 215 divisible by 5?
  5 is a prime number. So, we just need to apply the divisibility rule for 5.

• If the divisor is a composite number: We need to find co-prime factors of the divisor and then apply the divisibility rule for each such factor. The number will be divisible by the divisor, if it is divisible by all these co-prime factors.
  
  E.g. Is 156 divisible by 12?
  12 = 4 × 3
  4 and 3 are co-prime numbers. So, we just need to apply the divisibility rule for 4 and 3 now.

Divisibility Rule for 5, 10

A number is divisible by 5 if its unit’s digit is either 0 or 5.

E.g. 310 and 465 are divisible by 5.
311 and 464 are not divisible by 5.

A number is divisible by 10 if its unit’s digit is 0.

E.g. 310 and 460 are divisible by 10.
611 and 564 are not divisible by 10.

Divisibility Rule for 2, 4, 8, 16

A number is divisible by 2 if its unit’s digit is 0, 2, 4, 6, or 8, i.e. if the unit digit is divisible by 2.

E.g. 124 is divisible by 2, as 4 is divisible by 2.
613 is not divisible by 2, as 3 is not divisible by 2.

A number is divisible by 4 if the number formed by its last two digits is divisible by 4.

E.g. 124 is divisible by 4, as 24 is divisible by 4.
613 is not divisible by 4, as 13 is not divisible by 4.

A number is divisible by 8 if the number formed by its last three digits is divisible by 8.

E.g. 124 is divisible by 8, as 24 is divisible by 8.
613 is not divisible by 8, as 13 is not divisible by 8.

A number is divisible by 16 if the number formed by its last four digits is divisible by 16.

E.g. 5112 is divisible by 16, as 112 is divisible by 16.
6415 is not divisible by 16, as 415 is not divisible by 16.

Divisibility Rule for 3, 9

A number is divisible by 3, if sum of its digits is divisible by 3.

E.g. 123 is divisible by 3, as (1 + 2 + 3 = 6) is divisible by 3.
1363 is not divisible by 3, as (1 + 3 + 6 + 3 = 13) is not divisible by 3.

A number is divisible by 9, if sum of its digits is divisible by 9.

E.g. 126 is divisible by 9, as (1 + 2 + 6 = 9) is divisible by 9.
123 is not divisible by 9, as (1 + 2 + 3 = 6) is not divisible by 9.

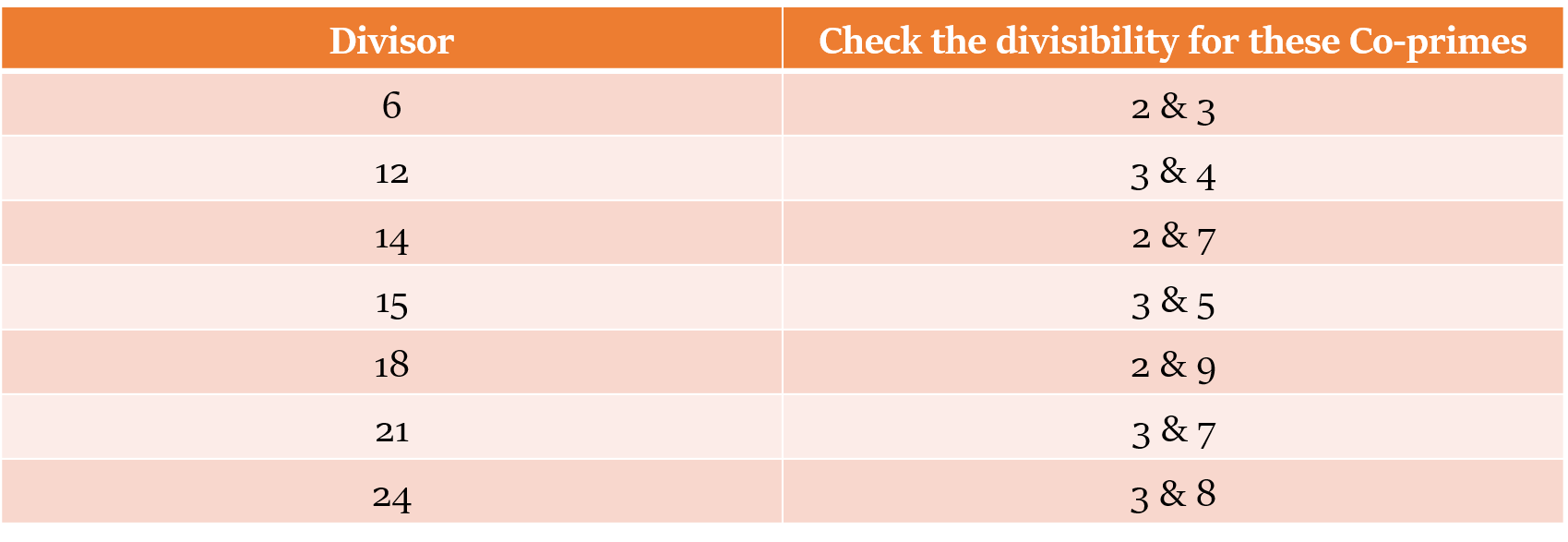
Divisibility by 6, 12, 14, 15, 18, 21, etc.

For these composite numbers, we will use Co-prime factor method.

To check whether a given number is divisible by 6, 12, 14, 15, 18, 21 etc, we need to check whether the given number is divisible by the co-prime factors of these divisors.

If a number is divisible by x as well as y (where x and y are co-primes), then the given number is divisible by xy.

Example: 6 = 2 x 3. So, any number that is divisible by 2 and 3 will be divisible by 6 too.
E.g. 186 is divisible by both 2 and 3, hence 186 is divisible by 6.

Divisibility by 7, 13, 17, 19 and 23

To check divisibility by these prime numbers (7, 13, 17, 19 and 23), we will use Operator and Operation based method.

Everyone of these divisors has a specific operator and a specific operation. It has been shown in the table given below:

There are 3 steps involved in Operation and Operator method:

• Step 1: We will multiply the unit place of the given number by the corresponding operator.

• Step 2: Thereafter we will apply the corresponding operation (subtraction or addition) on remaining part of the given number.

• Step 3: We will repeat these two steps till we can identify that the resultant difference is a multiple of the divisor or not. If this resultant difference is a multiple of divisor, then the given number is also a multiple of divisor, otherwise it is not.

Let’s understand all this using some examples.

Divisibility by 7

Find whether 2142 is a multiple of 7 or not.

For 7, the operator is 2 and operation is subtraction.

214 − (2 × 2) = 210
21 − (2 × 0) = 21
2 - (2 × 1) = 0

Hence 2142 is a multiple of 7.

Divisibility by 13

Find whether 2795 is a multiple of 13 or not.

For 13, the operator is 4 and operation is addition.

279 + (4 × 5) = 299
29 + (4 × 9) = 65
6 + (4 × 5) = 26
2 + (4 × 6) = 26

26 is divisible by 13. So, 2795 will also be divisible by 13.

Divisibility by 17

Find whether 3383 is a multiple of 17 or not.

For 17, the operator is 5 and operation is subtraction.

338 - (5 × 3) = 323
32 - (5 × 3) = 17

17 is divisible by 17. So, 3383 will also be divisible by 17.

Divisibility by 19

Find whether 1159 is a multiple of 19 or not.

For 19, the operator is 2 and operation is addition.

115 + (2 × 9) = 133
13 + (2 × 3) = 19

19 is divisible by 19. So, 1159 will also be divisible by 19.

Divisibility by 11

To check divisibility by 11, we will use Alternate Digital Sum method.

A number is divisible by 11, if the difference of the sum of its digits at odd places and the sum of its digits at even places, is either 0 or a number divisibly by 11.

Find whether 1144 is a multiple of 11 or not.
Sum of digits at odd places – Sum of digits at even places = (1 + 4) – (1 + 4) = 0
So, 1144 is divisible by 11.

Find whether 82346 is a multiple of 11 or not.
Sum of digits at odd places – Sum of digits at even places = (8 + 3 + 6) – (2 + 4) = 11.
As 11 is divisible by 11. So, 82346 too is divisible by 11.

Divisibility of polynomial expressions

Divisibility of $a^n – b^n$

$a^n – b^n$ is:

• always divisible by a – b.
  
  E.g. $5^3 – 2^3$ = 125 – 8 = 117, which is divisible by 5 – 2 = 3
  $5^2 – 2^2$ = 25 – 4 = 21, which is divisible by 5 – 2 = 3

• divisible by a + b, when n is even.
  
  E.g. $5^4 - 2^4$ = 625 – 16 = 609, which is divisible by 5 + 2 = 7

• divisible by a + b, when n is odd and a + b is a factor of 2$b^n$
  
  E.g. $5^3 - 2^3$ = 125 – 8 = 117, which is not divisible by 5 + 2 = 7. Because 7 is not a factor of 2$b^n$ = 2($2^3$)
  $6^3 - 2^3$ = 216 – 8 = 208, which is divisible by 6 + 2 = 8. Because 8 is a factor of 2$b^n$ = 2($2^3$) = 16

Divisibility of $a^n + b^n$

$a^n + b^n$ is:

• divisible by a + b, when n is odd.
  
  E.g. $5^3 + 2^3$ = 125 + 8 = 133, which is divisible by 5 + 2 = 7

• divisible by a – b, when n is odd and a - b is a factor of 2$b^n$
  
  E.g. $5^3 + 2^3$ = 125 + 8 = 133, which is not divisible by 5 – 2 = 3. Because 3 is not a factor of 2$b^n$ = 2($2^3$)
  $6^3 + 2^3$ = 216 + 8 = 224, which is divisible by 6 – 2 = 4. Because 4 is a factor of 2$b^n$ = 2($2^3$)

• divisible by a + b, when n is even and a + b is a factor of 2$b^n$
  
  E.g. $5^2 + 2^2$ = 25 + 4 = 29, which is not divisible by 5 + 2 = 7. Because 7 is not a factor of 2$b^n$ = 2($2^3$)
  $6^2 + 2^2$ = 36 + 4 = 40, which is divisible by 6 + 2 = 8. Because 8 is a factor of 2$b^n$ = 2($2^2$) = 8