Finding Time

In this article we will study how to find the time at which two hands make a particular angle with each other.

So, angle will be given and we will be supposed to find the time.

To do so we need to have a firm grasp on the Concept of Relative Speed.

Concept of Relative Speed

Motion in Straight line

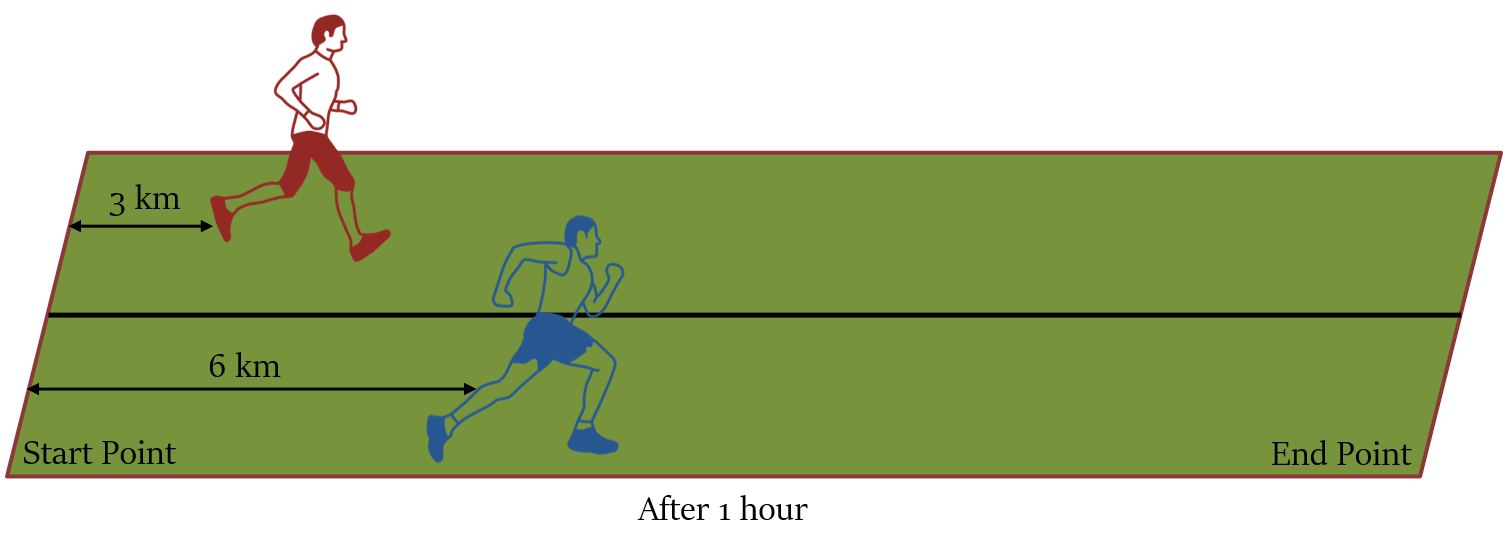
In the figure given below, two runners, Mr. Red and Mr. Blue, start from the same start point, with speeds of 3 km/hr and 6 km/hr, respectively, in the same direction towards the end point.

We can see that every hour the faster runner covers 3 km more distance than the distance traveled by the slower runner. Therefore, every hour the distance between the slower runner and the faster runner increases by 3 km.

So, the gap between the runners is:

• 3 km in one hour.

• 6 km in two hours.

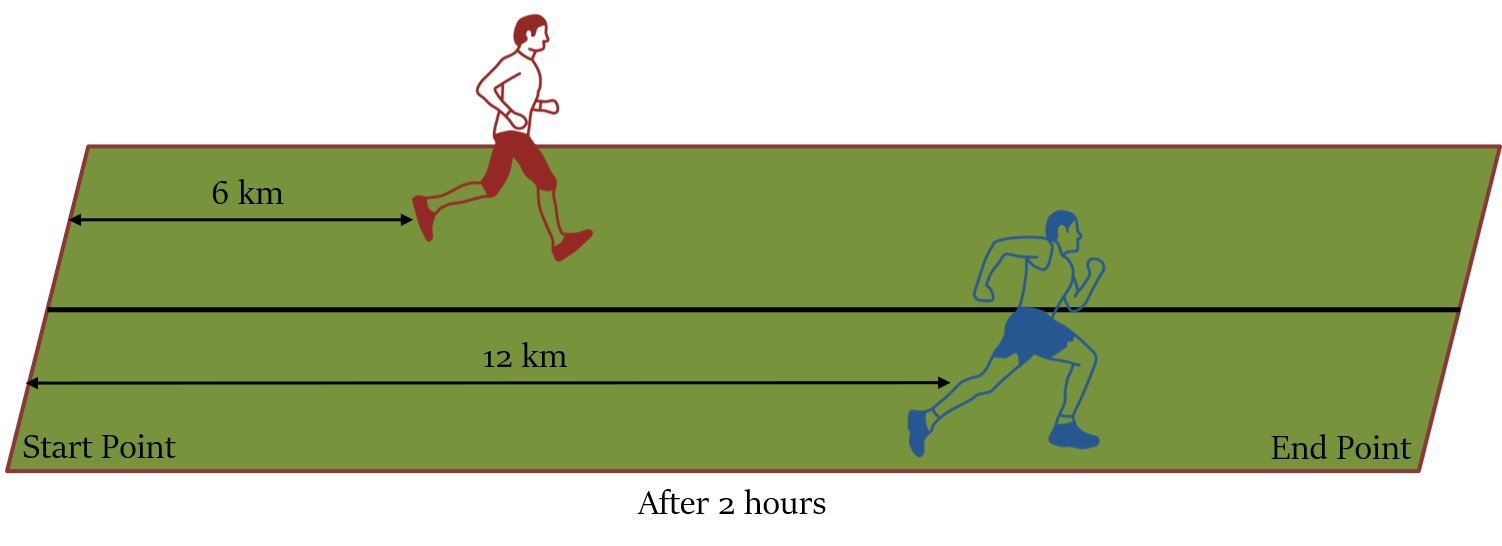
• 9 km in three hours, and so on.

Note that the gap between the runners does not depend on their absolute speeds but the difference between their speeds. The gap would still be increasing by 3 km every hour if the speeds of the runners were 5 km/hr and 2 km/hr.

Thus, relative speed is nothing but the distance reduced/increased between the two per unit time, which in this case is the difference in their speeds, i.e. 6 – 3 = 3 km/hr.

Relative Speed Formula

Basic TSD formula is: Distance = Speed × Time

Similarly, Relative speed formula is: Relative Distance = Relative Speed × Time

Circular Motion

Motion on a circular track is very similar to motion in straight line. We can use the same formula of relative speed here too. We will study circular motion in much more detail in time, speed & distance chapter. Here let us just focus on the part which we need know to solve questions based on clocks.

Suppose our two runners, Mr. Red and Mr. Blue start running on a circular track, in the same direction and from the same point, with speeds of 3 m/sec and 6 m/sec, respectively.

The moment Mr. Blue and Mr. Red start from the starting point, Mr. Blue starts getting ahead of Mr. Red. Every second, Mr. Blue increases the gap between Mr. Red and him by 3 m.

Therefore, the gap between Mr. Blue and Mr. Red is 3 m after 1 second, 6 m after 2 seconds, 9 m after 3 seconds, and so on. (similar to what was the case when they were running in a straight line)

You may realize that the two hands of a clock are nothing but two runners running around a circular track in the same direction.

• Both hands move in the same direction i.e., (clockwise direction).
• The minute hand moves around the whole circumference of the clock once in 1 hour. While, the hour hand moves around the whole circumference of the clock once in 12 hours. Thus, the minute hands is twelve times faster than the hour hand.

In angular terms:

The speed of the minute hand = $6^o$ per minute

And, speed of the hour hand = $0.5^o$ per minute.

Hence, the relative speed of the minute hand with respect to the hour hand = $6^o$ – $0.5^o$ = $5.5^o$ per minute.

In minute terms:

The distance between two consecutive numbers in the clock is equal to 5 min.

In an hour, the hour hand crosses 5 min spaces while the minute hand crosses 60 min spaces.

So, in 60 min, the minute hand gains (60 – 5) = 55 min over hour hand.

Hence, in 1 minute, the minute hand gains 55/60 = 11/12 minutes

Q. The two hands of a clock overlap at 12 o’clock. What will be the distance between hour and minute hands of the clock 10 minutes past 12 o’clock?

Explanation:

Finding Time

In some type of questions, we are asked to find out the time when the hands of the clock:

• overlap (i.e. $0^o$ angle between them).
• are opposite to each other (i.e. $180^o$ angle between them), or
• make some other angle between them.

Here again there are multiple methods that you can use. Let’s understand them via some examples.

Q. At what time between 3:00 pm and 4:00 pm, will the minute hand and the hour hand overlap?

(a) 16 $\frac{4}{11}$ minutes past 3 pm (b) 15 $\frac{4}{11}$ minutes past 3 pm
(c) 16 $\frac{2}{7}$ minutes past 3 pm (d) 15 $\frac{3}{5}$ minutes past 3 pm

Explanations :
1 2

Some more properties of clocks

1. In every hour, the two hands are in the same straight line two times:

• When both hands are coincident (i.e. in the same direction), i.e. angle between the two hands = 0°
  The two hands are 0 min apart.
  
  So, in every 12 hr both hands coincide 11 times.
  (between 11 and 1 O’clock there is a common position at 12 O’clock).
  
  And in 24 hrs, both hands coincide 22 times.

• When both hands are opposite to each other, i.e. angle between the two hands = 180°
  The two hands are 30 min spaces apart.
  
  In every 12 hr, both hands are in opposite direction 11 times.
  (between 5 and 7 O’clock there is a common position at 6 O’clock).
  
  In 24 hr, both hands are in opposite direction 22 times.
  

2. Hence, in every 12 hr, the two hands are in the same straight line 22 times.
   In 24 hr, the two hands are in the same straight line 44 times.

3. In every hour, both the hands are at right angles two times, i.e. angle between the two hands = 90°
   In other words, the two hands are 15 min spaces apart.
   
   In every 12 hr, the two hands are at right angles 22 times.
   (between 2 and 4 O’clock there is a common position at 3 O’clock and also between 8 and 10 O’clock there is a common position at 9 O’clock).
   
   Hence, in 24 hr, both the hands are at right angles 44 times.
   

Concept of Successive Meets

Let us again consider our example of two runners.

Suppose our two runners, Mr. Red and Mr. Blue start running on a circular track, in the same direction and from the same point, with speeds of 3 m/s and 6 m/s, respectively.

The moment Mr. Blue and Mr. Red start from the starting point, Mr. Blue starts getting ahead of Mr. Red. If they keep on running then a time will come when Mr. Blue will overtake Mr. Red again. The extra distance that Mr. Blue covered will be equal to the circumference of the circle.

If circumference of the circle is 600 m, then time taken by Mr. Blue to catch up with Mr. Red again = $\frac{Circumference \hspace{1ex} of \hspace{1ex} the \hspace{1ex} circle}{Relative \hspace{1ex} speed}$
= $\frac{600}{(6 - 3)}$ = $\frac{600}{3}$ = 200 s.

Let’s see an example.

Q. What is the time interval between two successive meets of the minute hand and the hour hand?

(a) 64 $\frac{5}{11}$ minutes (b) 65 $\frac{5}{11}$ minutes
(c) 66 $\frac{3}{11}$ minutes (d) 65 $\frac{4}{9}$ minutes

Explanations :
1 2 3