List of Trigonometric Formulae
In this article, we are going to list down all the important Trigonometric Formulas. Try to remember these.
For the purpose of objective-type aptitude examinations, we need not know how to drive them. But we should remember them, and develop our capability to use the right formula when required.
Relation among Trigonometric identities
When angles are same
Type 1
sin θ × cosec θ = 1
cos θ × sec θ = 1
tan θ × cot θ = 1
For example, sin θ × cosec Φ ≠ 1
Type 2
$sin^2$ θ + $cos^2$ θ = 1
$sec^2$ θ - $tan^2$ θ = 1
$cosec^2$ θ - $cot^2$ θ = 1
For example, $sin^2$ θ + $cos^2$ Φ ≠ 1
Type 3
If sin θ + cosec θ = 2, then:
$sin^n θ + cosec^n θ$ = 2 (where n is a natural number)
If cos θ + sec θ = 2, then:
$cos^n θ + sec^n θ$ = 2 (where n is a natural number)
If tan θ + cot θ = 2, then:
$tan^n θ + cot^n θ$ = 2 (where n is a natural number)
Type 4
If:
I. a sin θ + b cos θ = c and
II. b sin θ – a cos θ = d or a cos θ - b sin θ = d
Then, $c^2 + d^2$ = $a^2 + b^2$
If:
I. sin θ + cos θ = c and
II. sin θ – cos θ = d
Then, $c^2 + d^2$ = 2
If:
I. a sec θ + b tan θ = c; b sec θ + a tan θ = d, or
II. a sec θ - b tan θ = c; b sec θ - a tan θ = d
Then, $a^2 - b^2$ = $c^2 - d^2$
If:
I. a cosec θ + b cot θ = c; b cosec θ + a cot θ = d, or
II. a cosec θ - b cot θ = c; b cosec θ - a cot θ = d
Then, $a^2 - b^2$ = $c^2 - d^2$
When sum of angles is 90°
If θ + ɸ = 90°, then:
sin θ × sec ɸ = 1
or, sin θ = cos ɸ
cos θ × cosec ɸ = 1
or, cos θ = sin ɸ
tan θ × tan ɸ = 1
or, tan θ = cot ɸ
cot θ × cot ɸ = 1
or, cot θ = tan ɸ
If θ + ɸ + α = 90°, then:
(tan θ × tan ɸ) + (tan ɸ × tan α) + (tan α × tan θ) = 1
cot θ + cot ɸ + cot α = cot θ × cot ɸ × cot α
When sum of angles is 180°
If θ + ɸ = 180°, then:
sin θ × cosec ɸ = 1
If θ + ɸ + α = 180° (i.e. we are talking about a triangle), then:
tan θ + tan ɸ + tan α = tan θ × tan ɸ × tan α
(cot θ × cot ɸ) + (cot ɸ × cot α) + (cot θ × cot α) = 1
When sum of angles is 45° or 225°
If θ + ɸ = 45° or 225°, then:
(1 + tan θ) (1 + tan ɸ) = 2
(cot θ - 1) (cot ɸ - 1) = 2, Or
(1 - cot θ) (1 - cot ɸ) = 2
When difference of angles is 45° or 225°
If θ - ɸ = 45° or 225°, then:
(1 + tan θ) (1 - tan ɸ) = 2
(1 - cot θ) (1 + cot ɸ) = 2
Sum and Difference formulae
Type 1
sin (A ± B) = sin A . cos B ± cos A . sin B
cos (A ± B) = cos A . cos B ∓ sin A . sin B
tan (A ± B) = $\frac{tan A \hspace{1ex} ± \hspace{1ex} tan B}{1 \hspace{1ex} ∓ \hspace{1ex} tan A \hspace{1ex} . \hspace{1ex} tan B}$
cot (A ± B) = $\frac{cot A \hspace{1ex} . \hspace{1ex} cotB \hspace{1ex} ∓ \hspace{1ex} 1}{cot A \hspace{1ex} ± \hspace{1ex} cot B}$
Type 2
sin (A + B) + sin (A - B) = 2 sin A . cos B
sin (A + B) - sin (A - B) = 2 cos A . sin B
cos (A + B) + cos (A - B) = 2 cos A . cos B
cos (A - B) - cos (A + B) = 2 sin A . sin B
Type 3
sin 2A – sin 2B = sin (A + B) . sin (A - B)
cos 2A - cos 2B = cos (A + B) . cos (A - B)
Type 4
sin A + sin B = 2 sin [$\frac{A + B}{2}$] . cos [$\frac{A - B}{2}$]
sin A – sin B = 2 cos [$\frac{A + B}{2}$] . sin [$\frac{A - B}{2}$]
cos A + cos B = 2 cos [$\frac{A + B}{2}$] . cos [$\frac{A - B}{2}$]
cos A – cos B = 2 sin [$\frac{A + B}{2}$] . sin [$\frac{B - A}{2}$]
Trigonometric ratios of Angle Multiples
sin
sin (2θ) = 2 sin θ cos θ = $\frac{2 \hspace{1ex} tan θ}{1 + tan^2θ}$
sin (3θ) = $3 \hspace{1ex} sin θ - 4 \hspace{1ex} sin^3 θ = sin θ (- 1 + 4 \hspace{1ex} cos^2 θ)$
sin (4θ) = $cos θ (4 \hspace{1ex} sin θ - 8 \hspace{1ex} sin^3 θ) = sin θ (- 4 \hspace{1ex} cos θ + 8 \hspace{1ex} cos^3 θ)$
sin (5θ) = $5 \hspace{1ex} sin θ - 20 \hspace{1ex} sin^3 θ + 16 \hspace{1ex} sin^5 θ = sin θ (1 - 12 \hspace{1ex} cos^2 θ + 16 \hspace{1ex} cos^4 θ)$
cos
cos (2θ) = $cos^2 θ - sin^2 θ = 2 \hspace{1ex} cos^2 θ - 1 = 1 - 2 \hspace{1ex} sin² θ = \frac{1 - tan² θ}{1 + tan² θ}$
cos (3θ) = $cos^3 θ - 3 \hspace{1ex} cos θ sin^2 θ = 4 \hspace{1ex} cos^3 θ - 3 \hspace{1ex} cos θ$
cos (4θ) = $cos^4 θ - 6 \hspace{1ex} cos^2 θ sin^2 θ + sin^4 θ = 1 - 8 \hspace{1ex} cos^2 θ + 8 \hspace{1ex} cos^4 θ$
cos (5θ) = $cos^5 θ - 10 \hspace{1ex} cos^3 θ sin^2 θ + 5 \hspace{1ex} cos θ sin^4 θ = 5 \hspace{1ex} cos θ - 20 \hspace{1ex} cos^3 θ + 16 \hspace{1ex} cos^5 θ$
tan
tan (2θ) = $\frac{2 \hspace{1ex} tan θ}{1 - tan^2 θ}$
tan (3θ) = $\frac{3 \hspace{1ex} tan θ - tan^3 θ}{1 - 3 \hspace{1ex} tan^2 θ}$
tan (4θ) = $\frac{4 \hspace{1ex} tan θ - 4 \hspace{1ex} tan^3 θ}{1 - 6 \hspace{1ex} tan^2 θ + tan^4 θ}$
Morri’s law
sin θ . sin(60° - θ) . sin (60° + θ) = $\frac{1}{4}$ sin 3θ
cos θ . cos(60° - θ) . cos (60° + θ) = $\frac{1}{4}$ cos 3θ
tan θ . tan (60° - θ) . tan (60° + θ) = tan 3θ
cot θ . cot (60° - θ) . cot (60° + θ) = cot 3θ
Maximum/Minimum Values
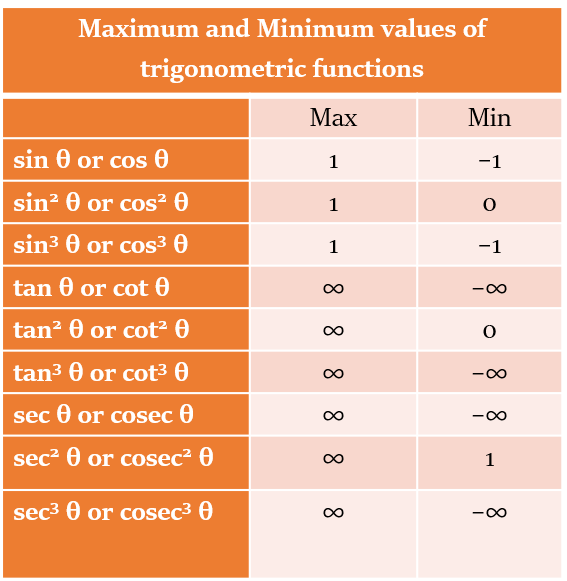
The value of sec & cosec can be anything between -∞ to ∞. However, it can’t be between -1 and 1 (thouggh it can be -1 and 1).
That is, the range of value of sec & cosec = ∞ - (-1, 1)
Maximum value of $sin^n θ \hspace{1ex} cos^n θ = (1/2)^n$
Minimum value of $sin^n θ \hspace{1ex} cos^n θ = -(1/2)^n$ or 0 (if n is even)
Maximum value of $sin^n θ + cos^n θ = 1$ (always)
Minimum value of $sin^n θ + cos^n θ$ will be when θ = 45°
Maximum value of a sin θ ± b cos θ = $√(a^2 + b^2)$
Minimum value of a sin θ ± b cos θ = – $√(a^2 + b^2)$Maximum value of $a \hspace{1ex} sin^2 θ + b \hspace{1ex} cos^2 θ$ = a (If a>b) or b (If b>a)
Minimum value of $a \hspace{1ex} sin^2 θ + b \hspace{1ex} cos^2 θ$ = b (If a>b) or a (If b>a)
Minimum value of $a \hspace{1ex} sin^2 θ + b \hspace{1ex} cosec^2 θ = 2√ab$ when b ≤ a, Or a + b, when b ≥ a
Minimum value of $a \hspace{1ex} cos^2 θ + b \hspace{1ex} sec^2 θ = 2√ab$ when b ≤ a, Or a + b, when b ≥ a
Minimum value of $a \hspace{1ex} tan^2 θ + b \hspace{1ex} cot^2 θ = 2√ab$
Minimum value of $a \hspace{1ex} sec^2 θ + b \hspace{1ex} cosec^2 θ = (√a + √b)^2$