Basics of Quadratic Equations
What is a Quadratic Equation?
They are equations of second degree. For example,
Depending on the number of variables in a quadratic equation, we can further divide them into the following types:
- Quadratic equations in one variable - e.g.
- Quadratic equations in two variables - e.g.
- Quadratic equations in three variables and so on.
Quadratic equations in one variable
Equations of the form
For example,
The numbers a, b and c are called the coefficients of this equation.
Graph of Quadratic equation in one variable
Graph of a quadratic equation in one variable is a parabola.
For example, the quadratic equation 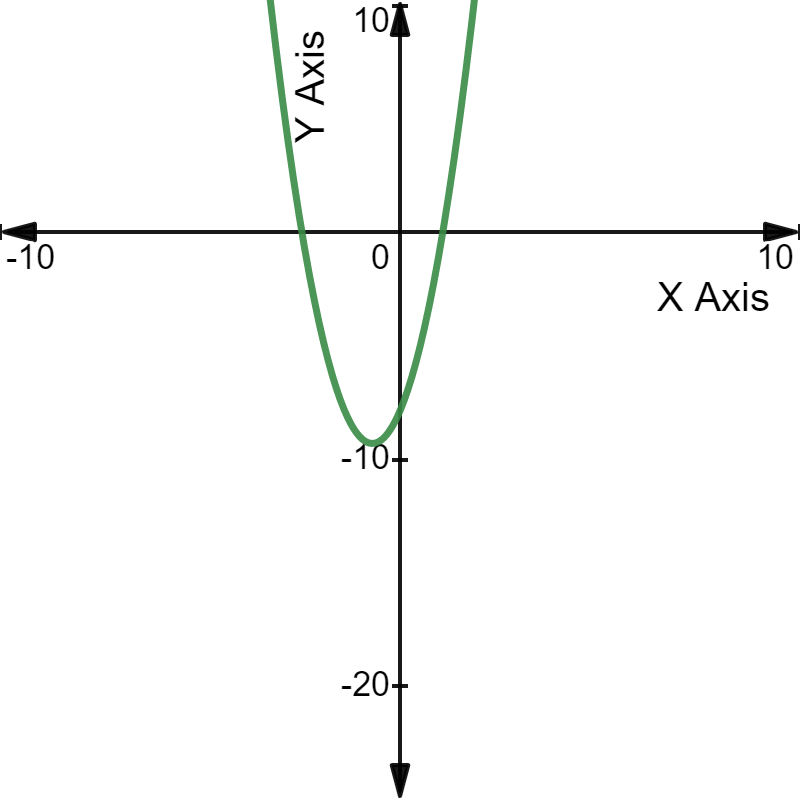
The quadratic equation 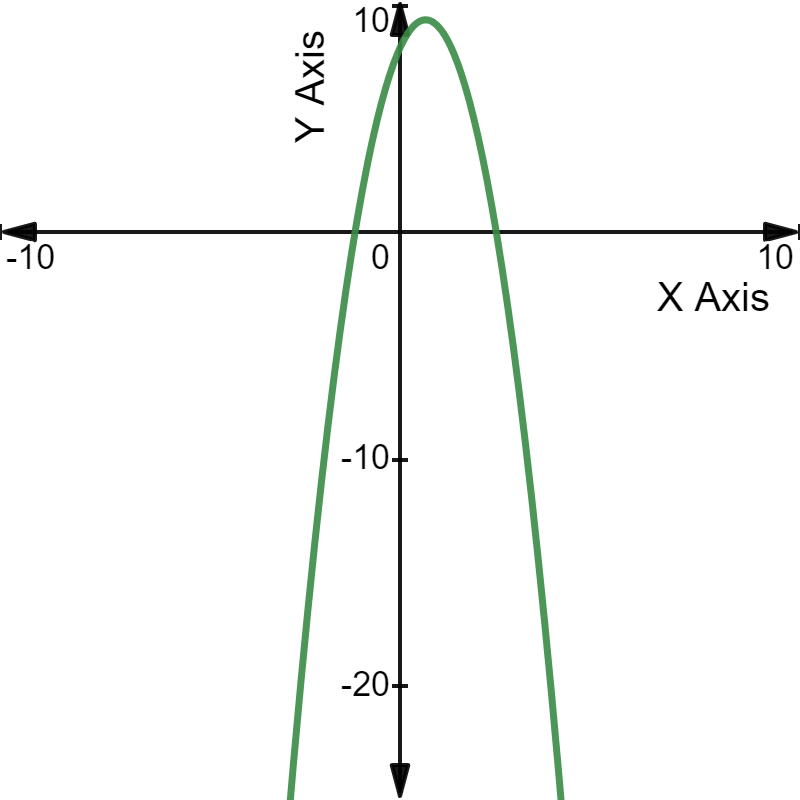
The quadratic equation 
The quadratic equation 
Roots of Quadratic equations in one variable
Root(s) of a quadratic equation in one variable are the values of the variable, at which the value of the quadratic expression becomes zero.
Roots of a quadratic equation
x =
The expression
The value of D decides whether a quadratic equation has one or two roots, and whether they are real or imaginary.
D > 0
If D > 0, then
In graphical terms, we can say that the parabola of that quadratic equation will intersect the X-axis at two places.
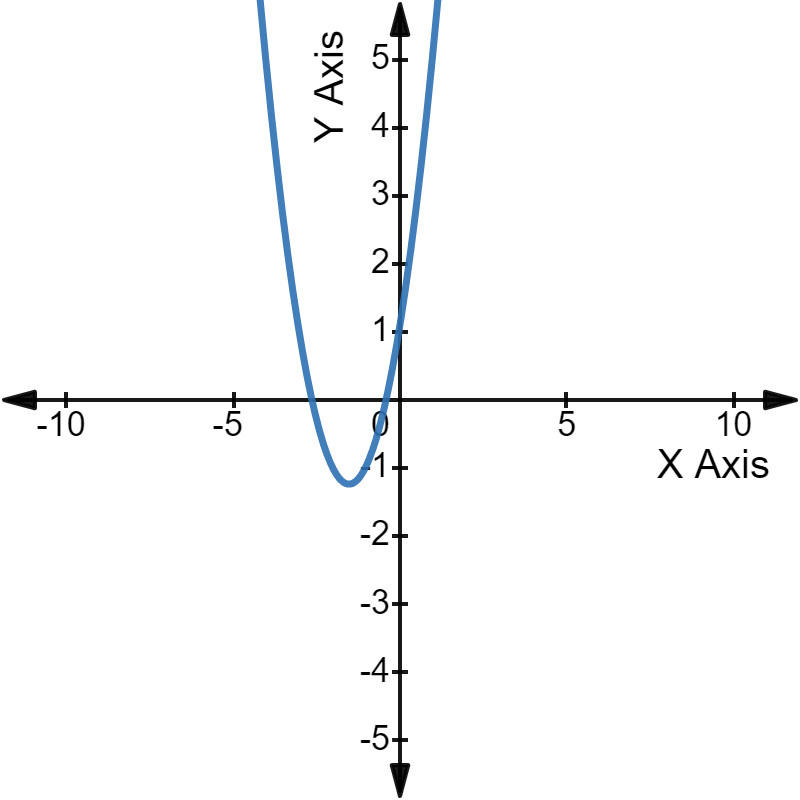
Here, the x-intercepts of the parabola are the solutions/roots of the quadratic equation.
D = 0
If D = 0, then
In graphical terms, we can say that the parabola of that quadratic equation will touch the X-axis at one place only.
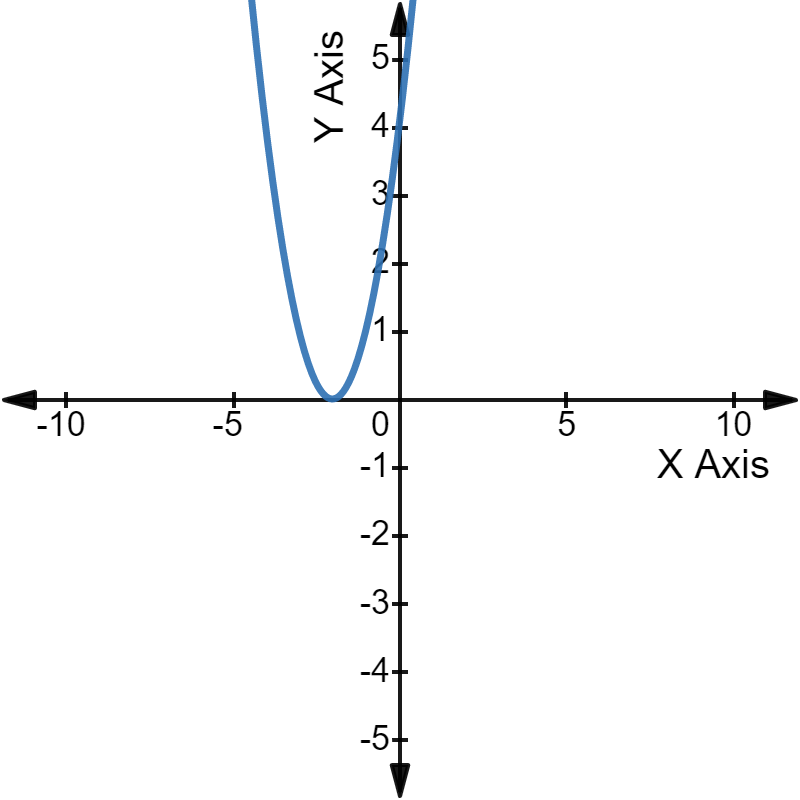
Here, the x-intercept of the parabola is the solution/root of the quadratic equation.
D < 0
If D < 0, then
In graphical terms, we can say that the parabola of that quadratic equation will not touch or intersect the X-axis at all.
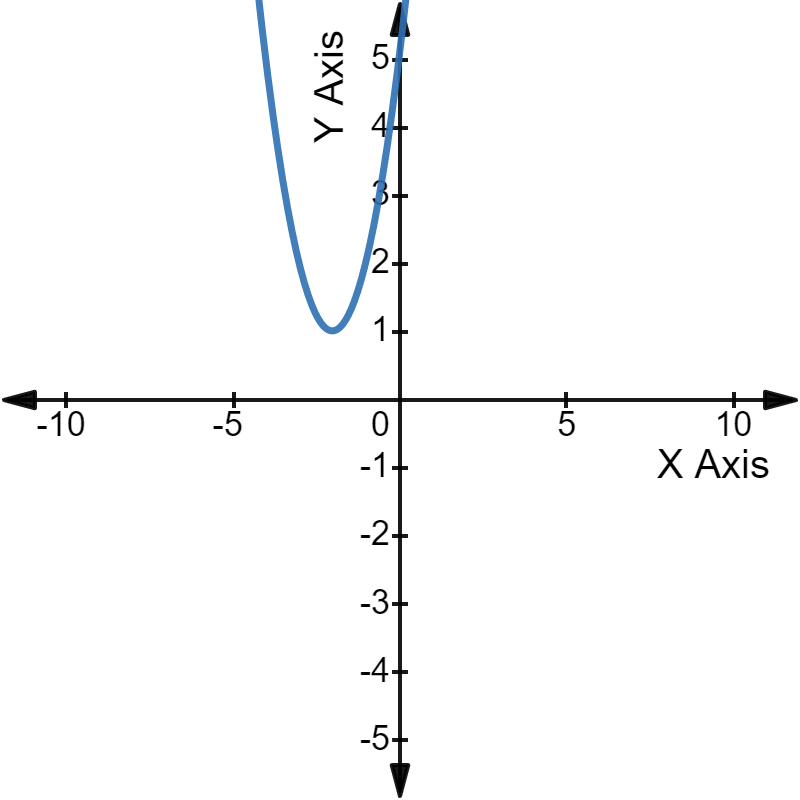
As the parabola has not even touched the X-axis, there are no real roots of the corresponding quadratic equation.
Properties of Quadratic equations
Property 1
A quadratic equation in one variable can have 0, 1 or 2 real roots. It cannot have more than two different roots.
Property 2
If m is a root of the quadratic equation a
Property 3: Sum of Roots
If α and β are the roots of the quadratic equation a
Sum of Roots, α + β = -
Property 4: Product of Roots
If α and β are the roots of the quadratic equation a
Product of Roots, α × β =
If α, β, and γ are the roots of the cubic equation a
Sum of Roots, α + β + γ = -
αβ + βγ + γα =
Product of Roots, α × β × γ = -
Just as a quadratic equation may have two real roots, a cubic equation may have three. But unlike a quadratic equation which may have no real root, a cubic equation always has at least one real root.
Signs of the Roots
Now, let us understand how to find the signs of the roots of a quadratic equation, using the signs of the coefficients. This is called the Sign Method. It can be pretty handy in objective type questions.
We will consider the quadratic equation a
Now, four cases are possible when it comes to the signs of b and c.
Case 1: b+, c+
If both b and c are positive, then both the roots will be negative.
For example, have a look at the graph of the quadratic equation 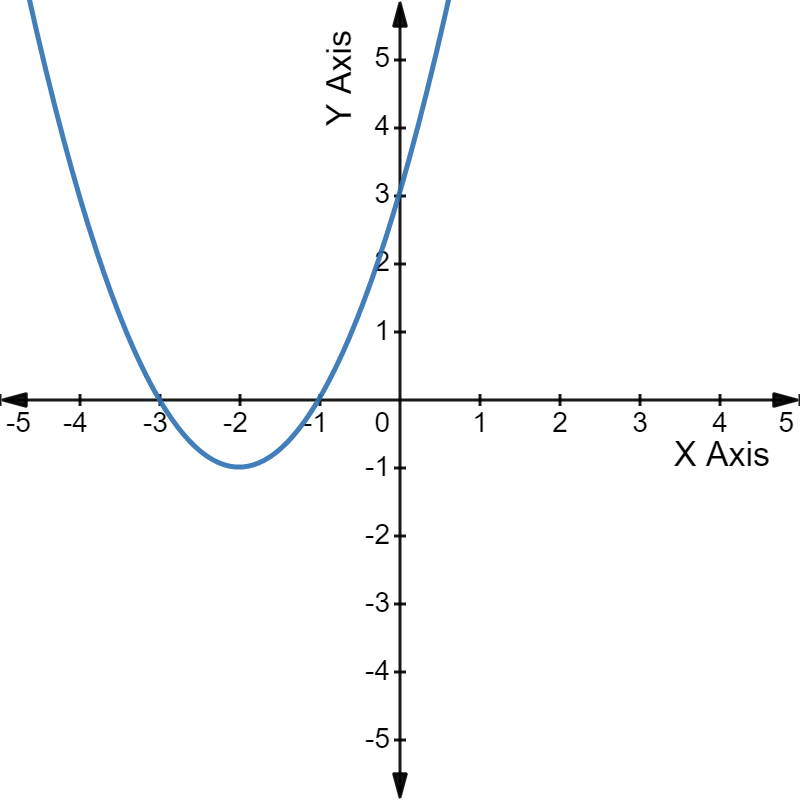 The parabola intercepts the X-axis at -1 and -3, the two roots of the given equation.
The parabola intercepts the X-axis at -1 and -3, the two roots of the given equation.
Case 2: b-, c-
If both b and c are negative, then:
- one root will be positive (the bigger number)
- one root will be negative (the smaller number)
For example, have a look at the graph of the quadratic equation 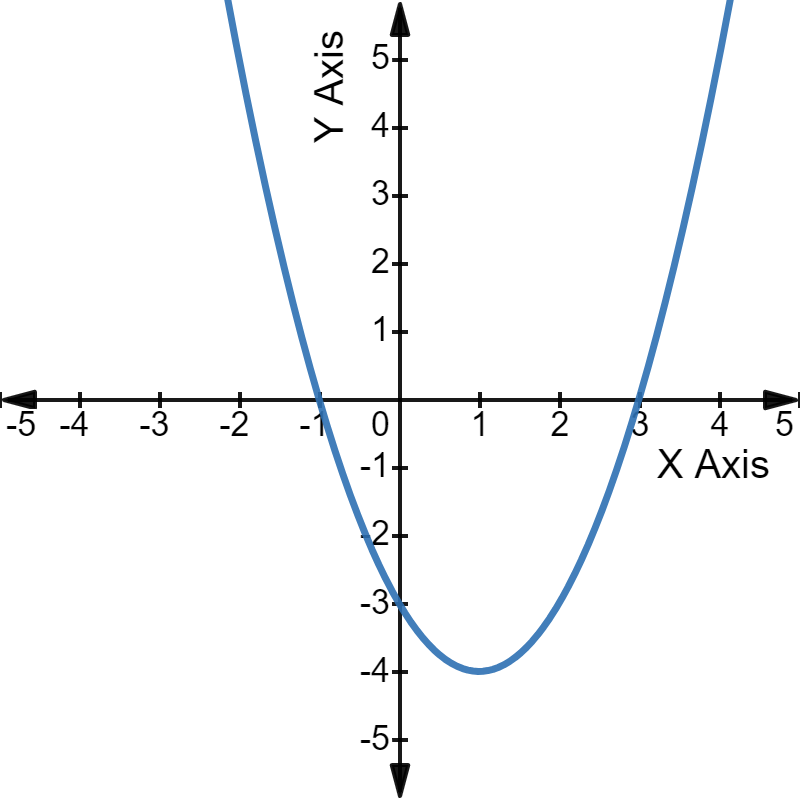 The parabola intercepts the X-axis at -1 and 3, the two roots of the given equation.
The parabola intercepts the X-axis at -1 and 3, the two roots of the given equation.
Case 3: b+, c-
If b is positive and c is negative, then:
- one root will be positive (the smaller number)
- one root will be negative (the bigger number)
For example, have a look at the graph of the quadratic equation 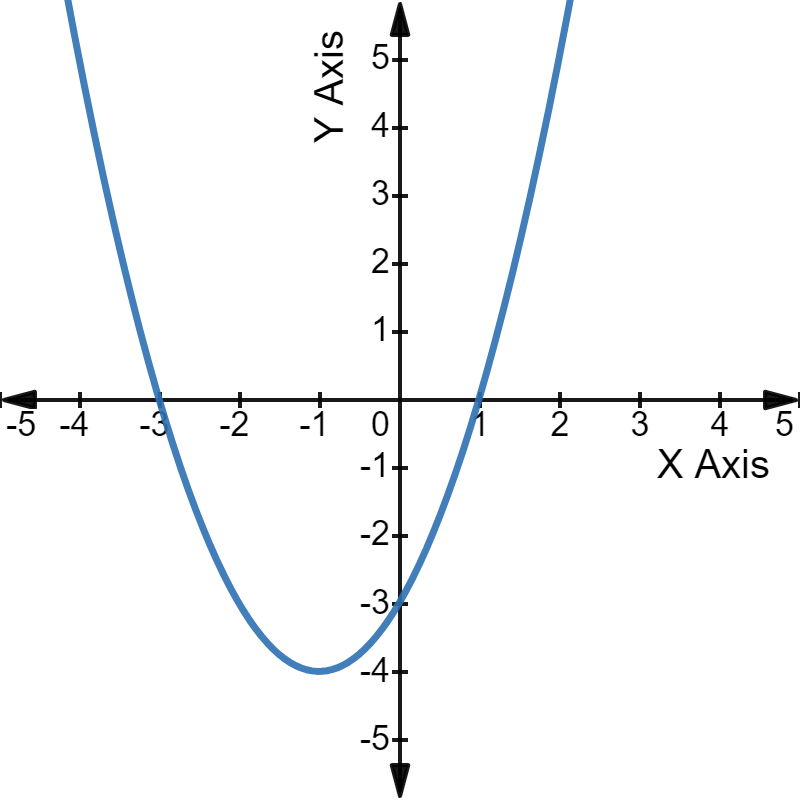 The parabola intercepts the X-axis at 1 and -3, the two roots of the given equation.
The parabola intercepts the X-axis at 1 and -3, the two roots of the given equation.
Case 4: b-, c+
If b is negative and c is positive, then both the roots will be positive.
For example, have a look at the graph of the quadratic equation 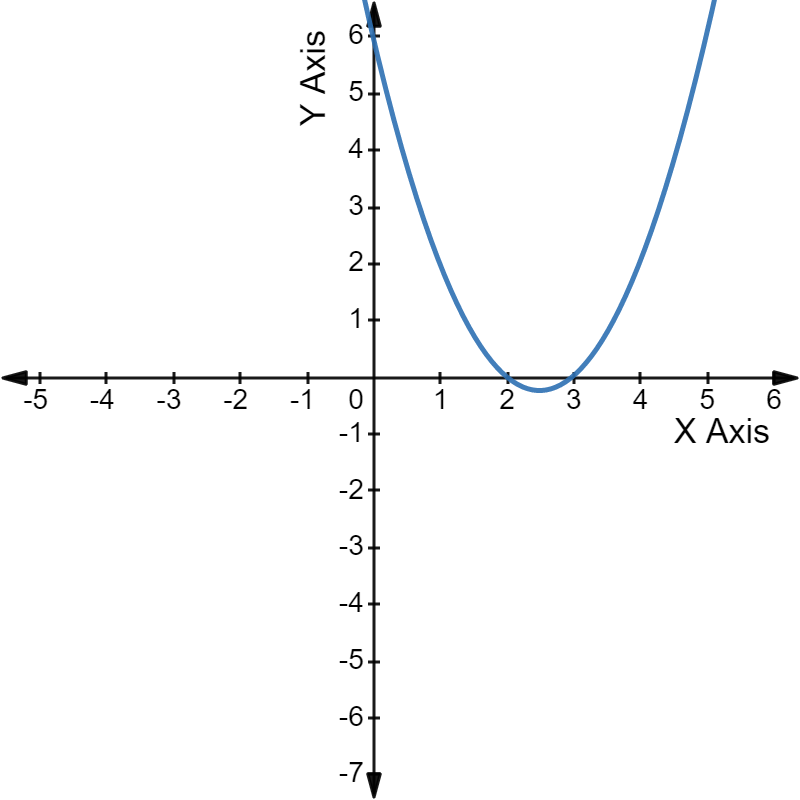 The parabola intercepts the X-axis at 2 and 3, the two roots of the given equation.
The parabola intercepts the X-axis at 2 and 3, the two roots of the given equation.
To summarize:
| Co-efficient of x (b) | Constant (c) | Root α | Root β |
|---|---|---|---|
| Positive | Positive | - | - |
| Negative | Negative | + (bigger number) | - (smaller number) |
| Positive | Negative | + (smaller number) | - (bigger number) |
| Negative | Positive | + | + |
How to find the Roots of a Quadratic Equation?
To find the roots of a quadratic equation, write it in the form a
Now two cases may arise.
Case 1: a = 1
If the coefficient of
Step 1: Find two numbers, m and n, such that the product of these two is equal to c and their sum is equal to b. (While doing so, we will consider the signs too)
Step 2: Now, we can rewrite the equation as: (x + m) (x + n) = 0. So, our roots are -m and -n.
Case 2: a > 1
In such a case, follow the following steps:
Step 1: Multiply the constant term c with a. Now, find two numbers, m and n, such that the product of these two is equal to (c × a) and their sum is equal to b. (While doing so, we will consider the signs too)
Step 2: Now, we can rewrite the equation as: (x + m/a) (x + n/a) = 0. So, our roots are -m/a and -n/a.
Let us see some examples to make this concept clearer.
Q. Find the roots of the equation
Explanations :
Given equation:
So, a = 1; b = 4 and c = 3
As both b and c are positive, both of the roots of this equation must be negative.
Step 1: We will find two numbers, such that their product is equal to c (i.e. 3) and their sum is equal to b (i.e. 4).
We can see that: 1 × 3 = 3, and 1 + 3 = 4Step 2: So, we can rewrite the given equation as: (x + 1)(x + 3) = 0.
So, our roots will be -1 and -3.
 The parabola intercepts the X-axis at -1 and -3, the two roots of the given equation.
The parabola intercepts the X-axis at -1 and -3, the two roots of the given equation.Q. Find the roots of the equation 2
Explanations :
Given equation: 2
So, a = 2; b = -17 and c = 30
As b is negative, and c is positive, both of the roots of this equation must be positive.
Step 1: We will find two numbers, such that their product is equal to c × a (i.e. 30 × 2 = 60) and their sum is equal to b (i.e. -17).
We can see that: (-5) × (-12) = 60, and (-5) + (-12) = -17Step 2: So, we can rewrite the given equation as: (x - 5/2)(x - 12/2) = 0, or (x - 2.5)(x - 6) = 0
So, our roots will be 2.5 and 6.
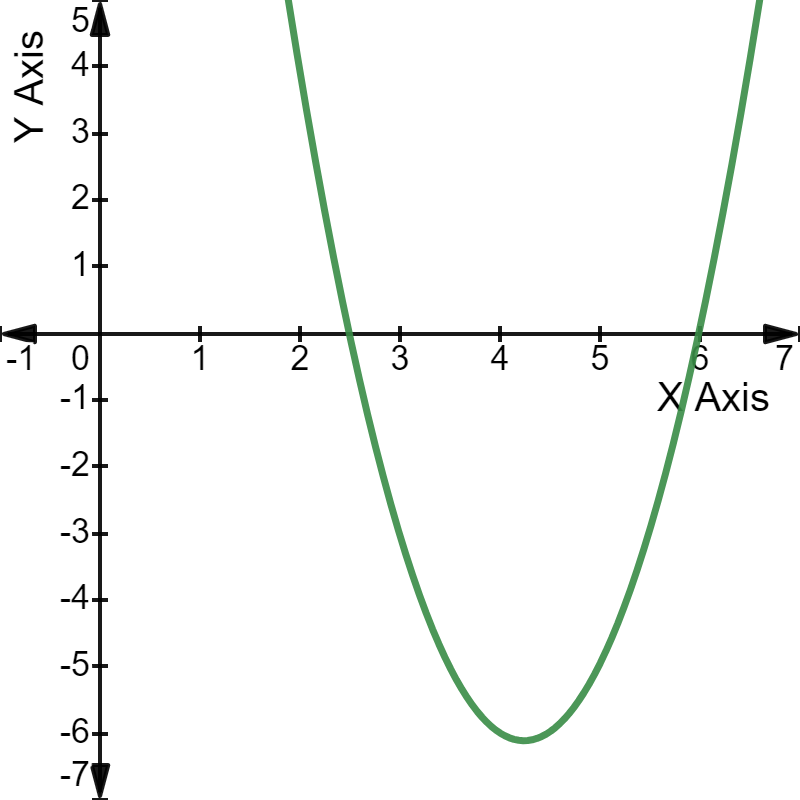 The parabola intercepts the X-axis at 2.5 and 6, the two roots of the given equation.
The parabola intercepts the X-axis at 2.5 and 6, the two roots of the given equation.