Basics of Quadratic Equations
What is a Quadratic Equation?
They are equations of second degree. For example, $x^2$ + x - 2 = 0, $x^2$ - 3y + 2 = 0
Depending on the number of variables in a quadratic equation, we can further divide them into the following types:
- Quadratic equations in one variable - e.g. $x^2$ + x + 1 = 0
- Quadratic equations in two variables - e.g. $y^2$ + x - 22 = 0
- Quadratic equations in three variables and so on.
Quadratic equations in one variable
Equations of the form $ax^2$ + bx + c = 0 are called quadratic equations in one variable. Here, a, b, c are real numbers and a ≠ 0.
For example, $3x^2$ + 4x - 32 = 0.
The numbers a, b and c are called the coefficients of this equation.
Graph of Quadratic equation in one variable
Graph of a quadratic equation in one variable is a parabola.
For example, the quadratic equation $3x^2$ + 4x - 8 = 0 can be plotted on a graph as follows:
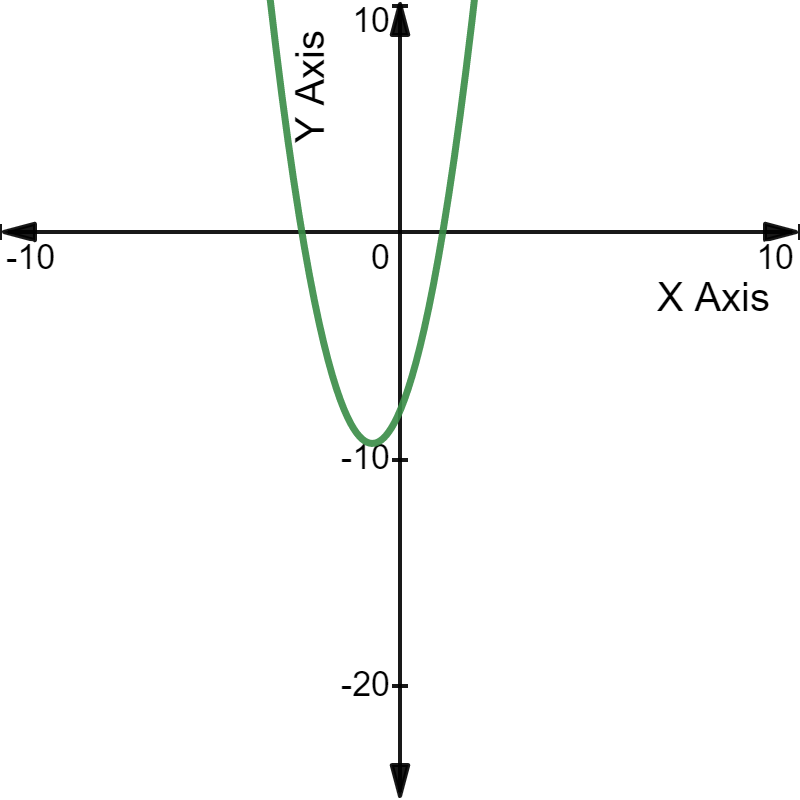
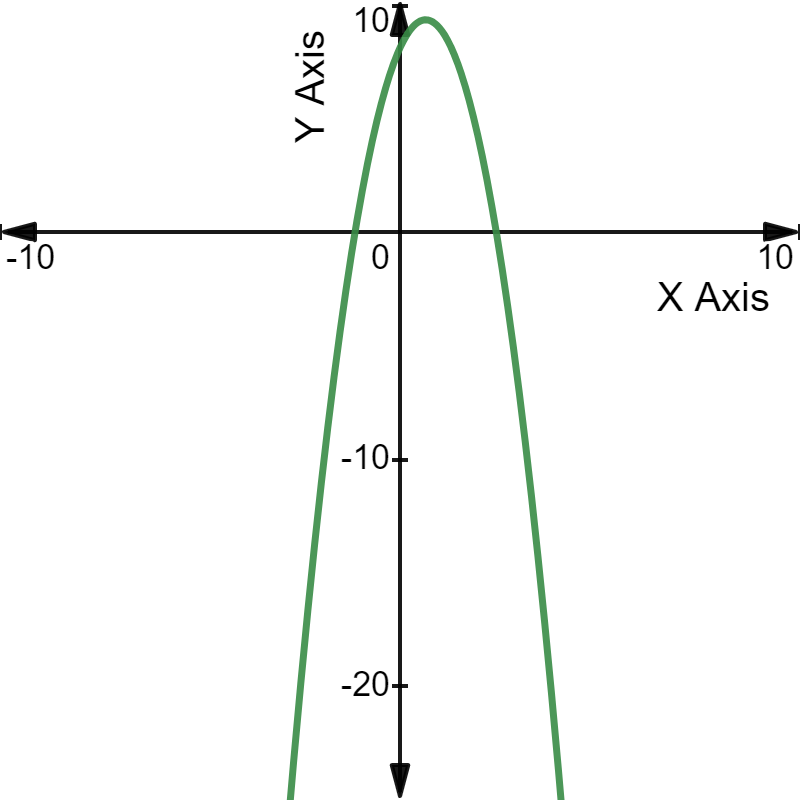
The quadratic equation $-3x^2$ + 4x + 8 = 0 can be plotted on a graph as follows:
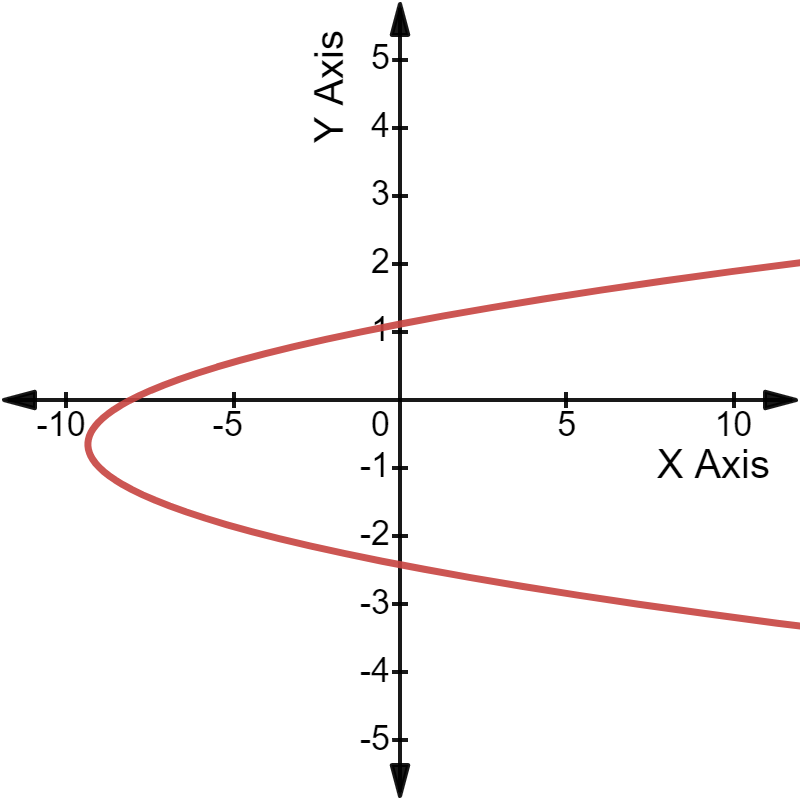
The quadratic equation $3y^2$ + 4y - 8 = 0 can be plotted on a graph as follows:
The quadratic equation $-3y^2$ + 4y + 8 = 0 can be plotted on a graph as follows:
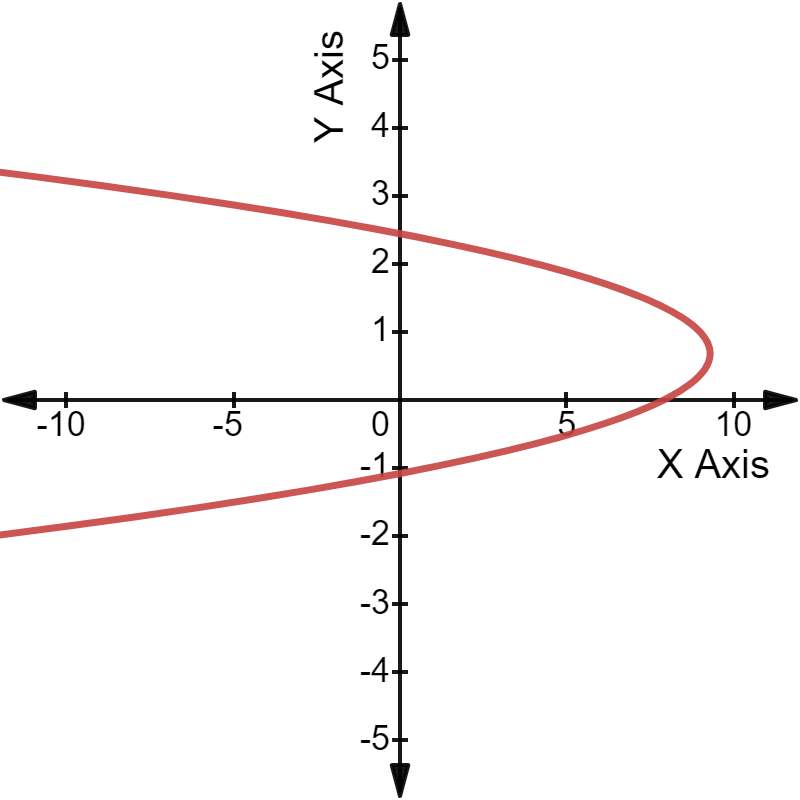
Roots of Quadratic equations in one variable
Root(s) of a quadratic equation in one variable are the values of the variable, at which the value of the quadratic expression becomes zero.
Roots of a quadratic equation $ax^2$ + bx + c = 0, i.e. the possible values of x, can be found using the following formula:
x = $\frac{-b ± \sqrt{b^2 - 4ac}}{2a}$
The expression $b^2 - 4ac$ is called the discriminant of this quadratic equation, and is denoted by D.
The value of D decides whether a quadratic equation has one or two roots, and whether they are real or imaginary.
D > 0
If D > 0, then $\sqrt{b^2 - 4ac}$ would have two real values, one positive and the other negative. So, the quadratic equation will have two distinct real roots.
In graphical terms, we can say that the parabola of that quadratic equation will intersect the X-axis at two places.
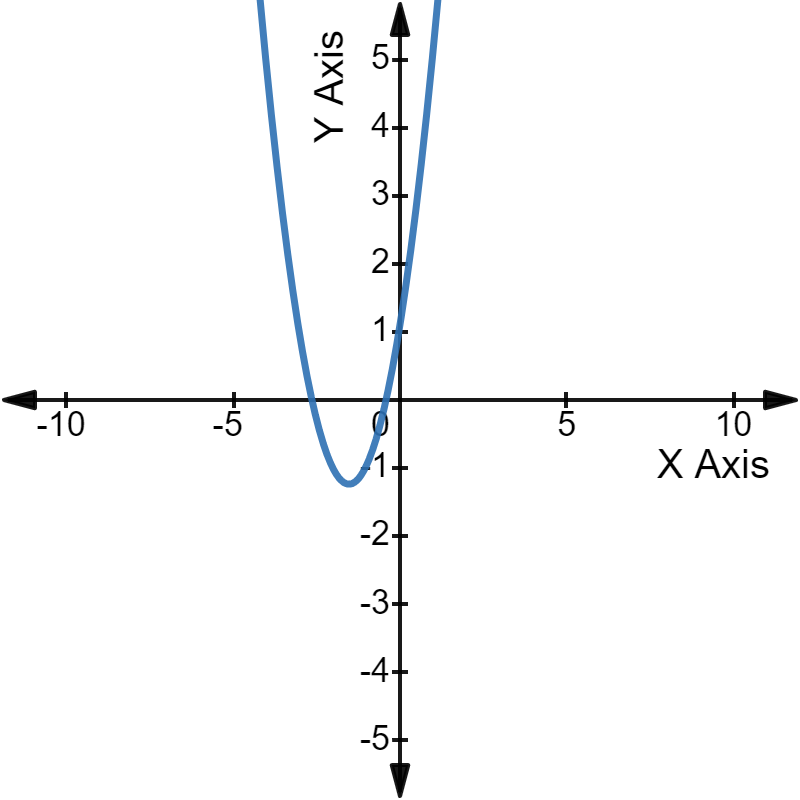
Here, the x-intercepts of the parabola are the solutions/roots of the quadratic equation.
D = 0
If D = 0, then $\sqrt{b^2 - 4ac}$ would have one real value, i.e. 0. So, the quadratic equation will have only one real root.
In graphical terms, we can say that the parabola of that quadratic equation will touch the X-axis at one place only.
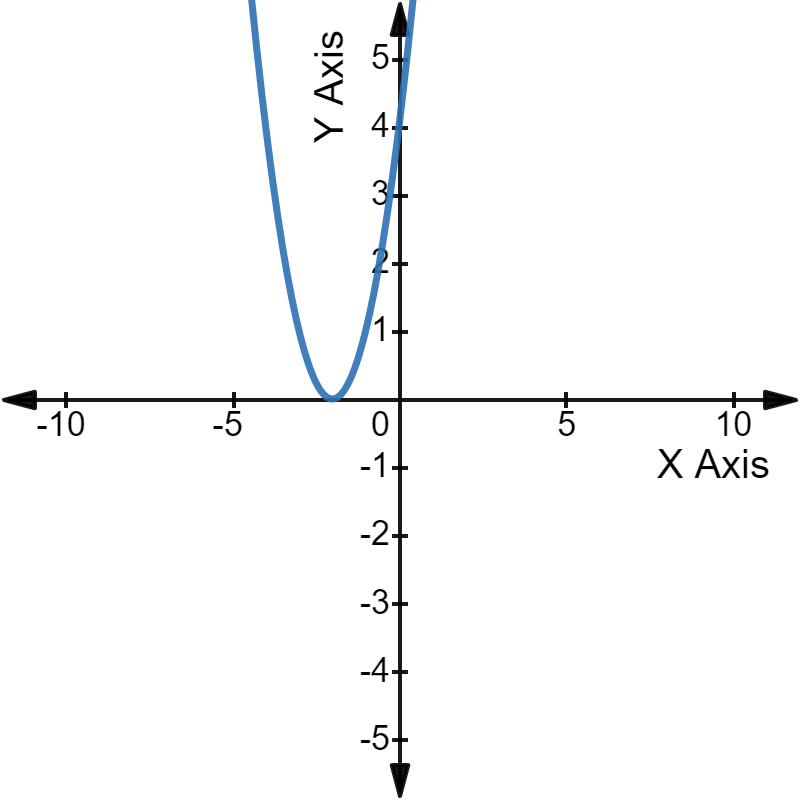
Here, the x-intercept of the parabola is the solution/root of the quadratic equation.
D < 0
If D < 0, then $\sqrt{b^2 - 4ac}$ would have no real value. So, the quadratic equation will have no real roots.
In graphical terms, we can say that the parabola of that quadratic equation will not touch or intersect the X-axis at all.
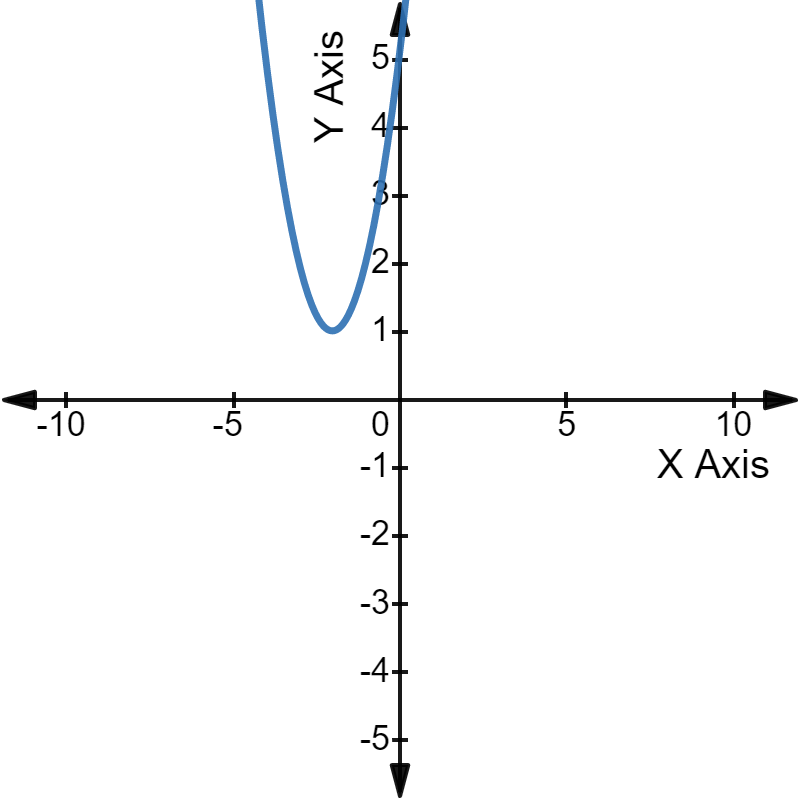
As the parabola has not even touched the X-axis, there are no real roots of the corresponding quadratic equation.
Properties of Quadratic equations
Property 1
A quadratic equation in one variable can have 0, 1 or 2 real roots. It cannot have more than two different roots.
Property 2
If m is a root of the quadratic equation a$x^2$ + bx + c = 0, then (x - m) must be a factor of that quadratic equation.
Property 3: Sum of Roots
If α and β are the roots of the quadratic equation a$x^2$ + bx + c = 0 (where a ≠ 0), then:
Sum of Roots, α + β = -$(\frac{Coefficient \hspace{1ex} of \hspace{1ex} x}{Coefficient \hspace{1ex} of \hspace{1ex} x^2})$ = -$(\frac{b}{a})$
Property 4: Product of Roots
If α and β are the roots of the quadratic equation a$x^2$ + bx + c = 0 (where a ≠ 0), then:
Product of Roots, α × β = $(\frac{Constant \hspace{1ex} Term}{Coefficient \hspace{1ex} of \hspace{1ex} x^2})$ = $(\frac{c}{a})$
If α, β, and γ are the roots of the cubic equation a$x^3$ + b$x^2$ + cx + d = 0 (where a ≠ 0), then:
Sum of Roots, α + β + γ = -$(\frac{Coefficient \hspace{1ex} of \hspace{1ex} x^2}{Coefficient \hspace{1ex} of \hspace{1ex} x^3})$ = -$(\frac{b}{a})$
αβ + βγ + γα = $(\frac{Coefficient \hspace{1ex} of \hspace{1ex} x}{Coefficient \hspace{1ex} of \hspace{1ex} x^3})$ = $(\frac{c}{a})$
Product of Roots, α × β × γ = -$(\frac{Constant \hspace{1ex} Term}{Coefficient \hspace{1ex} of \hspace{1ex} x^3})$ = -$(\frac{d}{a})$
Just as a quadratic equation may have two real roots, a cubic equation may have three. But unlike a quadratic equation which may have no real root, a cubic equation always has at least one real root.
Signs of the Roots
Now, let us understand how to find the signs of the roots of a quadratic equation, using the signs of the coefficients. This is called the Sign Method. It can be pretty handy in objective type questions.
We will consider the quadratic equation a$x^2$ + bx + c = 0 (where a ≠ 0). Make sure that a is positive. If it’s not, then multiply the equation by -1 and make it positive.
Now, four cases are possible when it comes to the signs of b and c.
Case 1: b+, c+
If both b and c are positive, then both the roots will be negative.
For example, have a look at the graph of the quadratic equation $x^2$ + 4x + 3 = 0.
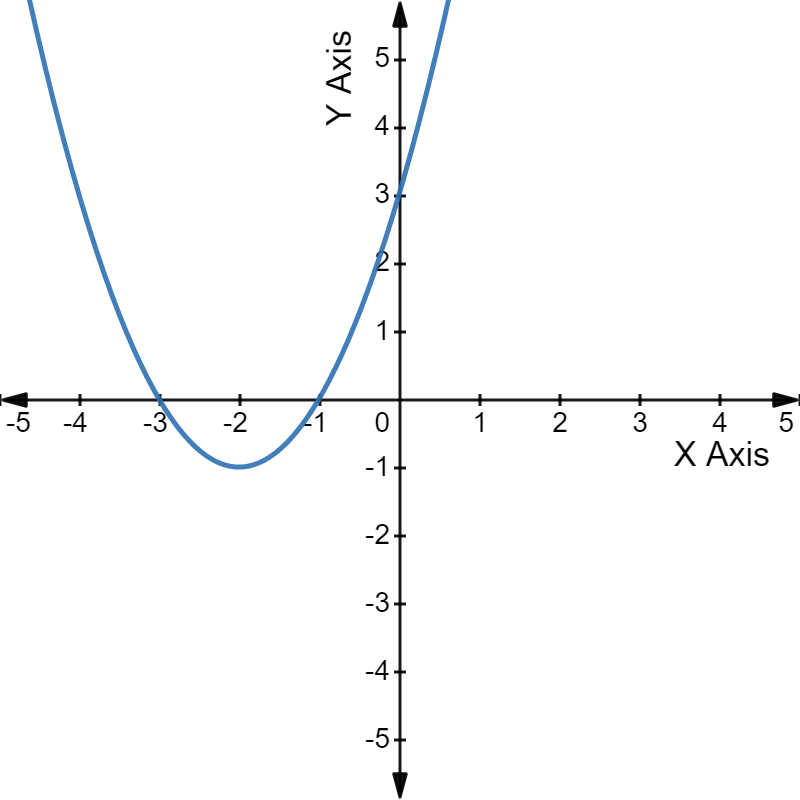 The parabola intercepts the X-axis at -1 and -3, the two roots of the given equation.
The parabola intercepts the X-axis at -1 and -3, the two roots of the given equation.
Case 2: b-, c-
If both b and c are negative, then:
- one root will be positive (the bigger number)
- one root will be negative (the smaller number)
For example, have a look at the graph of the quadratic equation $x^2$ - 2x - 3 = 0.
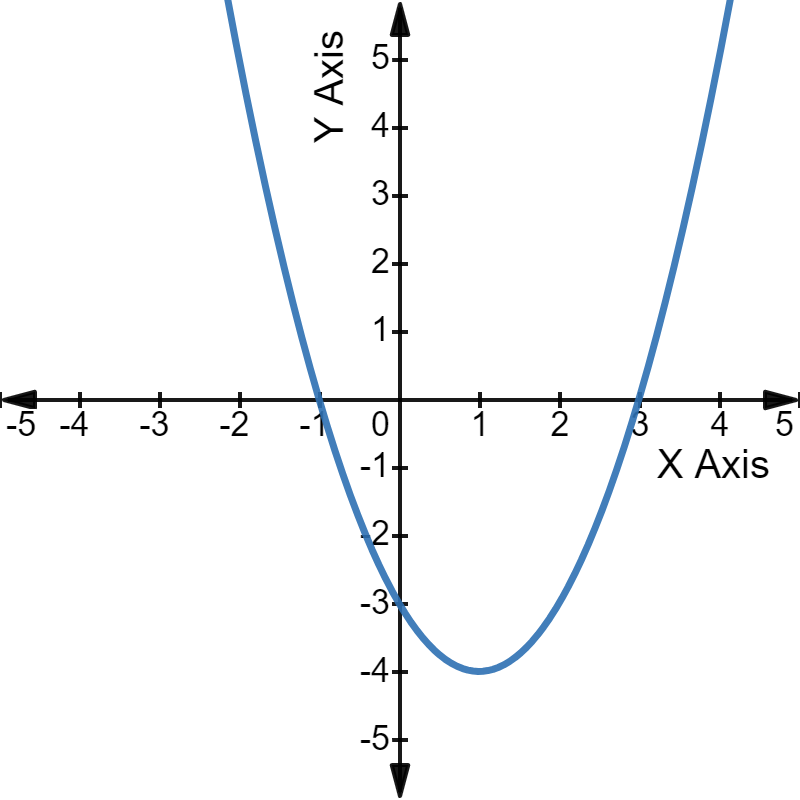 The parabola intercepts the X-axis at -1 and 3, the two roots of the given equation.
The parabola intercepts the X-axis at -1 and 3, the two roots of the given equation.
Case 3: b+, c-
If b is positive and c is negative, then:
- one root will be positive (the smaller number)
- one root will be negative (the bigger number)
For example, have a look at the graph of the quadratic equation $x^2$ + 2x - 3 = 0.
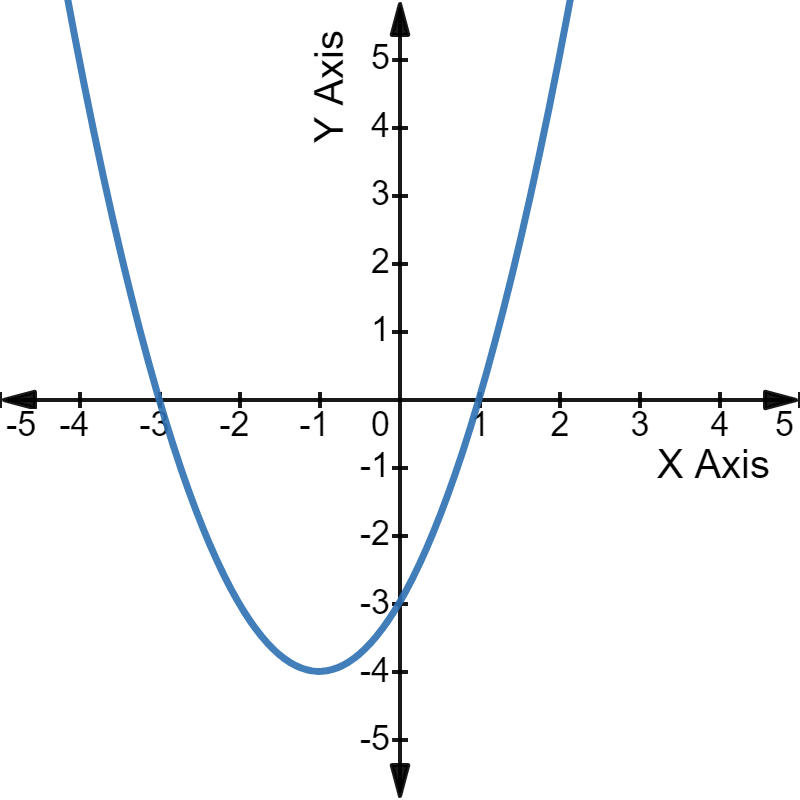 The parabola intercepts the X-axis at 1 and -3, the two roots of the given equation.
The parabola intercepts the X-axis at 1 and -3, the two roots of the given equation.
Case 4: b-, c+
If b is negative and c is positive, then both the roots will be positive.
For example, have a look at the graph of the quadratic equation $x^2$ - 5x + 6 = 0.
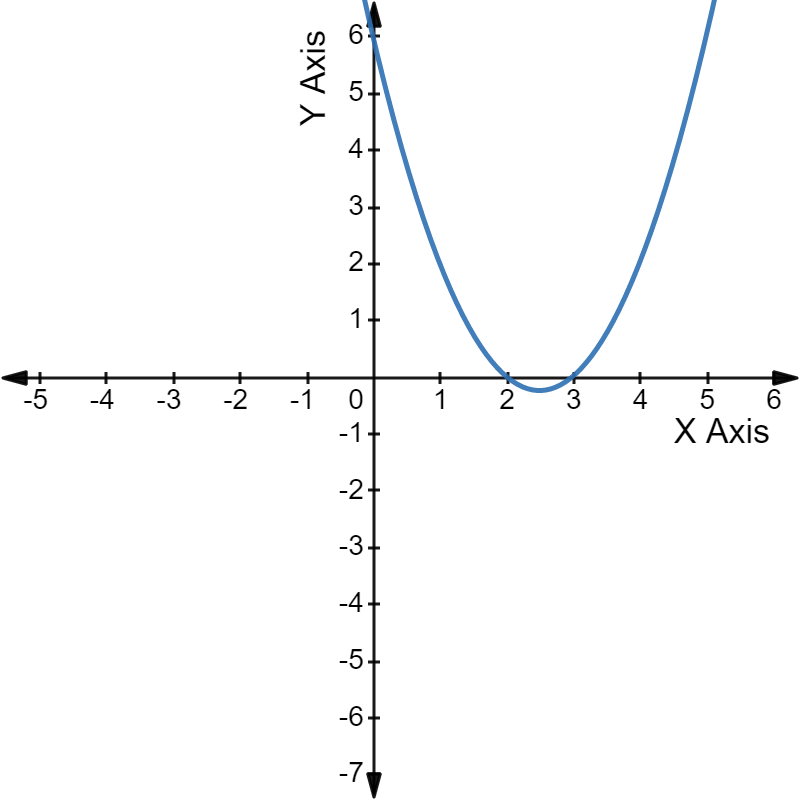 The parabola intercepts the X-axis at 2 and 3, the two roots of the given equation.
The parabola intercepts the X-axis at 2 and 3, the two roots of the given equation.
To summarize:
| Co-efficient of x (b) | Constant (c) | Root α | Root β |
|---|---|---|---|
| Positive | Positive | - | - |
| Negative | Negative | + (bigger number) | - (smaller number) |
| Positive | Negative | + (smaller number) | - (bigger number) |
| Negative | Positive | + | + |
How to find the Roots of a Quadratic Equation?
To find the roots of a quadratic equation, write it in the form a$x^2$ + bx + c = 0 (where a ≠ 0). Make sure that a is positive. If it’s not, then multiply the equation by -1 and make it positive.
Now two cases may arise.
Case 1: a = 1
If the coefficient of $x^2$, i.e. a = 1, then our task is pretty simple.
Step 1: Find two numbers, m and n, such that the product of these two is equal to c and their sum is equal to b. (While doing so, we will consider the signs too)
Step 2: Now, we can rewrite the equation as: (x + m) (x + n) = 0. So, our roots are -m and -n.
Case 2: a > 1
In such a case, follow the following steps:
Step 1: Multiply the constant term c with a. Now, find two numbers, m and n, such that the product of these two is equal to (c × a) and their sum is equal to b. (While doing so, we will consider the signs too)
Step 2: Now, we can rewrite the equation as: (x + m/a) (x + n/a) = 0. So, our roots are -m/a and -n/a.
Let us see some examples to make this concept clearer.
Q. Find the roots of the equation $x^2$ + 4x + 3 = 0
Explanations :
Given equation: $x^2$ + 4x + 3 = 0
So, a = 1; b = 4 and c = 3
As both b and c are positive, both of the roots of this equation must be negative.
Step 1: We will find two numbers, such that their product is equal to c (i.e. 3) and their sum is equal to b (i.e. 4).
We can see that: 1 × 3 = 3, and 1 + 3 = 4Step 2: So, we can rewrite the given equation as: (x + 1)(x + 3) = 0.
So, our roots will be -1 and -3.
 The parabola intercepts the X-axis at -1 and -3, the two roots of the given equation.
The parabola intercepts the X-axis at -1 and -3, the two roots of the given equation.Given equation: $x^2$ + 4x + 3 = 0
So, a = 1; b = 4 and c = 3
We know that, roots of a quadratic equation = $\frac{-b ± \sqrt{b^2 - 4ac}}{2a}$ = $\frac{-4 ± \sqrt{4^2 - 4 × 1 × 3}}{2 × 1}$
= $\frac{-4 ± \sqrt{16 - 12}}{2}$ = $\frac{-4 ± \sqrt{4}}{2}$ = $\frac{-4 ± 2}{2}$ = -2 ± 1 = -1 and -3
Q. Find the roots of the equation 2$x^2$ - 17x + 30 = 0
Explanations :
Given equation: 2$x^2$ - 17x + 30 = 0
So, a = 2; b = -17 and c = 30
As b is negative, and c is positive, both of the roots of this equation must be positive.
Step 1: We will find two numbers, such that their product is equal to c × a (i.e. 30 × 2 = 60) and their sum is equal to b (i.e. -17).
We can see that: (-5) × (-12) = 60, and (-5) + (-12) = -17Step 2: So, we can rewrite the given equation as: (x - 5/2)(x - 12/2) = 0, or (x - 2.5)(x - 6) = 0
So, our roots will be 2.5 and 6.
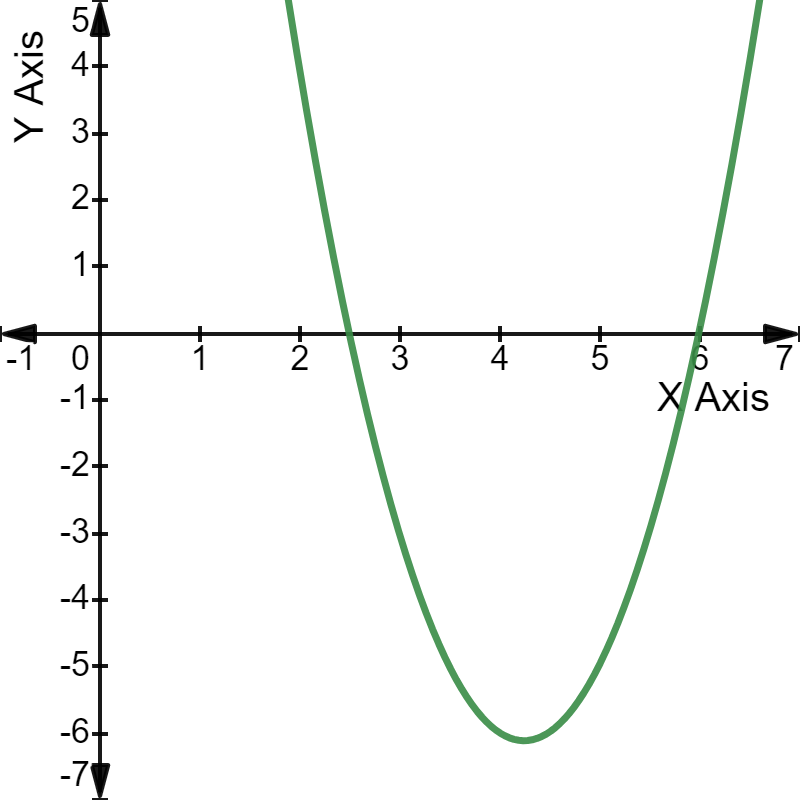 The parabola intercepts the X-axis at 2.5 and 6, the two roots of the given equation.
The parabola intercepts the X-axis at 2.5 and 6, the two roots of the given equation.Given equation: 2$x^2$ - 17x + 30 = 0
So, a = 2; b = -17 and c = 30
We know that, roots of a quadratic equation = $\frac{-b ± \sqrt{b^2 - 4ac}}{2a}$ = $\frac{17 ± \sqrt{(-17)^2 - 4 × 2 × 30}}{2 × 2}$
= $\frac{17 ± \sqrt{289 - 240}}{4}$ = $\frac{17 ± \sqrt{49}}{4}$ = $\frac{17 ± 7}{4}$
= 24/4 and 10/4, i.e. 6 and 2.5