Area of a Triangle

What is Area?

Area of a plane figure is the amount of surface enclosed within its boundary lines. It is expressed in square units e.g. square meter, square centimeter, square inch, etc.

In case of a triangle, it is the amount of surface enclosed within its three boundary lines.

What is Perimeter?

The perimeter of a plane figure is the total length of its sides.

In case of a triangle, it is the total length of its three sides.

Formulae ralated to Area of a Triangle

There are various formulae to find area of a triangle. Some of them can be applied on any triangle, while others are applicable to only a certain kind of triangle. Let’s see a few of them down below.

Formulae for finding area of any Triangle

If base and height are known

If the length of one of the sides of the triangle, which is the base, is b. And the height of the triangle is h, then: 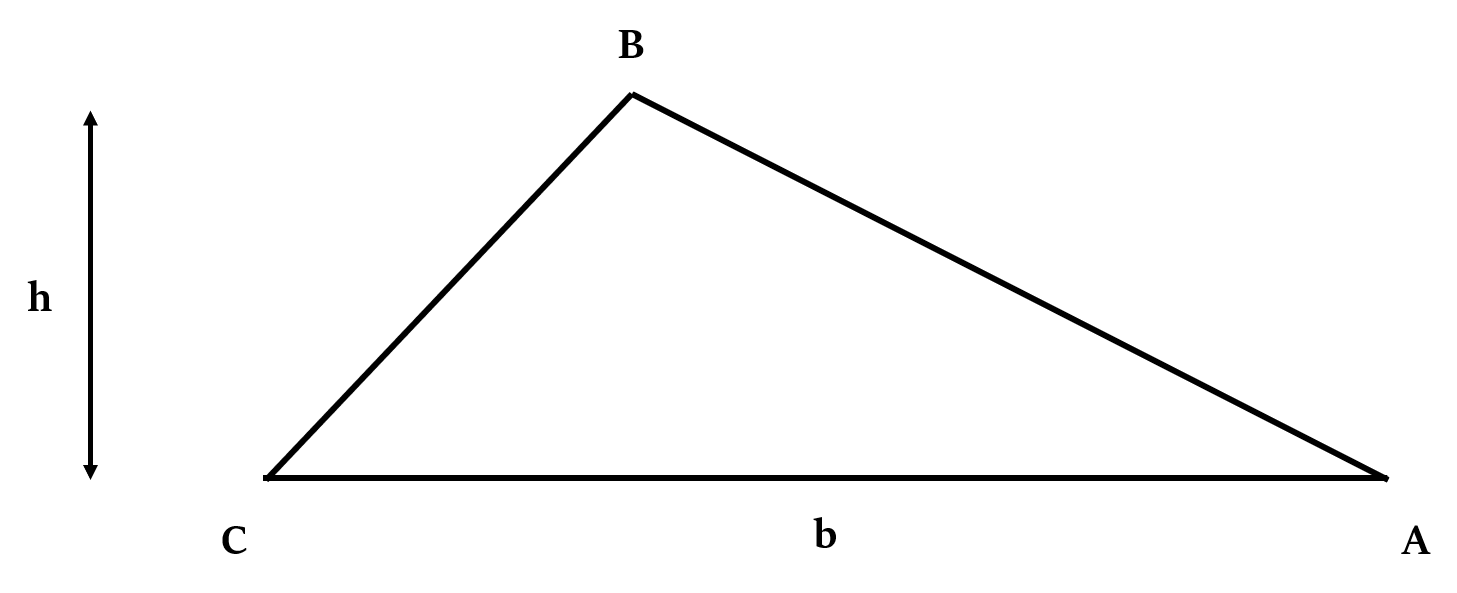Geometry Area of triangle = $\frac{1}{2}$ × base × height = $\frac{1}{2}$ × b × h

Height (h) measured should be perpendicular to the base (b).

In case of a Right Angled triangle, its two sides are already perpendicular to each other (apart from hypotenuse). So, its area = $\frac{1}{2}$ × Product of the sides containing the right angle

If all the three sides are known (Heron’s formula)

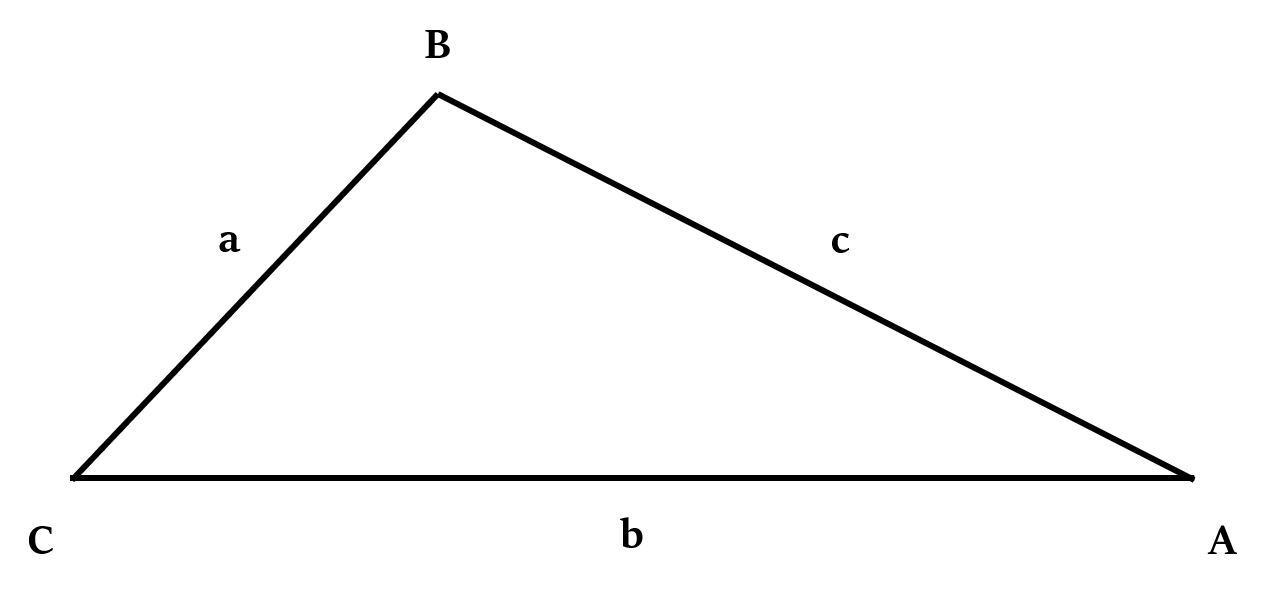If the length of all the three sides of a triangle are known, say a, b and c, then: Geometry Area of triangle = $\sqrt{s (s - a) (s - b) (s - c)}$, where s = $\frac{a + b + c}{2}$

s is the semi-perimeter of a triangle.

If all the three medians are known

If the length of all the three medians of a triangle are known, say p, q and r, then: 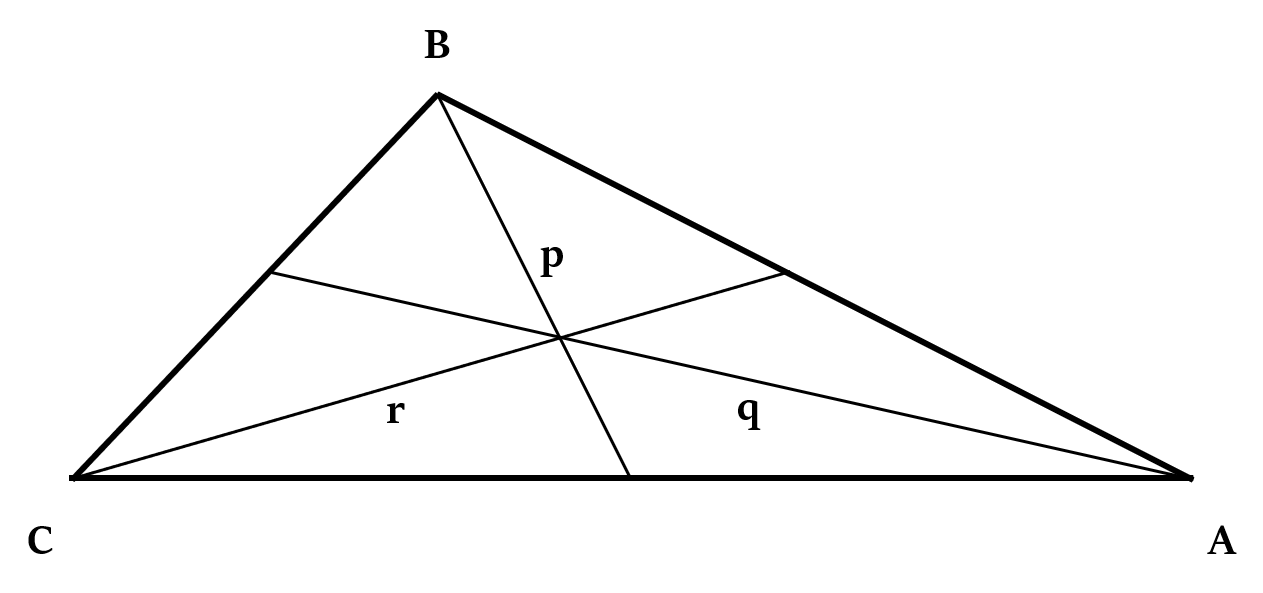Geometry Area of triangle = $\frac{4}{3} \sqrt{z (z - p) (z - q) (z - r)}$, where z = $\frac{p + q + r}{2}$

Formulae for finding area of Equilateral Triangle

We can find the area of an equilateral triangle, if either its side or height is given.

Let’s assume the length of a side of an equilateral triangle to be a, and its height as h.

First of all, let us get to know the relation between side and height of an equilateral triangle.
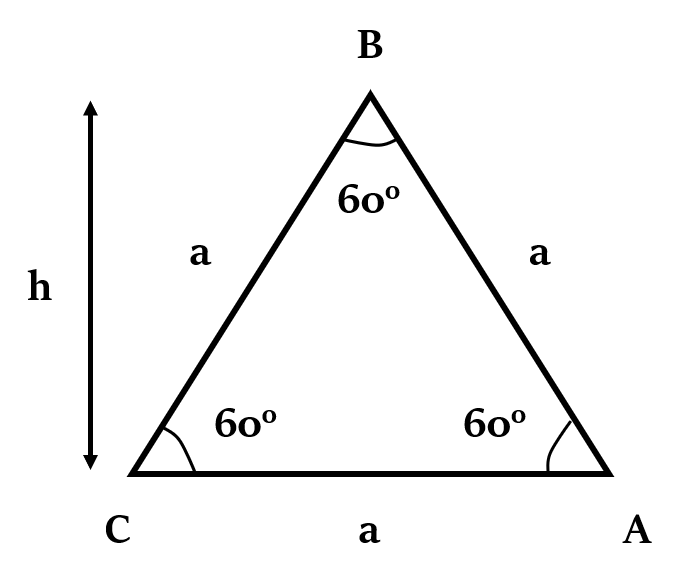Geometry

Height of an equilateral triangle, h = $\frac{\sqrt{3}}{2}$ × a
Or Length of any side of equilateral triangle, a = $\frac{2}{\sqrt{3}}$ × h
(So, in equilateral triangle, Side : Height = 2 : $\sqrt{3}$ )

Area of equilateral triangle = $\frac{\sqrt{3}}{4} × a^2$

Or Area of equilateral triangle = $\frac{h^2}{\sqrt{3}}$

Formulae for finding area of Isosceles Triangle

In an isosceles triangle, two sides are equal.

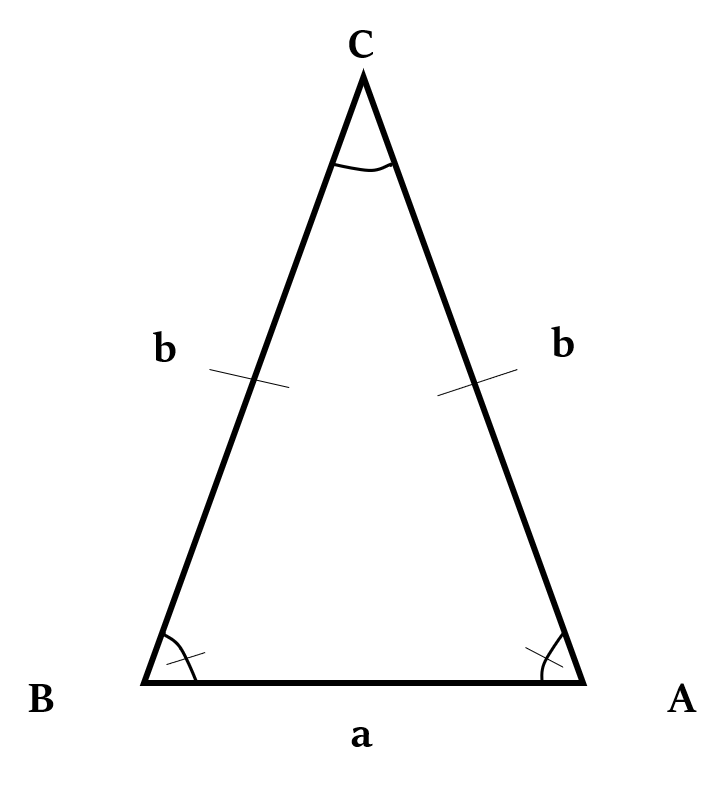
Let the two equal sides be of length b, and the third side be of length a. Geometry

Area of isosceles triangle = $\frac{a}{4} \sqrt{4b^2 - a^2}$

Height of isosceles triangle = $\frac{1}{2} \sqrt{4b^2 - a^2}$

Properties ralated to Area of a Triangle

Property 1

If we join the midpoints of the sides of a triangle, we get four congruent triangles, each of which is similar to the original bigger triangle. 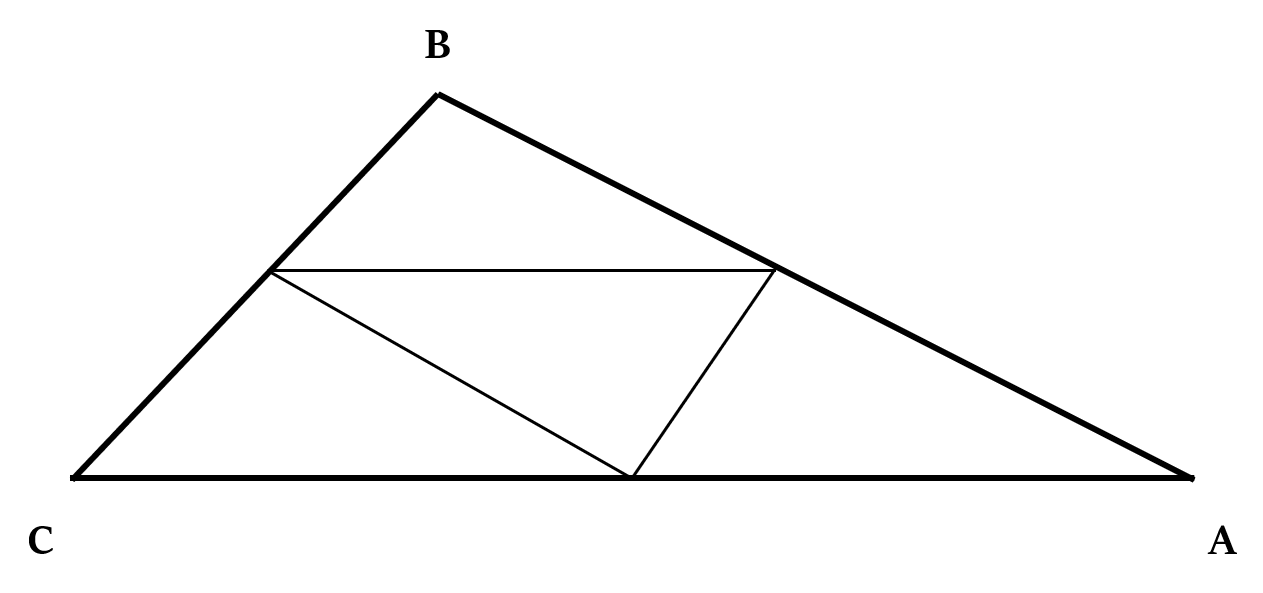Geometry All the four small triangles are equal in area.

Area of each of these small triangles (formed by joining the mid-points of sides) = $\frac{1}{4}$ × Area of the original triangle

Property 2

If two triangles have the same base (or same base length), and are between the same parallel lines (i.e. their height is the same), then their area will be equal. 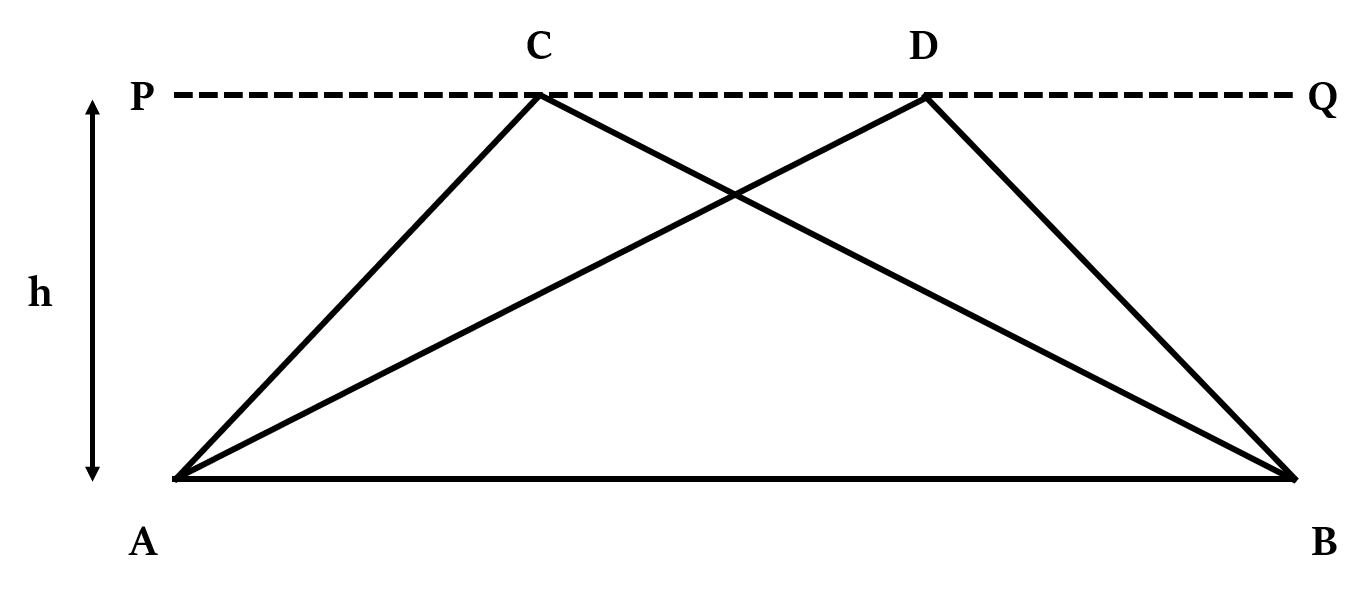Geometry If AB ∥ PQ, then, Area of ∆ABC = Area of ∆ABD

This is because area of a triangle is half of the product of its base and height. If heights of two triangles are the same and the length of their bases too (as is the case above), then they obviously will have the same area.

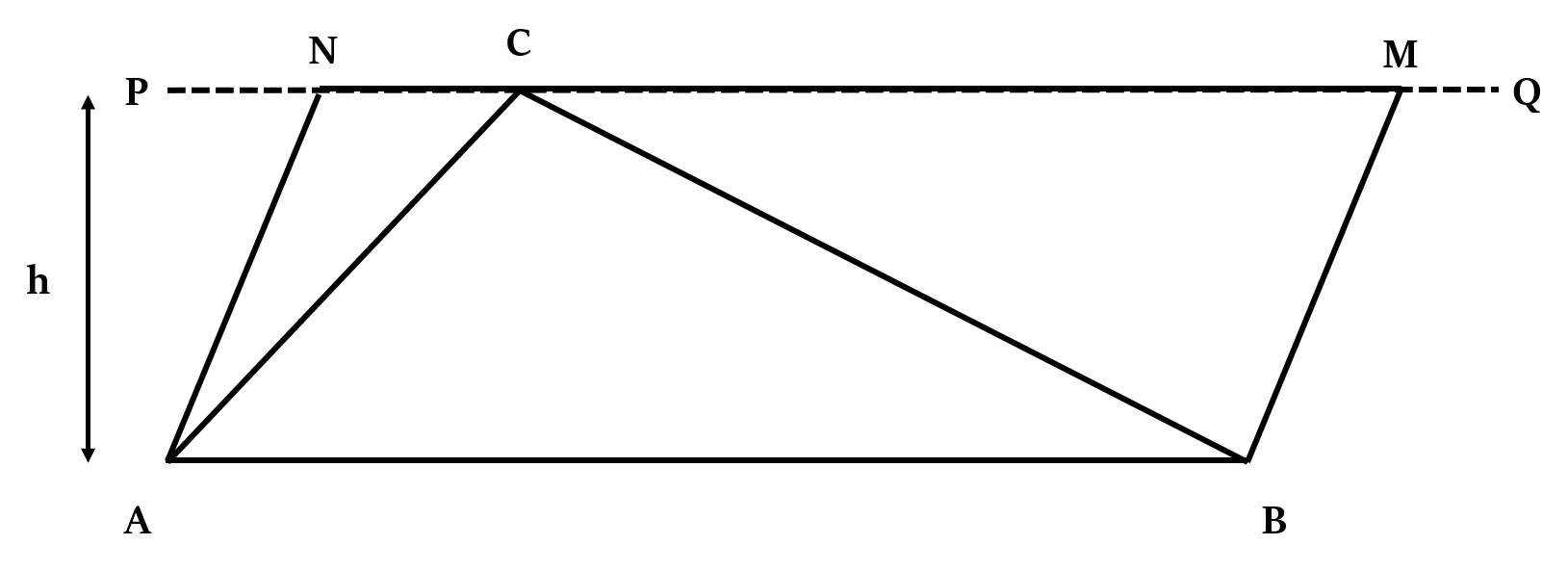If a triangle and a parallelogram have the same base (or same base length), and are between the same parallel lines (i.e. their height is the same), then the area of the triangle will be half of area of the parallelogram. Geometry

If AB ∥ PQ, then, Area of ∆ABC = $\frac{1}{2}$ × Area of parallelogram ABMN

Property 3

If we drop a line from any vertex of a triangle onto the opposite side, then it obviously will divide the original triangle into two parts, as shown below: 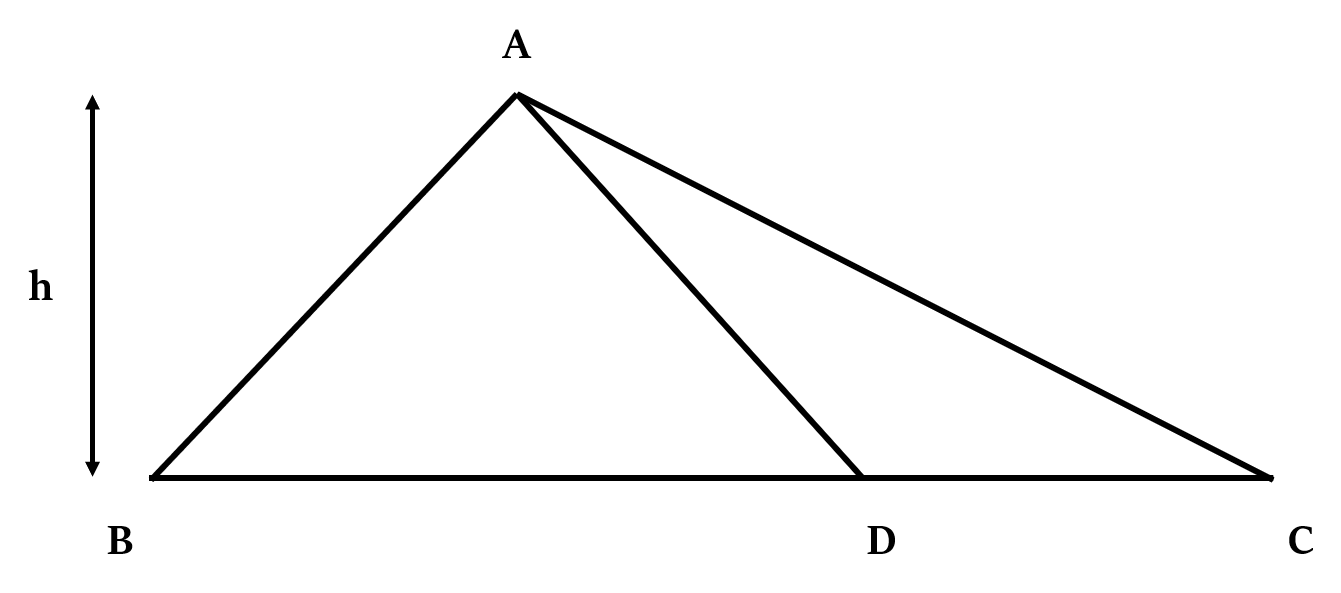Geometry The ratio of the area of these two triangles will be equal to the ratio between their bases.
That is, $\frac{Area \hspace{1ex} of \hspace{1ex} ∆ABD}{Area \hspace{1ex} of \hspace{1ex} ∆ADC}$ = $\frac{BD}{DC}$

For Example, Median of a triangle will divide it into two triangles having equal area.

This is because area of a triangle is half of the product of its base and height. If heights of two triangles are the same (as is the case above), then their area will be in the same ratio as their bases.

Property 4: Maximum Possible Area

Property 4a

If you are given the perimeter of a triangle, then what kind of a triangle will you draw so that it has the maximum possible area?

The answer is equilateral triangle.

In other words, if two or more triangles have the same perimeter, then the equilateral triangle will have the maximum area. 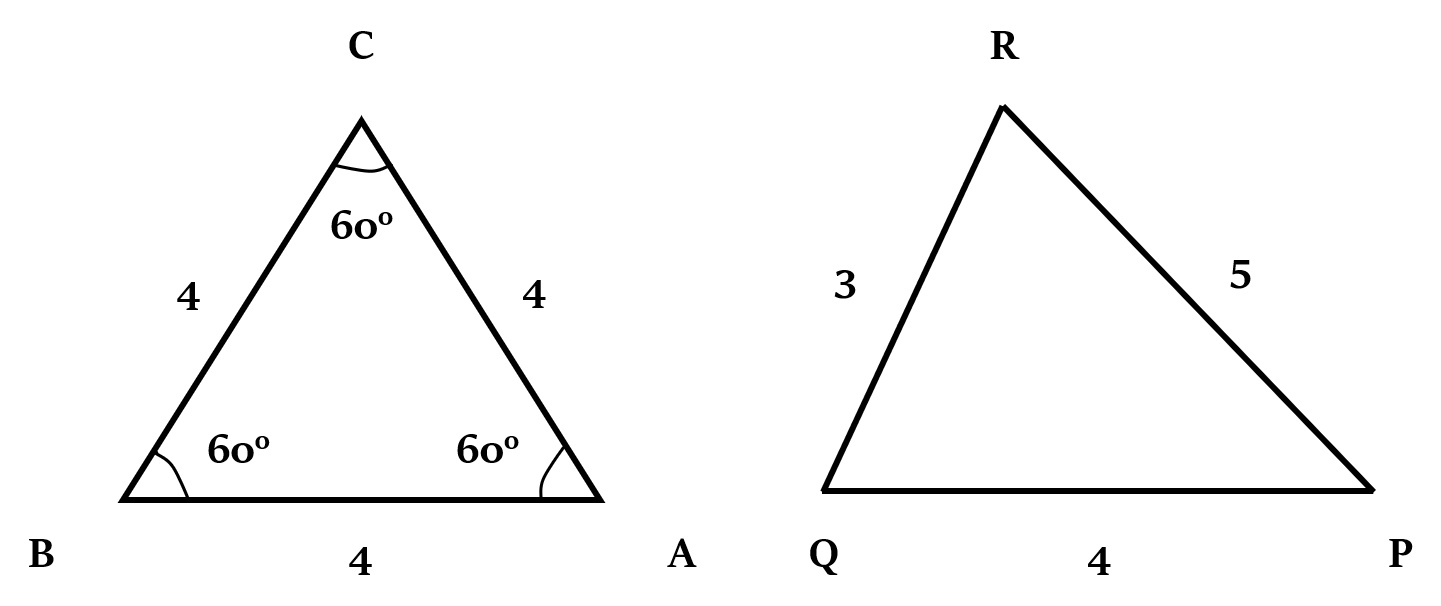Geometry Area of ∆ABC > Area of ∆PQR

Property 4b

If you are given a circle, then what kind of a triangle will you draw inside it, so that it has the maximum possible area?

The answer is again the same - equilateral triangle.

In other words, if two or more triangles are inscribed in a circle, then the equilateral triangle will have the maximum area.

Share on:

Last updated on Jan 18, 2022