Cutting a Cube/Cuboid

Number of smaller cubes

(Finding the number of smaller cubes when a bigger cube or cuboid is cut)

When we cut a rod once, then it divides into how many parts?
When we cut a rod once, then it gets divided into two equal parts.

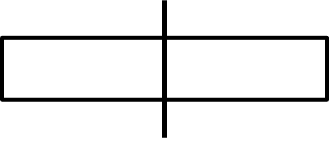
Similarly, if we cut a rod twice, then it divides into three equal parts. 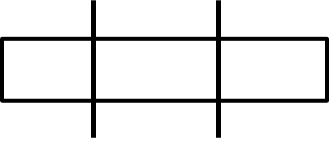And so on…

Can we generalize?
If number of cuts = (n -1), then number of parts in which a rod or a line gets divided into = n

A cube can also be cut as a rod/stick/line.
If a cube of X cm long sides is cut into equal smaller cubes of sides Y cm, then n = X/Y
(n is the number of smaller cubes on each edge.)

If these cuts are made along all the three dimensions, i.e. along the length, breadth and height, then we will get smaller cubes of same size.

Total number of such smaller cubes = $n^3$

Q. If the edge of a cube is 10 cm and it has to be cut into smaller cubes each having edge of 2 cm, then:

1. Each edge of the cube has to be cut how many times?
2. Whole cube will has to be cut how many times?
3. What is the number of smaller cubes thus obtained?

Explanation:

Number of smaller cubes on each edge, i.e. n = X/Y = 10/2 = 5, i.e. each edge has to be divided into 5 parts. (here X = 10 and Y = 2).
And to divide into five parts, each edge will have to be cut 5-1 = 4 times Hence, the number of times the cube has to be cut = 4×3 = 12
Number of smaller cubes = $n^3$ = $5^3$ = 125 (Basically, it’s length × breadth × height)

What if it’s a cuboid?
Can we still count the number of smaller cubes?
When a cuboid is cut into smaller cubes of equal volume, then:
Total number of Cubes = $ \frac{Vol. \hspace{1ex} of \hspace{1ex} Cuboid}{Vol. \hspace{1ex} of \hspace{1ex} smaller \hspace{1ex} cube} $ = $ \frac{Length × Breadth × Height \hspace{1ex} of \hspace{1ex} cuboid}{(Side \hspace{1ex} of \hspace{1ex} smaller \hspace{1ex} cubes)^3} $

Let’s consider an example.

Q. If a cuboid with length = 10 cm, breadth = 8 cm and height = 6 cm is cut into smaller cubes of edge 2 cm each, then find the number of smaller cubes.

 (a) 72  (b) 42  (c) 48  (d) 60 

Explanations :
1 2

Q. How many cubes are there in this cuboid?

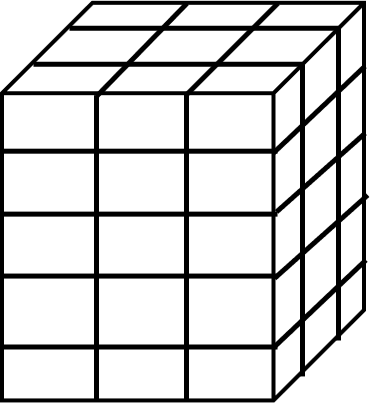
Explanation:

Types of smaller cubes

After cutting a cube, following four types of smaller cubes are obtained:
(we are taking an example of a cube where there are 3 cubes on each of its edges, i.e. n = 3)

Corner cubes

Cubes at the middle of each edge

Number of middle cubes = 12 (n - 2)
OR
Number of middle cubes = Number of middle cubes on each edge × 12 (as there are 12 edges in a cube) In this case, Number of middle cubes = 12 (n - 2) = 12 (3 - 2) = 12

Cubes at the centre of each face

Number of such cubes = 6 $(n – 2)^2$
OR
Number of such cubes = Number of middle cubes in each face × 6 (as there are 6 faces in a cube) 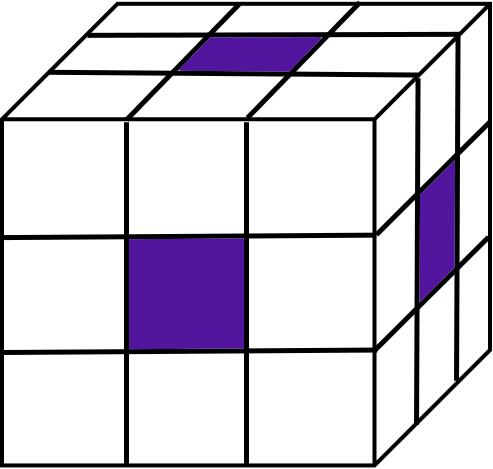In this case, such cubes = 6 $(3 - 2)^2$ = 6

Inner cubes that are hidden

Number of inner cubes = $(n - 2)^3$ In this case, such cubes = $(n - 2)^3$ = $(3 - 2)^3$ = 1

Q. If a larger cube of 8 cm edge is cut into smaller cubes of equal volumes, each having edge of 2 cm, then:

Number of smaller cubes = ?
Number of corner cubes = ?
Number of cubes at the centre of edges = ?
Number of cubes at the centre of faces = ?
Number of inner cubes (N) = ?

Explanation:

Q. A cube of side 4 cm is painted blue on all of its surfaces and then divided into various smaller cubes of side 1 cm each. Find the number of cubes having none, one, two and three faces painted.

Explanation:

For those who are more into mugging up the numbers, here’s a list of the number of four types of smallers cubes/blocks (got after cutting bigger cubes of various sizes):

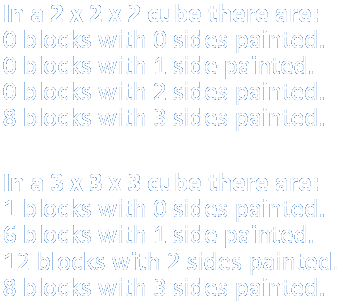
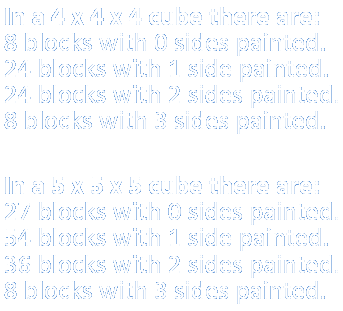
Note: We will solve questions wherein the larger cube is painted with more than one colours and then cut, in a separate module. Here we covered the basics of cutting and painting a cube.