Types of Permutation Questions
In this article, we will have a look at the various types of questions that we encounter based on the topic of Permutation.
But you must be aware of the basic concepts of Permutation before we do so. If you aren’t, then have a look at the previous articles.
Type 1: Arranging all n distinct items
Type 1a: Selecting and then Arranging (Without any Condition)
Q. How many eight letter words (meaningful or meaningless) in English can be formed that have 2 different vowels and 6 different consonants?
(a) $C^5_2$ × $C^{21}_6$ × 2! × 6!
(b) $P^5_2$ × $P^{21}_6$
(c) $C^5_2$ × $C^{21}_6$ × 8!
(d) $C^{26}_8$ × 8!
Explanation:
First step will be to select:
English language has 5 vowels and 21 consonants.
2 vowels can be chosen in $C^5_2$ ways and 6 consonants may be chosen in $C^{21}_6$ ways.
Now, these eight letters may be rearranged in 8! ways.
Total number of words that can be formed = $C^5_2$ × $C^{21}_6$ × 8!
Answer: (c)
Type 1b: Selecting and then Arranging (With some Conditions)
Q. In how many ways can we seat 5 men and 3 women in a row, so that women occupy the odd places?
(a) 24 (b) 2880 (c) 120 (d) 1440
Explanation:
The odd places are: 1, 3, 5, 7
We need to select 3 places out of these 4, and then arrange the women amidst them.
Number of ways to select 3 places out of 4 = $C^4_3$ = 4
Number of ways to arrange the women in these 3 places = 3! = 6
So, total number of ways in which women may be selected and then arranged = 4 × 6 = 24
We can fill the remaining 5 places with 5 men
Number of ways to select 5 places out of 5 = $C^5_5$ = 1
Number of ways to arrange the men in these 5 places = 5! = 120
So, total number of ways in which men may be selected and then arranged = 1 × 120 = 120
Hence, the total number of ways in which these men and women can be arranged = 24 × 120 = 2880
Answer: (b)
Q. How many 3-digit natural numbers (without repetition of digits) are there such that each digit is odd and the number is divisible by 5 ?
(a) 8 (b) 12 (c) 16 (d) 24
Explanation:
We need to find three-digit numbers in which:
- All digits are different, and all digits are odd. So, the three digits must be from amongst 1, 3, 5, 7, and 9.
- The number is divisible by 5, i.e. the units digit is 5.
The number of ways we can fill the first two digits from amongst 4 distinct digits = 4 × 3 = 12.
Answer: (b)
Type 1c: Just Arranging required (Without any Condition)
Q. In how many different ways can the letters of the word LUCKNOW be rearranged to generate different words (meaningful or meaningless), such that all the letters are utilized?
(a) 7! (b) 24 (c) 720 (d) 120
Explanation:
Total number of alphabets available = 7 (‘L’, ‘U’, ‘C’, ‘K’, ‘N’, ‘O’, and ‘W’)
Total number of permutations possible = 7!
Answer: (a)
Type 1d: Just Arranging required (With some Conditions)
Q. The letters of the word LUCKNOW are rearranged to generate all possible words (meaningful or meaningless). In the list of all the words generated, how many words have the word ‘NOW’ embedded in them?
(a) 7! (b) 24 (c) 720 (d) 120
Explanation:
The word ‘NOW’ has to appear in the word. So, we can assume that ‘NOW’ is a single alphabet and the remaining alphabets ‘L’, ‘U’, ‘C’ and ‘K’ are re-arranged along with ‘NOW’ to generate all possible words.
Total number of alphabets available = 5 (‘L’, ‘U’, ‘C’, ‘K’ and ‘NOW’)
Total number of permutations possible = 5! = 120.
Answer: (d)
Q. In how many ways can 6 rods of different colours be arranged in a row, such that the saffron and the red rods are never together?
(a) 480 (b) 240 (c) 720 (d) 120
Explanation:
Total number of different rods available = 6
So, Total number of permutations possible = 6! = 720.
Now, we will use the tactic of eliminating the unwanted cases. We do not want rods of saffron and red colours to be together. So, we will find out the number of cases where they are together, and then subtract them from all possible cases.
We can group red and saffron rods together. So, now we are left with 5 distinct rods. We can arrange them in 5! ways.
Red and saffron rods are together, and so they can be arranged in 2! ways.
Hence, Number of cases in which saffron and red rods are together = 5! × 2! = 120 × 2 = 240
So, number of all possible cases wherein the saffron and the red rods are not together = Total number of permutations possible - Number of cases in which saffron and red rods are together = 720 - 240 = 480
Answer: (a)
Type 1e: Placing distinct objects in boxes
Q. In how many ways can we place 6 distinct balls into 3 boxes?
(a) $3^3$
(b) $6^3$
(c) $6^6$
(d) $3^6$
Explanation:
Each of the 6 distinct balls can be put in any of the 3 boxes. So, the first ball can be put in 3 ways. The second ball can be put in 3 ways. And so on.
So, the total number of ways in which 6 distinct balls can be put in 3 boxes = 3 × 3 × 3 × 3 × 3 × 3 = $3^6$
Answer: (d)
Q. In how many ways can we place 6 distinct balls into 3 boxes, so that no two boxes remain empty?
(a) $3^6$ - 6
(b) $6^3$ - 1
(c) $3^6$ - 2
(d) $3^6$ - 3
Explanation:
Each of the 6 distinct balls can be put in any of the 3 boxes. So, the first ball can be put in 3 ways. The second ball can be put in 3 ways. And so on.
So, the total number of ways in which 6 distinct balls can be put in 3 boxes = 3 × 3 × 3 × 3 × 3 × 3 = $3^6$
Two boxes will remain empty if we put all the balls in a single box. So, there are 3 such cases:
- When all the balls are put in the first box.
- When all the balls are put in the second box.
- When all the balls are put in the third box.
So, the total number of ways in which 6 distinct balls can be put in 3 boxes, such that no two boxes remain empty = $3^6$ - 3
Answer: (d)
Q. There are 4 people in a lift. They can get out of the lift at any floor from 1 to 5. In how many ways can these people get off the lift?
(a) $4^5$
(b) $5^4$
(c) $5^5$
(d) $4^4$
Explanation:
Each of the 4 persons can leave the lift at any of the 5 floors. So, the first person can leave the lift in 5 ways. The second person can also leave the lift in 5 ways. And so on.
So, the total number of ways in which 4 persons can get off the lift = 5 × 5 × 5 × 5 = $5^4$
Answer: (b)
Q. In how many ways can 3 letters be put in 4 letter boxes?
(a) $3^3$
(b) $3^4$
(c) $4^3$
(d) $4^4$
Explanation:
Each of the 3 letters can be put in any of the 4 letter boxes. So, the first letter can be put in any of the 4 letter boxes. The second letter can be put in any of the 4 letter boxes. And so on.
So, the total number of ways in which 3 letters can be put in 4 letter boxes = 4 × 4 × 4 = $4^3$
Answer: (c)
Q. There are 5 objective questions in a mini-test, each having 4 options. In how many ways can a student answer these questions, if all questions have to be attempted?
(a) $4^5$
(b) $5^4$
(c) $5^5$
(d) $4^4$
Explanation:
Each of the 5 objective questions can be answered in 4 ways. So, the first question can be answered in 4 ways. The second question can be answered in 4 ways. And so on.
So, the total number of ways in which 5 objective questions can be answered = 4 × 4 × 4 × 4 × 4 = $4^5$
Answer: (a)
Q. If we write numbers from 1 to 999, then how many times will the digit 8 appear?
(a) 200 (b) 300 (c) 250 (d) 350
Explanation:
Any number from 1 to 999 can be represented as xyz, i.e. as a three-digit number, wherein 0 ≤ x, y, z ≤ 9
Now three cases may arise:
Case 1: 8 appears only once
So, we need to choose one place out of the three, where we can put 8. This can be done in $C^3_1$ = 3 ways
The rest of the two places can be filled in 9 ways each (as only 9 digits are left, if we leave out the digit 8).
So, total number of such numbers = 3 × 9 × 9 = 243
As 8 appears only once in these numbers, the number of occurances of 8 = 243
Case 2: 8 appears twice
So, we need to choose two places out of the three, where we can put 8. This can be done in $C^3_2$ = 3 ways
The remaining one place can be filled in 9 ways (as only 9 digits are left, if we leave out the digit 8).
So, total number of such numbers = 3 × 9 = 27 ways
As 8 appears twice in these numbers, the number of occurances of 8 = 2 × 27 = 54
Case 3: 8 appears thrice
This can be done only in one way, i.e. 888
As 8 appears thrice in it, the number of occurances of 8 = 3
So, the number of times the digit 8 will appear from 1 to 999 = 243 + 54 + 3 = 300
Answer: (b)
Type 1f: Questions having At least and At most
In questions having at least or at most, we use the concept of elimination. It makes our calculation pretty easy.
- Step 1: Find all the possible cases.
- Step 2: Find all the unwanted cases.
- Step 3: Subtract all the unwanted cases from the total possible cases.
Q. In how many ways can 4 die be rolled, such that at least one dice shows 2?
(a) $6^4 - 5^4$
(b) $5^4 - 6^4$
(c) $4^6 - 4^5$
(d) $6^4$ - 6
Explanation:
A dice can be rolled in 6 ways. So, the total number of ways in which 4 die can be rolled = 6 × 6 × 6 × 6 = $6^4$
We want at least one dice to show 2. So, we should eliminate all those cases wherein no dice showed 2.
Now, the total number of ways in which these 4 die can be rolled, such that no die turns up 2 = 5 × 5 × 5 × 5 = $5^4$
So, the total number of ways in which these 4 die can be rolled, such that at least one dice shows 2 = $6^4 - 5^4$
Answer: (a)
Q. In how many ways can we make 3-letter words out of the 9 different letters provided to us, such that at least one letter is repeated?
(a) 504 (b) 250 (c) 729 (d) 225
Explanation:
The total number of ways in which 3-letter words can be made out of 9 different letters = 9 × 9 × 9 = $9^3$ = 729
We want at least one letter to repeat. So, we should eliminate all those cases wherein no letter is repeated.
Now, the total number of ways in which 3-letter words can be made, such that no letter is repeated = 9 × 8 × 7 = 504
We can also calculate the above as follows:
- Select 3 different letters out of 9: $C^9_3$
- Arrange these 3 letters: 3!
So, the total number of ways in which 3-letter words can be made, such that no letter is repeated = $C^9_3$ × 3! = 9 × 8 × 7 = 504
So, the total number of ways in which 3-letter words can be made, such that at least one letter is repeated = 729 - 504 = 225
Answer: (d)
Type 2: Arranging some distinct and some identical items
Q. In how many ways can the letters of the word ALPHA be arranged such that both As are never together?
(a) 60 (b) 24 (c) 36 (d) 120
Explanation:
Number of permutations of n objects out of which p, q and r are of different types = $\frac{n!}{(p! q! r!)}$
ALPHA has 5 alphabets of which 2 are of the same type, i.e. two A’s.
Total number of possible arrangements in the word ALPHA = 5!/2! = 60.
When both As come together, the two A can be treated as single and in that case, it can be considered a case of 4 alphabets, where all are distinct.
Total number of possible arrangements when both As are together = 4! = 24
Total number of permutations when A’s are apart = Total number of permutations possible – Total number of permutations when A’s are together = 60 - 24 = 36
Answer: (c)
Miscellaneous Questions
Q. There are 9 cups placed on a table arranged in equal number of rows and columns out of which 6 cups contain coffee and 3 cups contain tea. In how many ways can they be arranged so that each row should contain at least one cup of coffee?
(a) 18 (b) 27 (c) 54 (d) 81
Explanation:
The cups will be arranged in a 3 × 3 matrix.

Now, let’s consider all the possible cases.
Case 1: Each row has 2 cups of coffee and 1 cup of tea.
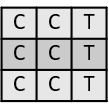
One tea cup can be placed in a row in 3 ways.
So, Possible arrangements wherein all rows have 2 coffee cups= 3 × 3 × 3 = 27 ways
Case 2: One row has 3 cups of coffee.
In such a case, one of the rows will have 2 cups of coffee and the other will have 1 cup of coffee.
If the first row has 3 coffee cups, then the possible arrangements = 3 × 3 = 9 ways
The rows having 3, 2 and 1 coffee cups can be arranged in 3! = 6 ways
So, Possible arrangements wherein one row has 3 coffee cups = 9 × 6 ways = 54 ways
Therefore, total possible arrangements = 27 + 54 = 81 ways
Answer: (d)