Mensuration - Tetrahedron

What is a Tetrahedron?

A tetrahedron is a triangular pyramid, i.e. all of its faces are triangles, including the base polygon.

Types of Tetrahedrons

Tetrahedrons can be classified based on various parameters.

Classification based on Faces

Regular Tetrahedron - if all of the four faces of a tetrahedron are equilateral triangles.
Irregular Tetrahedron - these are the tetrahedrons that are not regular tetrahedrons.

Equi-triangular Tetrahedron - if base of a tetrahedron is an equilateral triangle and the other triangular faces are congruent (exactly same) isosceles triangles. It is a type of irregular tetrahedron.

Classification based on Position of Apex

Right tetrahedrons - if apex of a tetrahedron is directly above the center of its base.

A right tetrahedron can be regular (if all the faces are same) or irregular (if all the faces, except the base, are the same).

A regular tetrahedron is always a right tetrahedron.
Oblique tetrahedrons - these are the tetrahedrons that are not right tetrahedrons.

As we will study soon, an oblique tetrahedron is also an irregular tetrahedron.

In fact, whenever we use the word right in front of any kind of pyramid, it means that the apex of that pyramid lies directly above the center of its base.

Now, let’s study about these types of tetrahedrons in more detail.

Regular Tetrahedron

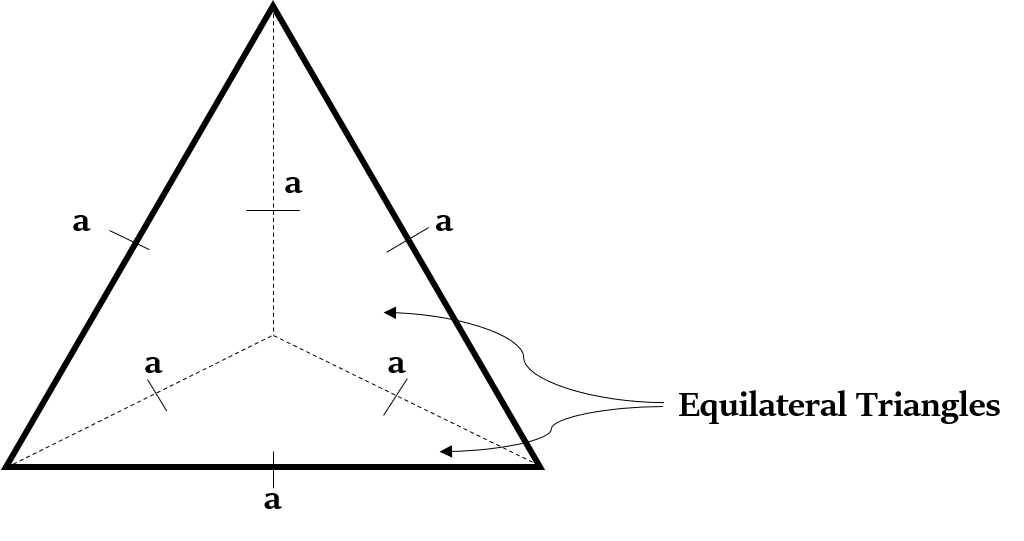
All the four faces of a Regular Tetrahedron are congruent equilateral triangles (including its base). Mensuration

So, length of all of the edges of a Regular Tetrahedron is equal.

Apex of a Regular Tetrahedron is directly above the center of its base. So, all Regular Tetrahedrons are in fact Right Regular Tetrahedrons.

Formula 1: Volume

Volume of a Pyramid = $\frac{1}{3}$ × Base Area × Height

So, Volume of a Right Equi-triangular Tetrahedron = $\frac{1}{3}$ × Base Area × Height = $\frac{1}{3}$ × $\frac{\sqrt{3}}{4} a^2 × \frac{\sqrt{2}}{\sqrt{3}}a$ = $\frac{\sqrt{2}}{12} a^3$

Formula 2: Surface Area

Lateral surface area = Sum of the areas of three congruent equilateral triangles = 3 × $\frac{\sqrt{3}}{4} a^2$

Total surface area = Sum of the areas of four congruent equilateral triangles = 4 × $\frac{\sqrt{3}}{4} a^2$ = $\sqrt{3} a^2$

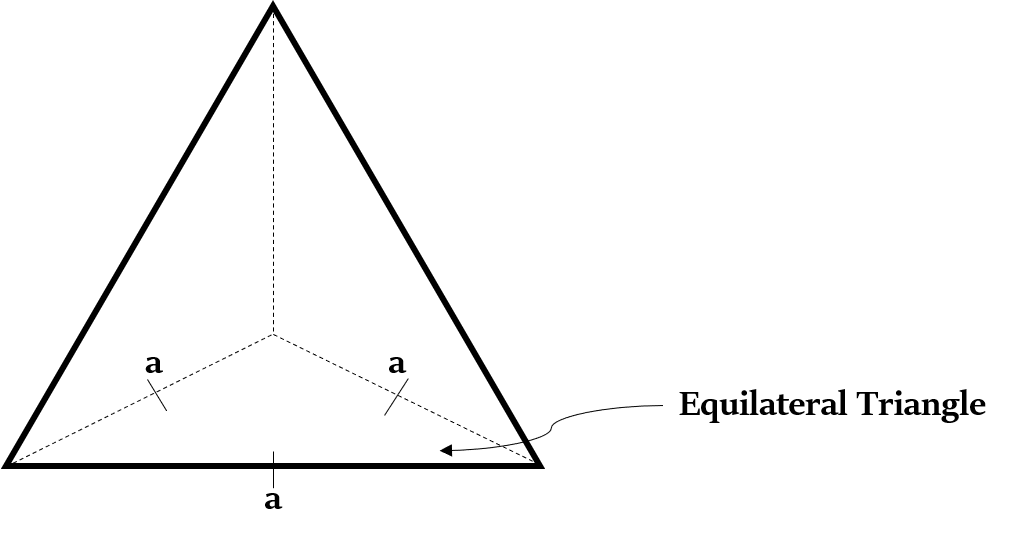
Right Equi-triangular Tetrahedron

Right Equi-triangular Tetrahedron has an equilateral triangle as its base. Rest of its faces are congruent (exactly same) isosceles triangles. So, its apex is directly above the center of its base. Mensuration

Formula 1: Slant Height and Slant Edge

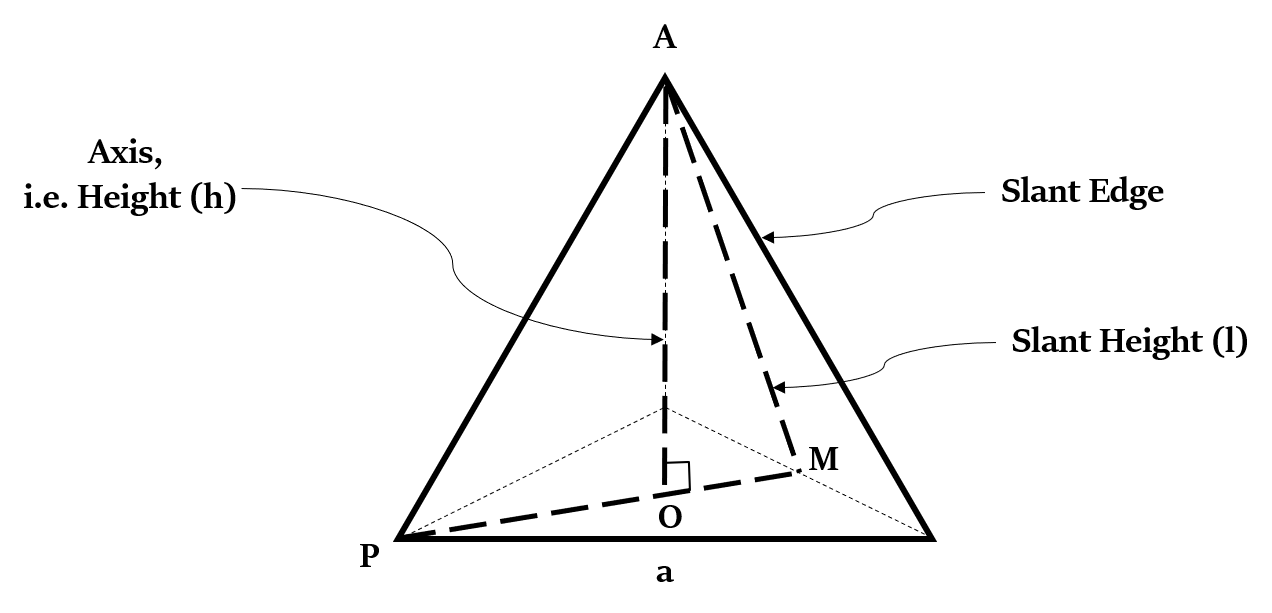
If h - height, r - inradius of the equilateral triangle as the base, R - circumradius of the equilateral triangle as the base. Mensuration

Circumradius of the equilateral triangle as the base, R = $\frac{a}{\sqrt{3}}$
Inradius of the equilateral triangle as the base, r = $\frac{a}{2 \sqrt{3}}$

By Pythagoras theorem:

Slant height, l = $\sqrt{h^2 + r^2}$ = $\sqrt{h^2 + (\frac{a}{2 \sqrt{3}})^2}$

Slant Edge = $\sqrt{h^2 + R^2}$ = $\sqrt{h^2 + (\frac{a}{\sqrt{3}})^2}$

Formula 2: Volume

Volume of a Pyramid = $\frac{1}{3}$ × Base Area × Height

So, Volume of a Right Equi-triangular Tetrahedron = $\frac{1}{3}$ × Base Area × Height = $\frac{1}{3}$ × $\frac{\sqrt{3}}{4} a^2$ × h

Formula 3: Surface Area

Lateral surface area = $\frac{1}{2}$ × Perimeter of base × Slant height = $\frac{1}{2}$ × 3a × l

Total surface area = Lateral surface area + Area of base = $\frac{1}{2}$ × 3a × l + $\frac{\sqrt{3}}{4} a^2$

Share on:

Last updated on Sep 11, 2021