Basics of Functions
What is a Function?
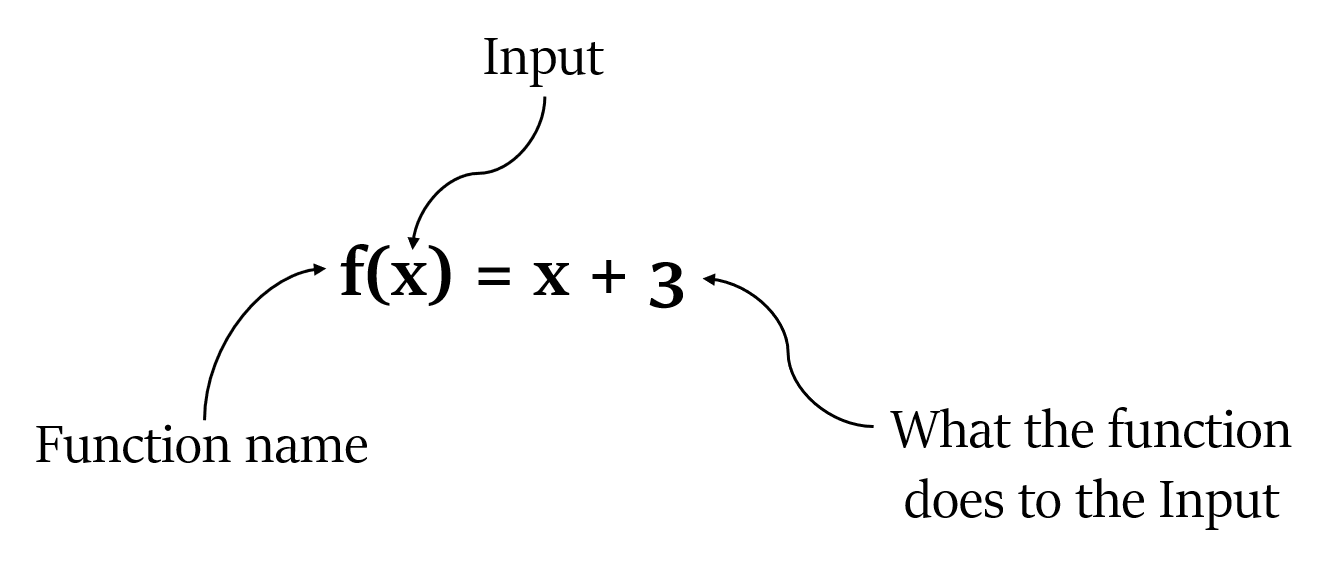
A function is an expression that showcases a relation between an input and an output.
It is often represented by f(x). The input is represented by ‘x’ placed inside the parentheses. What the function does with that input is represented by the expression on the right-hand side of the ‘=’ sign.
For example, f(x) = x + 3. Here, x is the input and x + 3 will be the output.
Say, x = 2 (i.e. the input), then the function ‘f’ will add 3 in that input and provide us the output. So, f(x) = 2 + 3 = 5 (i.e. the output)
So, a function has three main parts:
- input, e.g. x
- relationship, e.g. + 3
- output
Though, by convention, we generally use the letter ‘f’ to denote a function. However, we can name it ‘g’ or anything else too. For example, g(x) = x + 3.
We need not even use any function name. So, we can just write, y = x + 3. Here, ‘x’ is the input, and ‘y’ is the output.
Similarly, ‘x’ also just works as a placeholder. So, instead of ‘x’ we can also use any other letter. For example, f(a) = a + 3. It only serves the purpose of letting us know where to put the values.
Functions and Sets
So, when we deal with functions, we deal with two sets:
- Set of Input values, e.g. 1, 2, 3, 4 etc.
- Set of Output values that the function, f(x) = $x^2$ will generate for the above input values will be: 1, 4, 9, 16 etc.
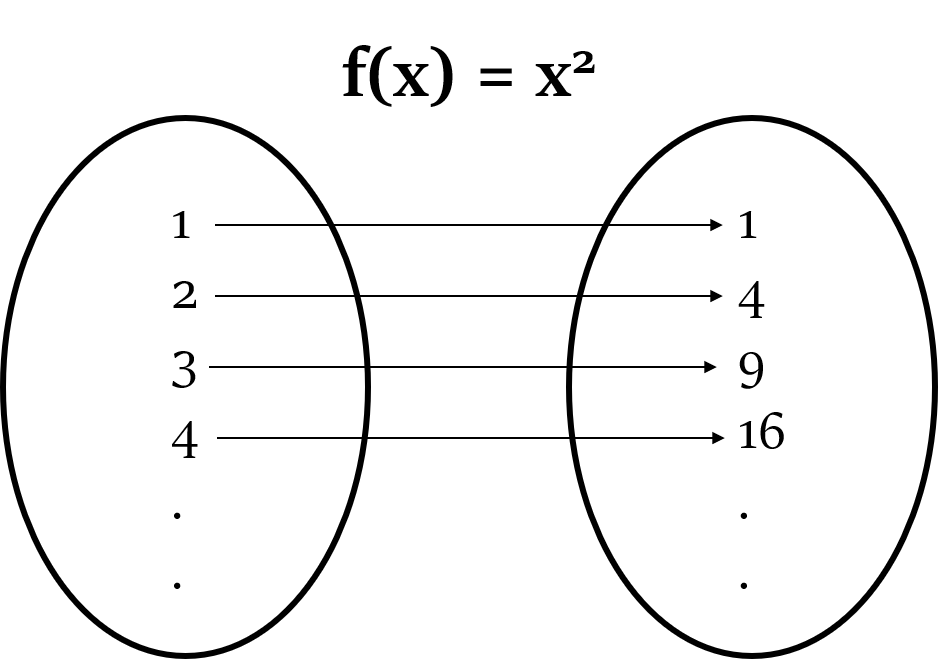
We can represent the input and output of a function as an ordered pair, such that input is written first, followed by the output, i.e. (x, f(x)).
So, a function can also be seen as a set of ordered pairs. For example, the above function f(x) = $x^2$ can also be represented as: (1, 1), (2, 4), (3, 9), etc. These are x and y coordinate points that can easily be plotted on a graph.
Domain, Codomain and Range
You will often encounter these terms in the chapter of Functions - Domain, Codomain, Range, etc. Let’s try to understand these terms.
Have a look at the following representation of a function, showing relationship between the input set and output set.
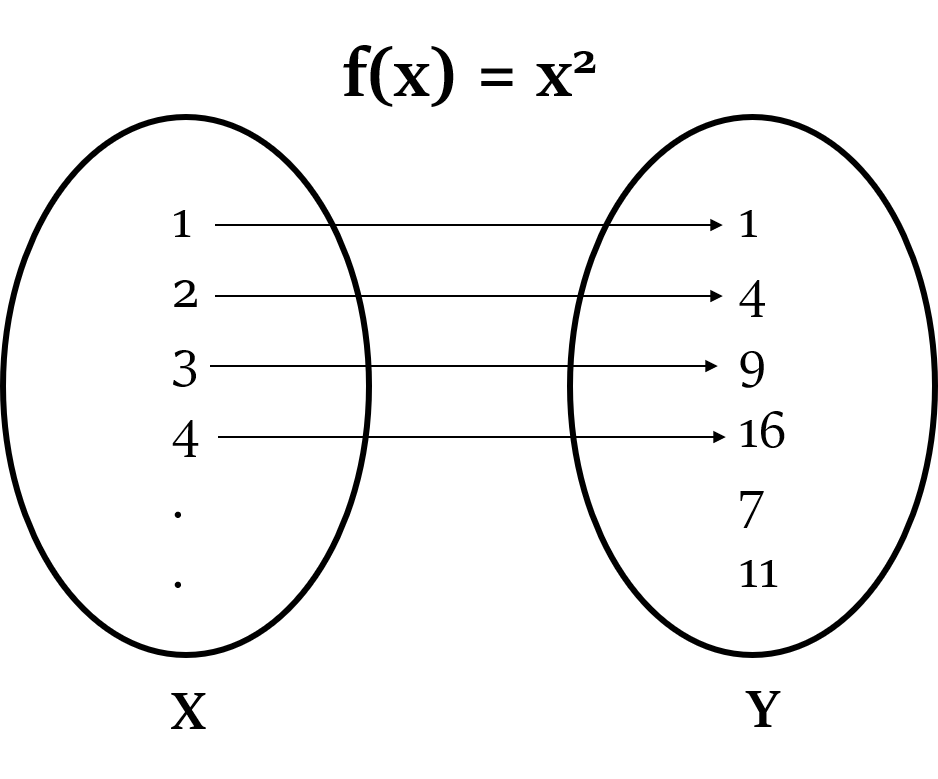
- Set of Input values (1, 2, 3, 4 ….), i.e. X is called the Domain.
- Set of Output values that the function, f(x) = $x^2$ will generate for the above input values (1, 4, 9, 16 …) is called the Range.
- Set Y having all the output values (1, 4, 9, 16 …) and some other values (7, 11 …) is called the Co-Domain.
In functions, we have a lot of names for the same thing.
So, input can also be called as domain, or domain element, independent variable or argument.
Similarly, output can also be called as range, or range element. image, dependent variable, value of a function.
Rules that Functions must fulfil
There are certain rules that a function must fulfil.
- A function must work for any given input value, i.e. every possible input value must have an output value. (One to One relation is allowed)
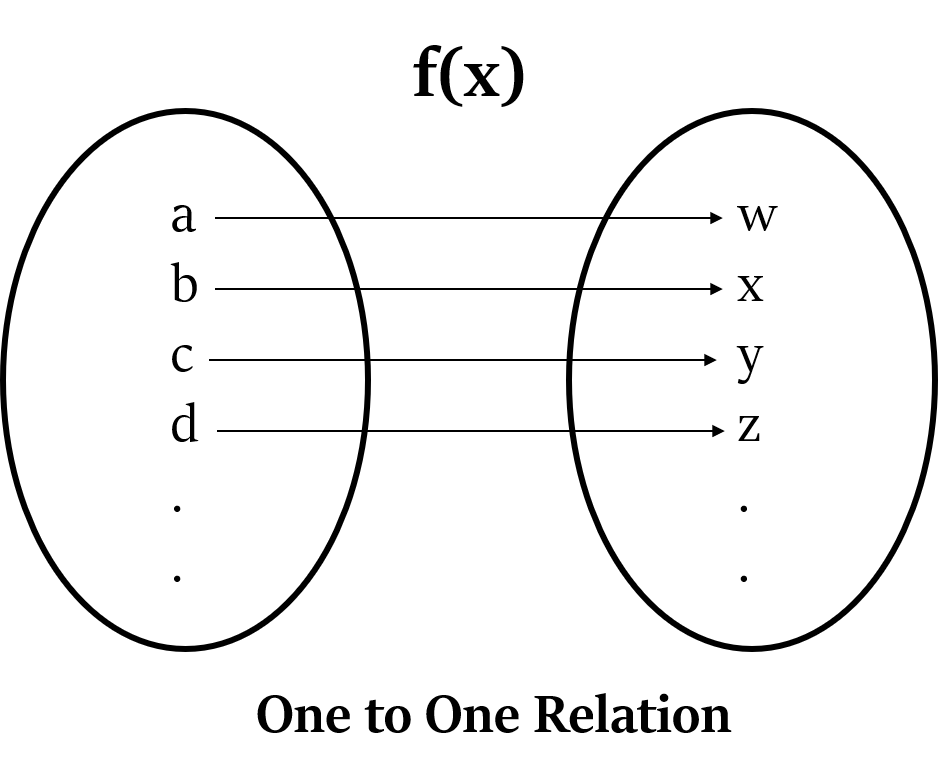
Every input value when entered into a function must produce an output value, i.e. every element in input set is related to an element in output set.
However, some elements in the output set may not be related to any element in the input set. That’s fine.
- A function must have only one relationship for each input value, i.e. for each input value there must be only one output value. (One to Many relation is not allowed)
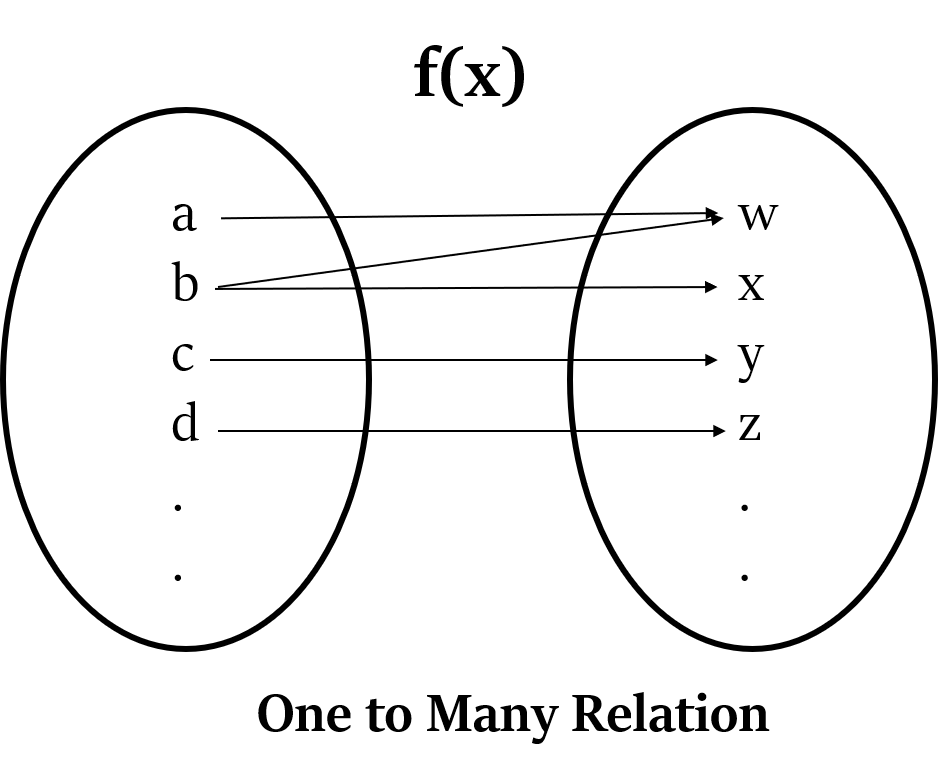
In short, every input value when inserted in a function must provide us exactly one output value. Not zero, not two, only one.
For example, when x = 1, we get f(x) = $x^2$ = $1^2$ = 1
When x = 2, we get f(x) = $x^2$ = $2^2$ = 4
When x = 3, we get f(x) = $x^2$ = $3^2$ = 9
However, two input values may have same output values. That’s fine. (Many to One relation is allowed)
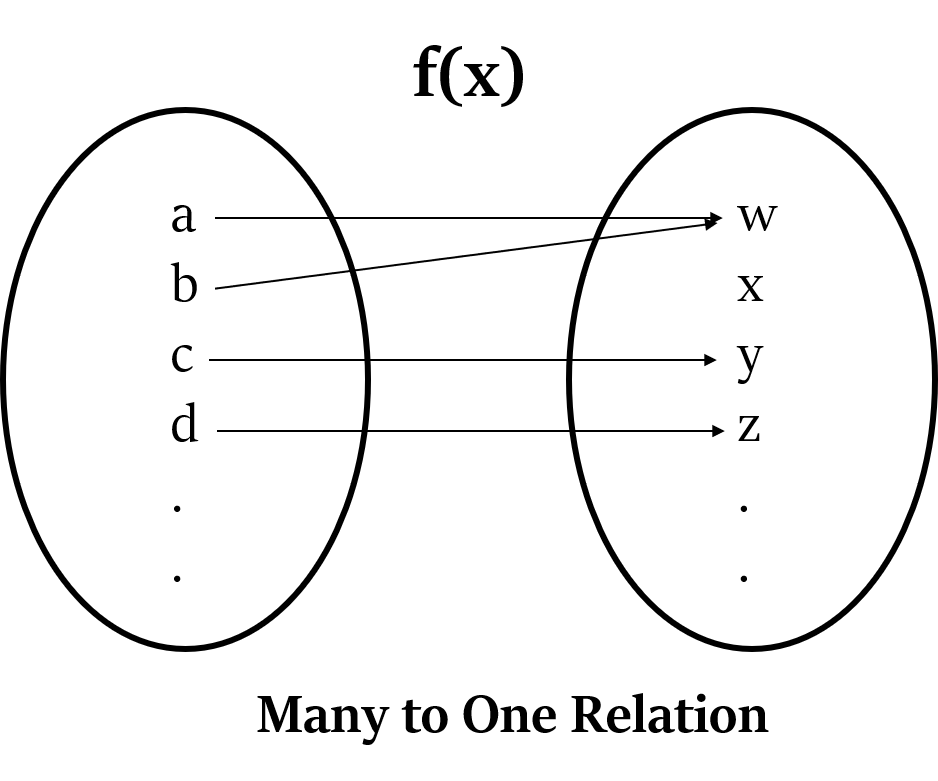
For example, when x = 1, we get f(x) = $x^2$ = $1^2$ = 1
When x = -1, we get f(x) = $x^2$ = $(-1)^2$ = 1
So, we may also define a function as follows:
A function is an expression that showcases a relation between each element of an input set with exactly one element of the output set.
If the above rules are not followed, then a relationship between two sets cannot be called a function. It will just be called a relationship.
For example, consider the diagrams given below representing the relationships between elements of two sets, X and Y.
Relationship 1:
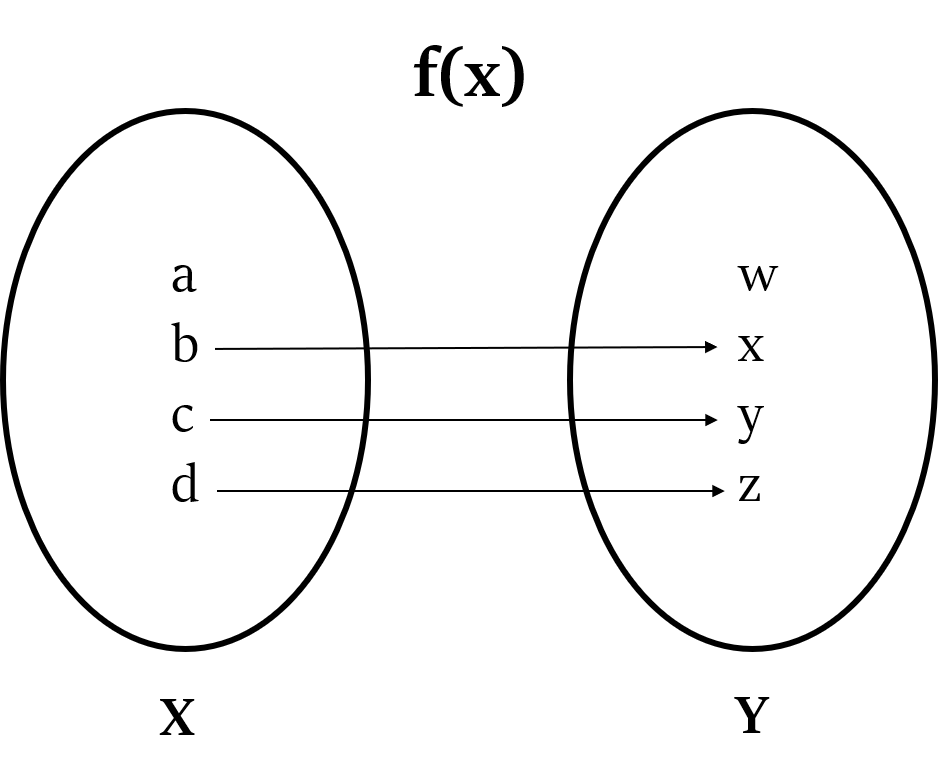
Element ‘a’ in Set X is not related to any element in Set Y. So, this relationship is not a function.
Relationship 2:
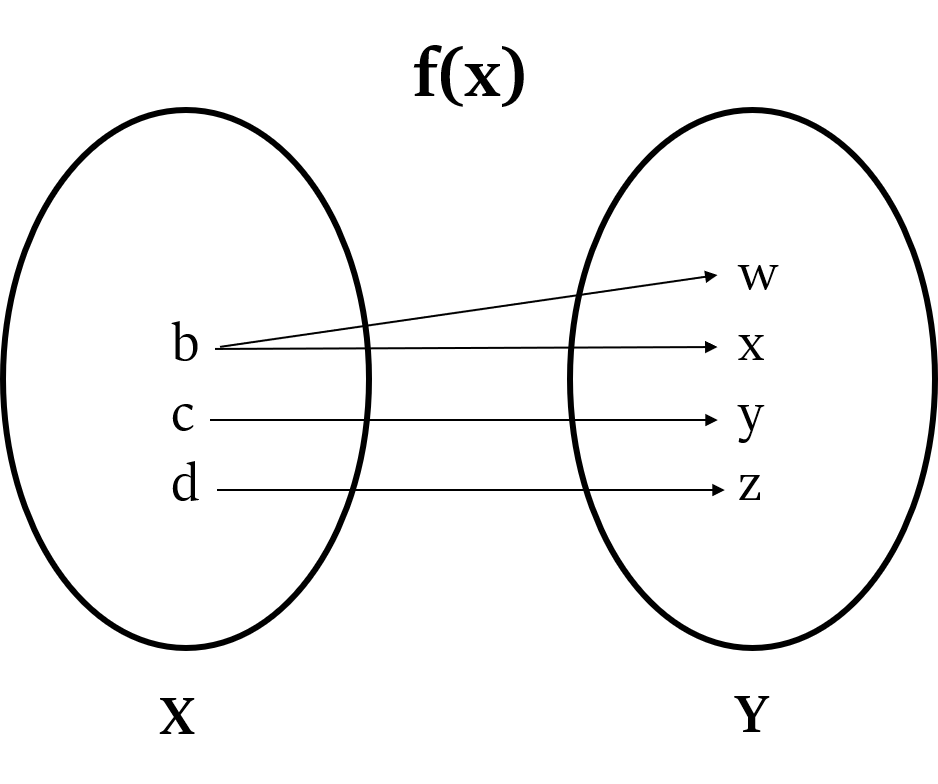
Element ‘b’ in Set X is related to more than one element in Set Y (w and x). So, this relationship is not a function.
An easier way to remember all this is to imagine a mirror.
Any person standing in front of a mirror must have a reflection (i.e. every element in domain must have a related element in co-domain.)
A person standing in front of a mirror must have a single reflection. He cannot have multiple reflections (i.e. every element in domain must have only one related element in co-domain.)
Two persons standing in front of a mirror can look the same (e.g. if they are twins) (i.e. two or more elements in domain can have a single related element in co-domain.)
Vertical Line Test
Another way to check whether an expression is a function or not is to have a look at their graph. As a function provides exactly one output for each input, so it means that a vertical line passing through the X-axis will intercept the curve exactly at one place.
Have a look at the following graph of the function, f(x) = x + 3
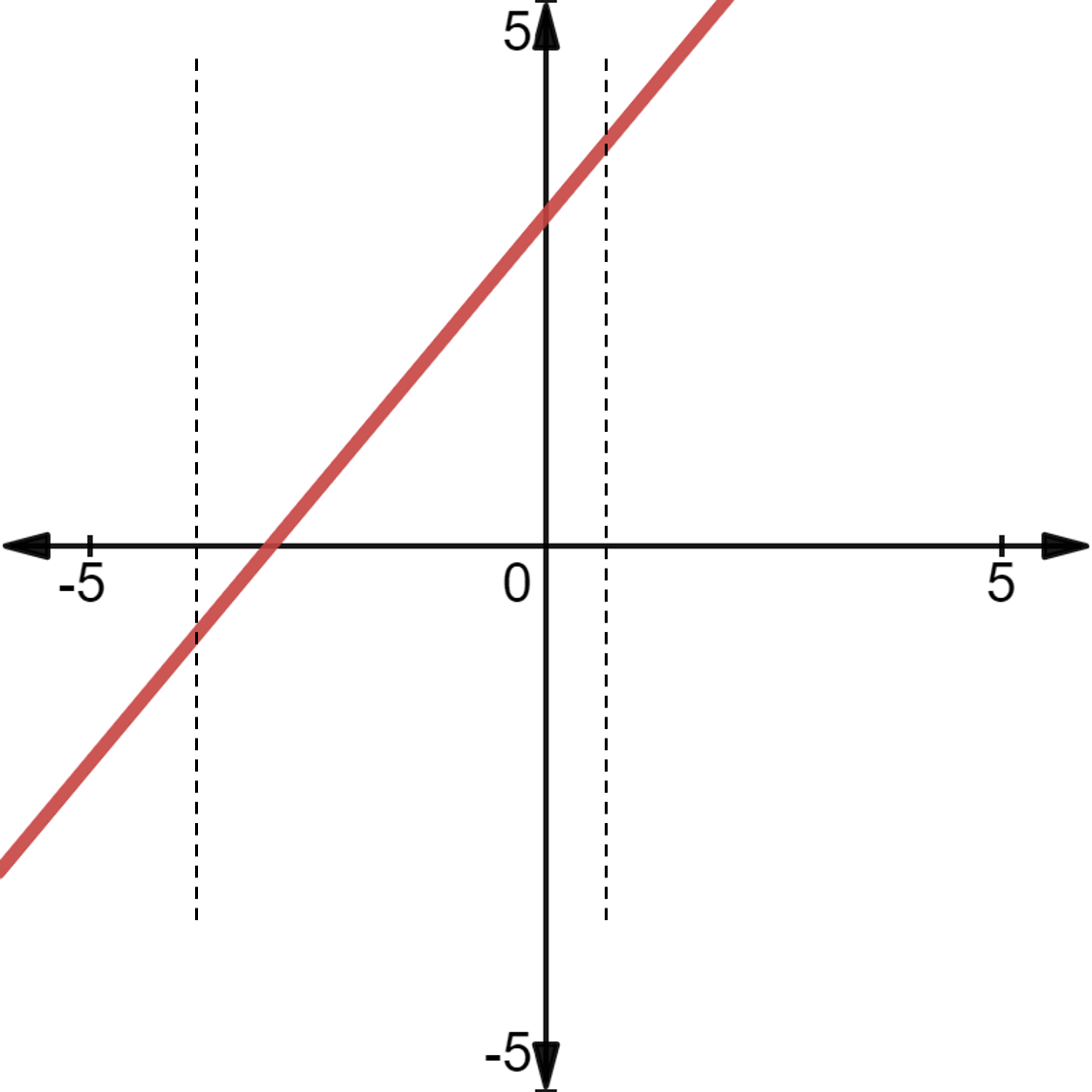
If a vertical line passing through the X-axis intercepts the curve of an expression:
- at more than one points (it means more than one output for a single input), or
- at no point (it means no output for an input), then that expression cannot be a function.
For example, have a look at the following graph:
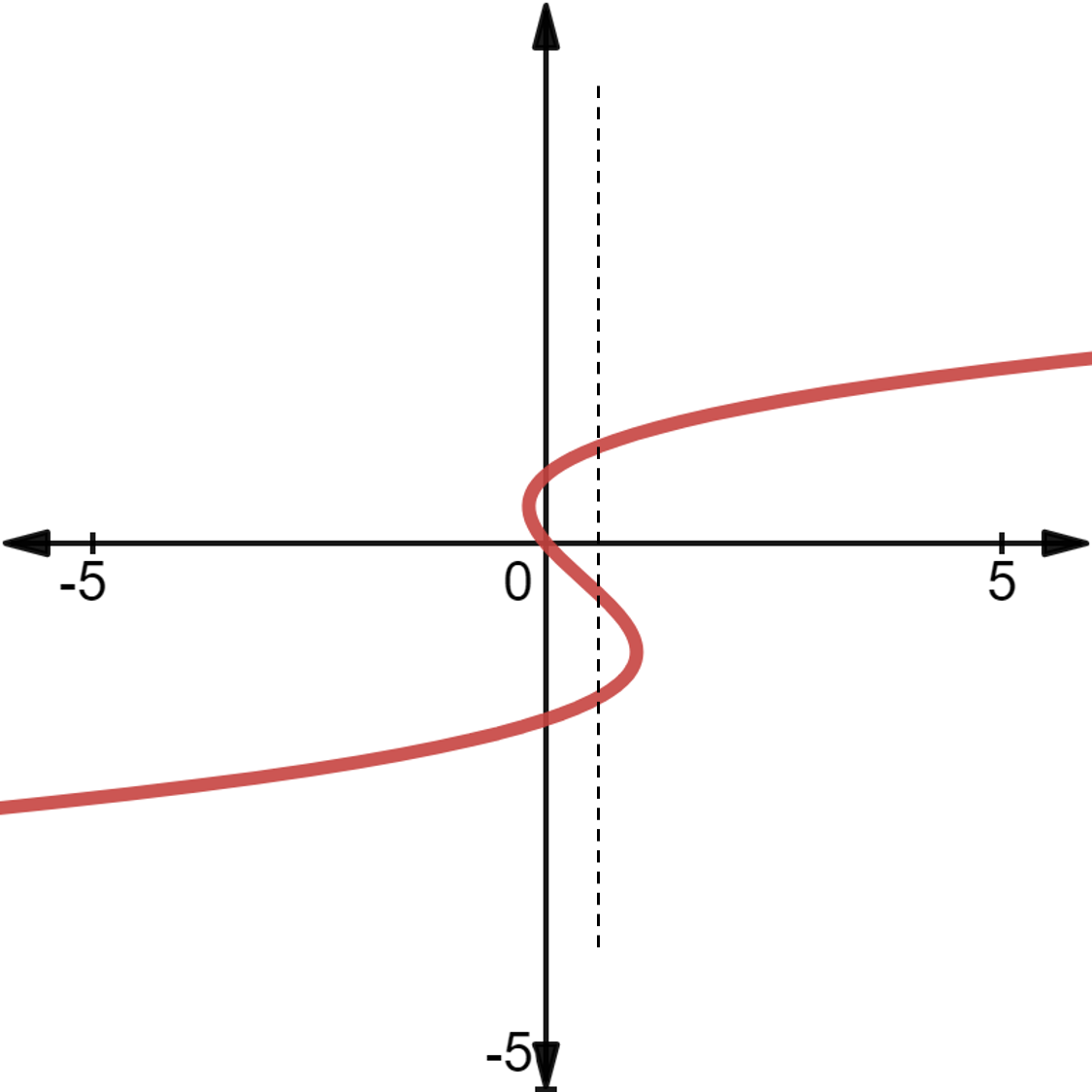
As a vertical line passing through the X-axis intercepts the curve at more than one points, the expression (whose curve has been plotted) cannot be a function.
Some more points to know about a Function
The curve of a function need not be a continuous curve. It may be broken. The only condition is that it must produce exactly one output for every input.
You will generally encounter explicit functions, i.e. where it is pretty clear how to get the output value. For example, y = $x^2$ – 5. However, sometimes you may also come across implicit functions, i.e. where it is not very clear how to find output from input. For example, $x^3$ + 2y – $x^2$ = 0.