Simplification Concepts, Methods and Tricks
In this article, we will learn about the various methods to simplify complex looking mathematical expressions.
BODMAS-based Simplification
The simplest types of simplification questions are based on just the application of BODMAS rule, i.e. our capability to apply addition, subtraction, multiplication, division operations and the use of different brackets in proper order.
So, the first thing we will do is to learn about the BODMAS rule. Most of you must already be aware of it. But you may revise it, if you feel the need.
What is BODMAS rule?
To simplify arithmetic expressions, which involve various operations like addition, division, brackets, etc. we need to follow a pre-determined sequence of operations. That is, there is a hierarchy of arithmetic operations, which is called as the BODMAS rule.
In fact, the word BODMAS is basically an acronym of these operators in a defined order. Let’s see what it stands for.
- B - stands for Brackets. It has the highest hierarchy. So, there are brackets in an arithmetic expression, we will solve them the first.
- O - stands for Of. It is basically Multiplication, but higher in hierarchy than Division.
- D - stands for Division (left-to-right) and M - stands for Multiplication (left-to-right)
- A - stands for Addition (left-to-right) and S - stands for Subtraction (left-to-right)
So, the word “BODMAS” works as a mnemonic and helps us remember this order.
Division and Multiplication are considered equal in hierarchy. We just solve them from left to right in a given expression.
For example, 12 ÷ 6 x 3 = (12 ÷ 6) x 3 = 2 x 3 = 6
And 12 x 6 ÷ 3 = (12 x 6) ÷ 3 = 72 ÷ 3 = 24
Similarly, Addition and Subtraction are considered equal in hierarchy. We just solve them from left to right in a given expression.
In fact, while solving you may also consider the minus sign to be the part of the number, i.e. we just add numbers, some of them may be positive and some negative.
For example, 2 + 3 - 4 = 2 + 3 + (-4) = 5 + (-4) = 1
Let’s see a few examples.
Q. Simplify the expression given below:
3 + 4 x 5
Explanation:
There are two operators in the given expression: addition and multiplication.
As per BODMAS rule, multiplication takes priority over addition. So, we will solve for it first.
3 + 4 x 5 = 3 + 20 = 23
(Not 3 + 4 x 5 = 7 x 5 = 35 … Wrong Answer)
Q. Simplify the expression given below:
12 ÷ 4 x 5
Explanation:
There are two operators in the given expression: division and multiplication.
As per BODMAS rule, division and multiplication are equal in hierarchy. So, we will just solve from left to right.
12 ÷ 4 x 5 = (12 ÷ 4) x 5 = 3 x 5 = 15
(Not 12 ÷ 4 x 5 = 12 ÷ 20 = 3/5 = 0.6 … Wrong Answer)
Q. Simplify the expression given below:
6 - 11 + 2
Explanation:
There are two operators in the given expression: addition and subtraction.
If we apply the BODMAS rule incorrectly, by assuming that addition takes priority over subtraction. Then, we will solve for it first.
6 - 11 + 2 = 6 - 13 = -7 (Wrong Answer)
But why?
What did we do wrong?
Afterall we followed the BODMAS rule. Let’s see.
As per BODMAS rule, addition and subtraction have the same hierarchy. We just need to solve them from left to right. So, 6 - 11 + 2 = (6 - 11) + 2 = -5 + 2 = -3 (Correct Answer)
We can also read the given expression as follows:
6 - 11 + 2 = (+6) + (-11) + (+2) = (+8) + (-11) = -3 (Correct Answer)
Types of Brackets
Now, we already know that brackets should be solved first of all in any given arithmetic expression. But there are four types of brackets, and they have their own hierarchy too.
- Vinculum - represented by a bar on the top of the numbers. E.g. $\overline{2 + 3}$. It has the highest hierarchy.
- Simple Bracket - represented by ( ). Second in hierarchy of brackets.
- Curly Bracket - represented by { }. Thord in hierarchy of brackets.
- Square Bracket - represented by [ ]. Fourth in hierarchy of brackets.
Q. Simplify the expression given below:
[6 - {5 + (4 + $\overline{2 + 3}$) - 1} - 2]
Explanation:
This expression has to be opened from inside outwards. So, we will simplify it as follows:
[6 - {5 + (4 + $\overline{2 + 3}$) - 1} + 2] = [6 - {5 + (4 + 5) - 1} - 2] (solved Vinculum first)
= [6 - {5 + 9 - 1} - 2] (solved Simple Bracket second)
= [6 - 13 - 2] (solved Curly Bracket third)
= -9 (solved Square Bracket at the last)
You should improve your calculation, if you want to get better in this chapter. For this purpose you should:
- Learn faster ways to do multiplication, division, etc.
- Learn faster ways to find squares, cubes, and roots.
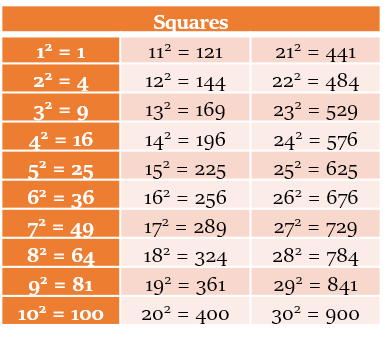
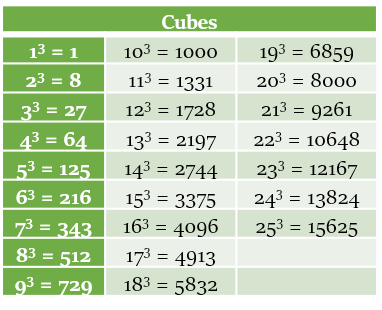
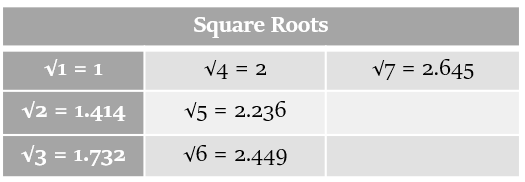
- Get familiar with frequently occurring numbers: Learn squares till 30, cubes till 12, square roots till 7, tables till 20 and maybe some log values too (e.g. log 2, log 3, log 5).
A few tables have been given below for your reference:
Percentage-based Simplification
Q. Simplify the expression given below:
20% of $\frac{2}{3}$ of 60
Explanation:
$\frac{2}{3}$ of 60 = $\frac{2}{3}$ × 60 = 40
20% of 40 = 8
The above example was simple. But sometimes we may have to face some tricky calculations. In that case, we have some tricks up our sleeves. Let’s see them using some examples.
Percentage Trick 1: Divide and Rule
We can divide the number or percentage in the given expression. It may ease out our calculation immensely.
32.5% of 50 = (30% + 2.5%) of 50 = 30% of 50 + 2.5% of 50
= 15 + 2% of 50 + 0.5% of 50
= 15 + 1 + 0.25 = 16.25
30% of 44 = 30% of (40 + 4) = 30% of 40 + 30% of 4
= 12 + 1.2 = 13.2
Percentage Trick 2: Common percentage method
It is somewhat similar to the trick mentioned above. Here, we take out a common percentage from the given two or more expressions, and thus reduce the percentage values that we need to do calculations on.
Q. 27% of 250 + 22% of 350 + 21% of 400 = ?
(a) 230 (b) 236.5 (c) 218.5 (d) 228.5
Explanation:
Here, we can take out 20% as common from all the given expressions.
27% of 250 + 22% of 350 + 21% of 400 = 20% of (250 + 350 + 400) + 7% of 250 + 2% of 350 + 1% of 400
= 20% of 1000 + 17.5 + 7 + 4 = 200 + 28.5 = 228.5
Answer: (d)
Percentage Trick 3: Swap
We can swap the number and percentage without changing the value of the expression.
That is, x% of y = y% of x
22% of 50 = 50% of 22 = 11
Percentage Trick 4: Fraction Conversion
There are some percentages that can easily be converted into fractions. This helps us a lot with some very complex looking percentage values.
83.33% of 24 = 8.333% of 240
= $\frac{1}{12}$ × 240 = 20
Digit-based Simplification
For some simple addition/subtraction/multiplication expressions we can simply make use of the digits based tricks to find the correct answer, or eliminate the wrong answers.
There are a few rules that we need to understand.
Digit sum rule
Digit sum of a given number is the sum of all its digits. Its value is always between 0 and 9.
For example, digit sum of 12345 = 1 + 2 + 3 + 4 + 5 = 15 = 1 + 5 = 6
In finding the digit-sum of a number, we can ignore the digit 9 or the digits that add up to 9.
For example, while finding the digit-sum of the number 196385, we can ignore the digits 9 and (1 + 8) & (6 + 3). So, the digit-sum of 196385 = 5
We can double-check it.
196385 = 1 + 9 + 6 + 3 + 8 + 5 = 32 = 3 + 2 = 5
Q. 3468 + 1258 – 596 – x = 3321 + 962
(a) 866 (b) 874 (c) 827 (d) 846
Explanation:
We will use the digit sum method to eliminate the wrong options.
(4 + 8) + (2 + 5) – (5 + 6) - x = (3 + 3 + 2 + 1) + (6 + 2)
or 12 + 7 – 11 - x = 9 + 8
or (1 + 2) + 7 – (1 + 1) - x = 0 + 8
or 3 + 7 – 2 – x = 8
or 8 - x = 8
or x = 0
Now, digit sum of only option (d) is 0: 8 + 4 + 6 = 18 = 1 + 8 = 9 = 0.
So, answer will be 846.
Answer: (d)
Q. What is the product of 129 and 35?
(a) 4510 (b) 4505 (c) 4515 (d) 4415
Explanation:
We will use the digit sum method to eliminate the wrong options.
Digit sum of 129 = 1 + 2 + 9 = 12 = 1 + 2 = 3 and
Digit sum of 35 = 3 + 5 = 8
Product of the digit sums = 3 × 8 = 24 = 2 + 4 = 6
Now, digit sum of only option (c) is 6: 4 + 5 + 1 + 5 = 15 = 1 + 5 = 6.
So, answer will be 4515.
Answer: (c)
Q. 88% of 370 + 24% of 210 – x = 118
(a) 268 (b) 258 (c) 246 (d) 356
Explanation:
We will use the digit sum method to eliminate the wrong options.
88% of 370 + 24% of 210 – x = 118
or $\frac{88}{100}$ × 370 + $\frac{24}{100}$ × 210 - x = 118
or (8 + 8) × (3 + 7 + 0) + (2 + 4) × (2 + 1 + 0) - x = (1 + 1 + 8)
or 16 × 10 + 6 × 3 - x = 10
or (1 + 6) × (1 + 0) + 18 - x = 1 + 0
or 7 × 1 + (1 + 8) - x = 1
or 7 + 9 - x = 1
or 7 + 0 - x = 1
or x = 6
Now, digit sum of only option (b) is 6: 2 + 5 + 8 = 15 = 1 + 5 = 6.
So, answer will be 258.
Answer: (b)
Unit digit rule
If digit sum of two or more options is same, then we will use unit digit rule to eliminate the rest of the options.
In unit digit rule, we just focus on unit digits of the numbers (i.e. only the last digit), and ignore the rest.
Q. 4368 + 2158 – 596 – x = 3421 + 1262
(a) 1066 (b) 1274 (c) 1247 (d) 1384
Explanation:
We will use the digit sum method to eliminate the wrong options.
(4 + 8) + (2 + 5) – (5 + 6) - x = (3 + 4 + 2 + 1) + (1 + 2 + 6 + 2)
or 12 + 7 – 11 - x = 10 + 11
or (1 + 2) + 7 – (1 + 1) - x = (1 + 0) + (1 + 1)
or 3 + 7 – 2 – x = 1 + 2
or 8 - x = 3
or x = 5
Now, digit sum of option (b) is 5: 1 + 2 + 7 + 4 = 14 = 1 + 4 = 5.
Now, digit sum of option (c) is also 5: 1 + 2 + 4 + 7 = 14 = 1 + 4 = 5.
So, options (b) and (c) have the same digit sum as x.
So, we will solve this by using unit digit rule.
8 + 8 – 6 – x = 1 + 2
or x = 8 + 8 - 6 - 3
or x = 16 – 9 = 7
Now, unit digit of only option (c) is 7.
So, answer will be 1247.
Answer: (c)
Tens digit rule
If unit digit is also same, then we will use tens digit rule.
In tens digit rule, we just focus on unit and tens digits of the numbers (i.e. only the last two digits), and ignore the rest.
Q. 7960 + 2956 – 8050 + 4028 = x
(a) 6984 (b) 6884 (c) 6894 (d) 5884
Explanation:
We will use the digit sum method to eliminate the wrong options.
(7 + 6) + (2 + 5 + 6) – (8 + 5) + (4 + 2 + 8) = x
or 13 + 13 - 13 + 14 = x
or (1 + 3) + (1 + 4) = x
or x = 4 + 5 = 9 = 0
Now, digit sum of option (a) is 0: 6 + 9 + 8 + 4 = 27 = 2 + 7 = 9 = 0.
Now, digit sum of option (c) is also 0: 6 + 8 + 9 + 4 = 27 = 2 + 7 = 9 = 0.
So, options (a) and (c) have the same digit sum as x.
Now, let’s try to solve this by using unit digit rule.
0 + 6 - 0 + 8 = x
or x = 14 = 4 (we will just focus on the unit digit)
Unit digit of option (a): 4
Unit digit of option (c): 4
So, in options (a) and (c) digit sum & unit digit are same. So, now we will go for tens digit rule.
60 + 56 – 50 + 28 = x
or x = 94
Tens digit of option (a): 8
Tens digit of option (c): 9
Hence, option (c) is the correct answer.
Answer: (c)
Indices-based Simplification
Some simplification questions are based on indices/powers, e.g. squares, cubes, square roots, cube roots etc.
Q. $21^2 + 17^2 – 11^2$ = ?
(a) 609 (b) 509 (c) 615 (d) 719
Explanation:
= 441 + 28 × 6 = 441 + 168 = 609
Answer: (a)
Q. $13^{36} × 13^{-18} = 169^2$ × ?
(a) $13^{15}$ (b) $13^{11}$ (c) $13^{12}$ (d) $13^{14}$
Explanation:
$13^{36} × 13^{-18} = 169^2$ × ?
or $13^{36} × 13^{-18} = (13^2)^2$ × ?
or $13^{36} × 13^{-18} = 13^4$ × ?
or ? = $\frac{13^{36} × 13^{-18}}{13^4}$ = $13^{36 - 18 - 4}$ = $13^{14}$
Answer: (d)
Algebra-based Simplification
Some simplification questions can be solved by directly applying some algebric formulae. We may also use these algebric formulae to find certain powers of numbers, and even ease-out some multiplications for us.
We recommend you to refer to our Algebra module, and learn the basic algebric formulae from there. Here, we will focus more on the application part.
Trick 1: $(x + y)^2 \hspace{1ex} and \hspace{1ex} (x – y)^2$
We know that:
$(x + y)^2 = x^2 + y^2 + 2xy = (x – y)^2 + 4xy$
$(x – y)^2 = x^2 + y^2 – 2xy = (x + y)^2 - 4xy$
So, $108^2 = (100 + 8)^2 = 100^2 + 8^2 + (2 × 100 × 8) \hspace{1ex} \hspace{1ex} [as \hspace{1ex} (x + y)^2 = x^2 + y^2 + 2xy]$
= 10000 + 64 + 1600 = 11,664
Similarly, $92^2 = (100 - 8)^2 = 100^2 + 8^2 - (2 × 100 × 8) \hspace{1ex} \hspace{1ex} [as \hspace{1ex} (x - y)^2 = x^2 + y^2 - 2xy]$
= 10000 + 64 - 1600 = 8,464
Q. Simplify the expression given below:
51 × 51 + 42 × 42 + 2 × 51 × 42
Explanation:
We know that: $(x + y)^2 = x^2 + y^2 + 2xy$
So, 51 × 51 + 42 × 42 + 2 × 51 × 42 = $(51 + 42)^2$ = $93^2$
Q. Simplify the expression given below:
51 × 51 + 49 × 49
Explanation:
We know that: $(x + y)^2 = x^2 + y^2 + 2xy$ and $(x – y)^2 = x^2 + y^2 – 2xy$
So, $(x + y)^2 + (x – y)^2 = 2 (x^2 + y^2)$
So, 51 × 51 + 49 × 49 = $(50 + 1)^2 + (50 - 1)^2 = 2 (50^2 + 1^2)$ = 2 (2500 + 1) = 2 × 2501 = 5002
Trick 2: $x^2 – y^2 = (x + y)(x – y)$
We know that:
$x^2 – y^2 = (x + y)(x – y)$
So, 18 × 22 = (20 - 2) × (20 + 2) = $20^2 - 2^2 \hspace{1ex} \hspace{1ex} [as \hspace{1ex} x^2 – y^2 = (x + y)(x – y)]$
= 400 - 4 = 396
Trick 3: $(x + y)^3 \hspace{1ex} and \hspace{1ex} (x – y)^3$
We know that:
$(x + y)^3 = x^3 + y^3 + 3xy (x + y)$
$(x – y)^3 = x^3 – y^3 – 3xy(x – y)$
Q. Simplify the expression given below:
$1.7^3 + 1.3^3 + 3 × 1.7 × 1.3 (1.7 + 1.3)$
Explanation:
We know that: $(x + y)^3 = x^3 + y^3 + 3xy (x + y)$
So, $1.7^3 + 1.3^3 + 3 × 1.7 × 1.3 (1.7 + 1.3) = (1.7 + 1.3)^3 = 3^3 = 27$
Trick 4: $x^3 + y^3 \hspace{1ex} and \hspace{1ex} x^3 - y^3$
We know that:
$x^3 + y^3 = (x + y) (x^2 + y^2 – xy) = (x + y)^3 – 3xy (x + y)$
$x^3 – y^3 = (x – y) (x^2 + y^2 + xy) = (x – y)^3 + 3xy (x – y)$
Q. Simplify the expression given below:
$\frac{108 × 108 × 108 \hspace{1ex} - \hspace{1ex} 18 × 18 × 18}{108 × 108 \hspace{1ex} + \hspace{1ex} 108 × 18 \hspace{1ex} + \hspace{1ex} 18 × 18}$
Explanation:
We know that: $x^3 – y^3 = (x – y) (x^2 + y^2 + xy)$
or $\frac{x^3 – y^3}{x^2 + y^2 + xy}$ = x - y
Here, x = 108 and y = 18
So, $\frac{108 × 108 × 108 \hspace{1ex} - \hspace{1ex} 18 × 18 × 18}{108 × 108 \hspace{1ex} + \hspace{1ex} 108 × 18 \hspace{1ex} + \hspace{1ex} 18 × 18}$ = 108 - 18 = 90
Approximation Trick
In all the above types of simplification methods, we can sometimes use approximation trick to ease out our calculation.
We can do so because in objective aptitude examinations, we are not supposed to find the exact answer, rather we just need to select the correct option. If the options are not very close, then we can definitely use this trick.
Q. $\frac{3805.99}{380.6} × \sqrt{485} × 1.5001$ = 11 × ?
(a) 33 (b) 30 (c) 27 (d) 35
Explanation:
$\frac{3805.99}{380.6} × \sqrt{485} × 1.5001$ = 11 × ?
We can take approximate values and ease out our calculation. As options are not very close, we still should be able to recognize the right option, even if we do not get the exact answer.
So, the above equation can be rewritten as follows, without having much impact on the values of the various expressions.
$\frac{3800}{380} × 22 × 1.5$ = 11 × ? ($22^2$ = 484)
or 10 × 22 × 1.5 = 11 × ?
or ? = 30
Answer: (b)