Finding Square roots and Cube roots
What is Evolution in Maths?
Evolution is the process of finding the roots of an expression/number.
Root is a quantity, which when multiplied by itself one, two, three …. n times, produces the given expression/number.
For example, square root, cube root etc.
Even and Odd roots
If to get the given expression/number, we have to multiply the root by itself even number of times, then it is called an even root, e.g. square root.
For example, $\sqrt{3} × \sqrt{3}$ = 3 (root has to be multiplied 2 times)
Only positive quantities can have an even root (not negative quantities). An even root may be positive or negative.
If to get the given expression/number, we have to multiply the root by itself odd number of times, then it is called an odd root, e.g. cube root.
For example, $\sqrt[3]{2} × \sqrt[3]{2} × \sqrt[3]{2}$ = 2 (root has to be multiplied 3 times)
Any quantity can have an odd root (i.e. both positive and negative quantities). An odd root may be positive or negative; it will have the same sign as that of the quantity.
Square Root
If square root of an expression/number x is r, then we can write it as:
- r = $\sqrt{x}$, or
- x = $r^2$
Every positive real number has two square roots:
- positive square root (or principal square root), e.g. $\sqrt{9}$ = 3
- negative square root, e.g. $\sqrt{9}$ = -3
So, in general, we write the square root of a positive real number with a preceding ± sign. For example, $\sqrt{9}$ = ±3
Negative real numbers also have two square roots. Fo example, square roots of -9 are 3i and -3i, where i = $\sqrt{-1}$
How to find Square Root of a number?
Let’s learn how to find square roots of various kinds of numbers. We have divided the numbers in two categories for this purpose:
- Perfect Square Numbers, e.g. 25, 36 etc.
- Other Numbers
We can utilize multiple methods to find square root of a number. Let’s learn a few of them.
Using Square Root Division Method
We can use this method to find the square roots of any number (perfect squares or not). Let’s understand the steps involved in this method using an example.
Let’s find out the square root of 29,320.
Step 1: We will divide the dividend (i.e. 29,320) in a group of two digits, starting from the units digit, i.e. from the right hand side. If the number of digits are odd (as is the case with 29,320), then the extreme left block will have only one digit. So, our dividend will look like this:
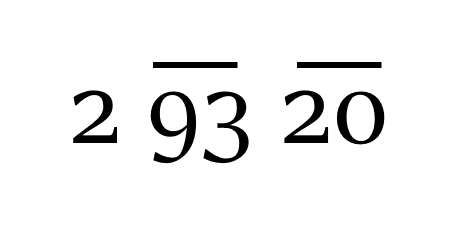
In case we were finding the square root of a decimal number, say 29320.348, then the process of making blocks of two numbers will start from the decimal point, to the left, as well as to the right.
On the right side, we can always add a 0 to make a pair of digits, without changing the value of the given number.
So, our dividend will look like this:
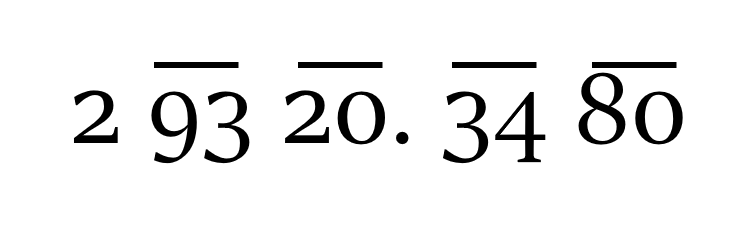
Step 2: So, we know the dividend. But what about divisor?
In Square Root Division Method we have to drive our divisor in each step. That is, it will keep on changing.
For the first step of our calculation, we will consider the leftmost block of digits in our dividend, i.e. 2. Our divisor for this step will be the integral part of the square root of 2. We know that 2 falls between 1 and 4. So, it’s square root must be 1.something. It’s integral part is 1, which will be our first divisor.
We will write this in place of the divisor, and also on top of the horizontal line as quotient. It has been shown in the figure below:
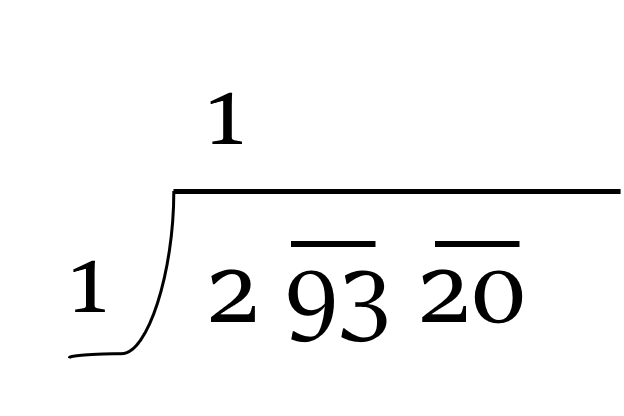
Step 3: Now, multiply this number with itslf, and subtract it from the leftmost block of numbers.
So, we get 2 - (1 × 1) = 2 - 1 = 1
Thereafter, bring down the next block of two digits to get the new dividend, 193.
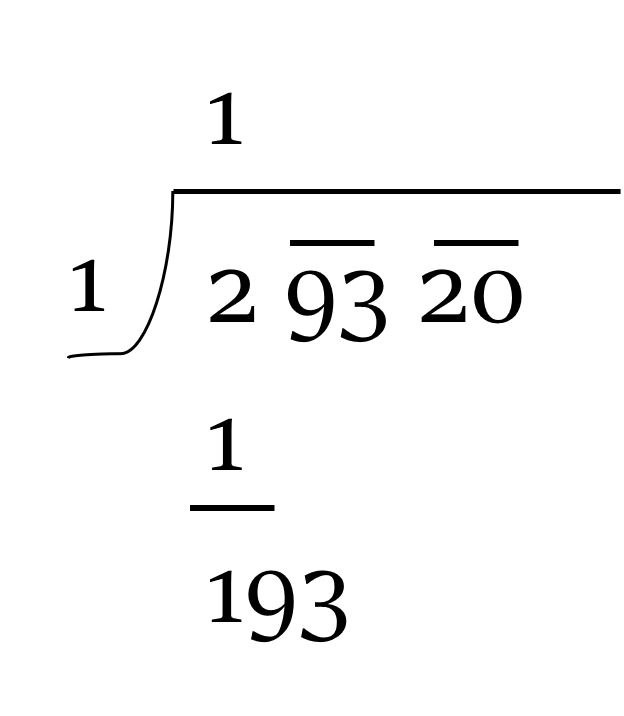
Step 4: So, we know the new dividend. But what about the new divisor?
The new divisor will have two parts:
- The first part can be drived by adding the divisor of the last step to its unit digit. In our case, it will be 1 (last divisor) + 1 (unit digit of last divisor) = 2
- Let the second part of the divisor be x. So, our new divisor will be 2x. Now, find such a value of the digit x, such that (2x) × x is the greatest possible number that is less than or equal to the new dividend.
In our case, if we put x = 7, then 27 × 7 = 189 (which is less than 193); while 28 × 8 = 224 (which is more than 193). So, our new divisor is 27. We will place this new value of x (i.e. 7) at the top of the horizontal bar too.
Now, substract this product from the dividend, i.e. 193 - 189 = 4
Thereafter, bring down the next block of two digits to get the new dividend, 420.
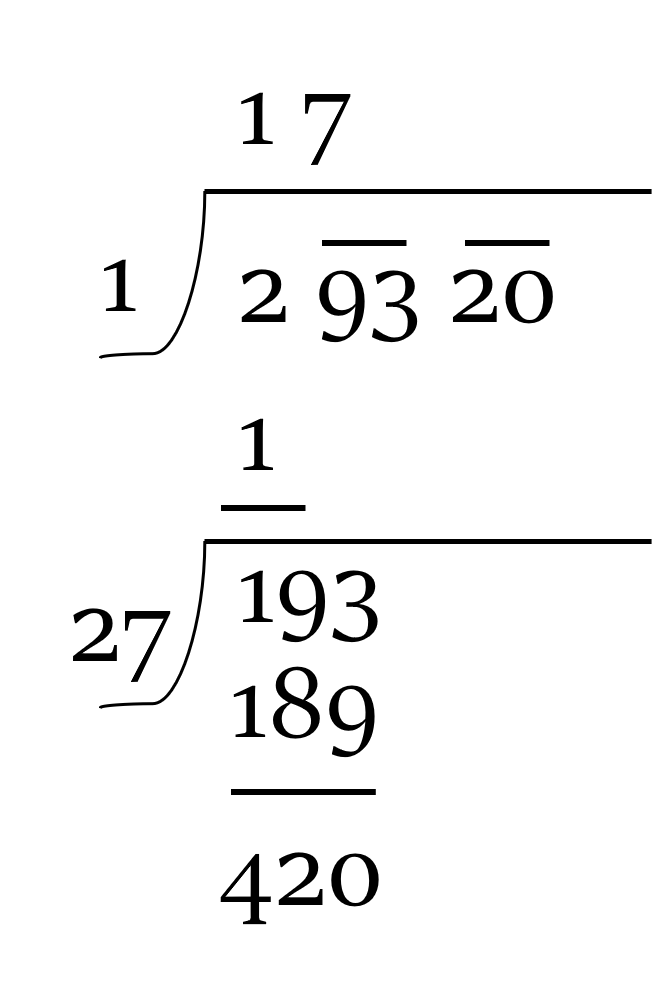
Step 5: So, we know the new dividend. But what about the new divisor?
The process that we followed in the above step should be followed again.
The new divisor will have two parts:
- The first part can be drived by adding the divisor of the last step to its unit digit. In our case, it will be 27 (last divisor) + 7 (unit digit of last divisor) = 34
- Let the second part of the divisor be x. So, our new divisor will be 34x. Now, find such a value of the digit x, such that (34x) × x is the greatest possible number that is less than or equal to the new dividend.
In our case, if we put x = 1, then 341 × 1 = 341 (which is less than 420); while 342 × 2 = 684 (which is more than 420). So, our new divisor is 341. We will place this new value of x (i.e. 1) at the top of the horizontal bar too.
Now, substract this product from the dividend, i.e. 420 - 341 = 79
If our number 29,320 would have been a perfect square, then we would have got 0 as remainder in this step. That is, in case of perfect squares, when there will be no more digits left to be brought down, we will get a remainder of 0.
However, as we got a remainder here, it means that our required square root must have a decimal component.
Thereafter, bring down the next block of two digits to get the new dividend. As, no numbers are left, we will put a decimal point in the quotient, and add two zeroes to 79 to get the new dividend, 7900.
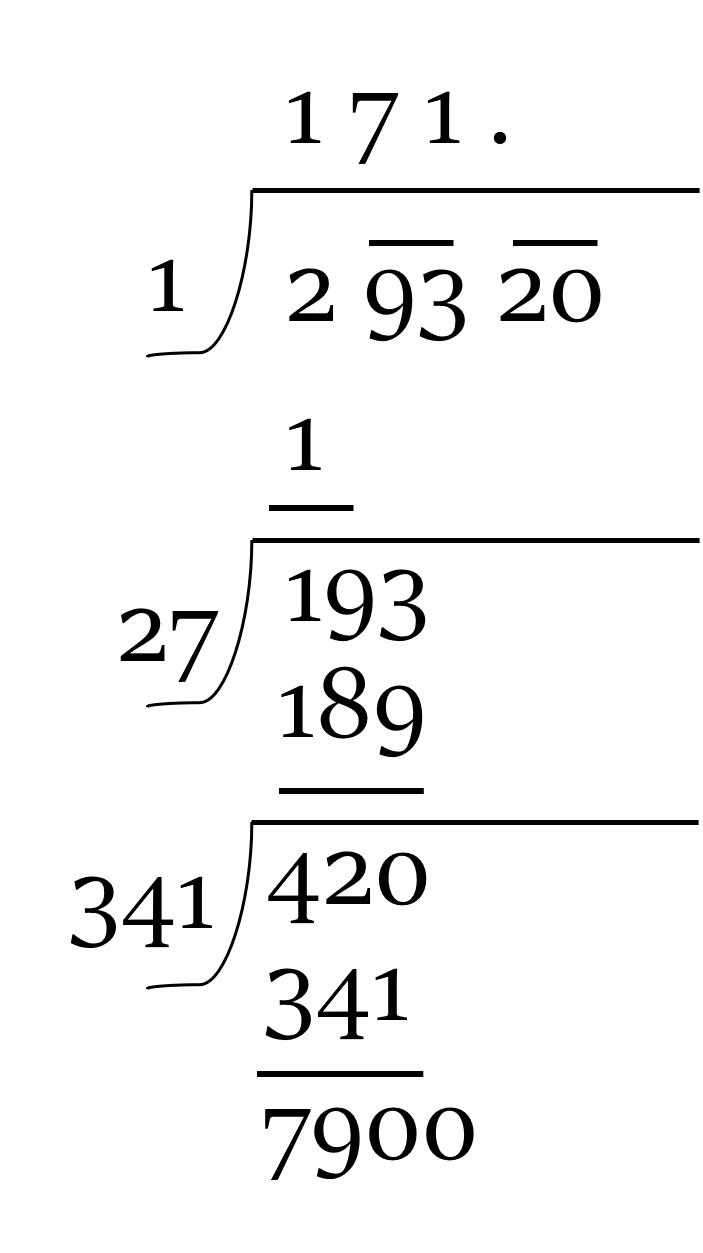
Step 6: So, we know the new dividend. But what about the new divisor?
The process that we followed in the above step should be followed again.
The new divisor will have two parts:
- The first part can be drived by adding the divisor of the last step to its unit digit. In our case, it will be 341 (last divisor) + 1 (unit digit of last divisor) = 342
- Let the second part of the divisor be x. So, our new divisor will be 342x. Now, find such a value of the digit x, such that (342x) × x is the greatest possible number that is less than or equal to the new dividend.
In our case, if we put x = 2, then 3422 × 2 = 6844 (which is less than 7900); while 3423 × 3 = 10269 (which is more than 7900). So, our new divisor is 3422. We will place this new value of x (i.e. 2) at the top of the horizontal bar too.
Now, substract this product from the dividend, i.e. 7900 - 6844 = 1056
Thereafter, add two zeroes to 1056 to get the new dividend, 105600.
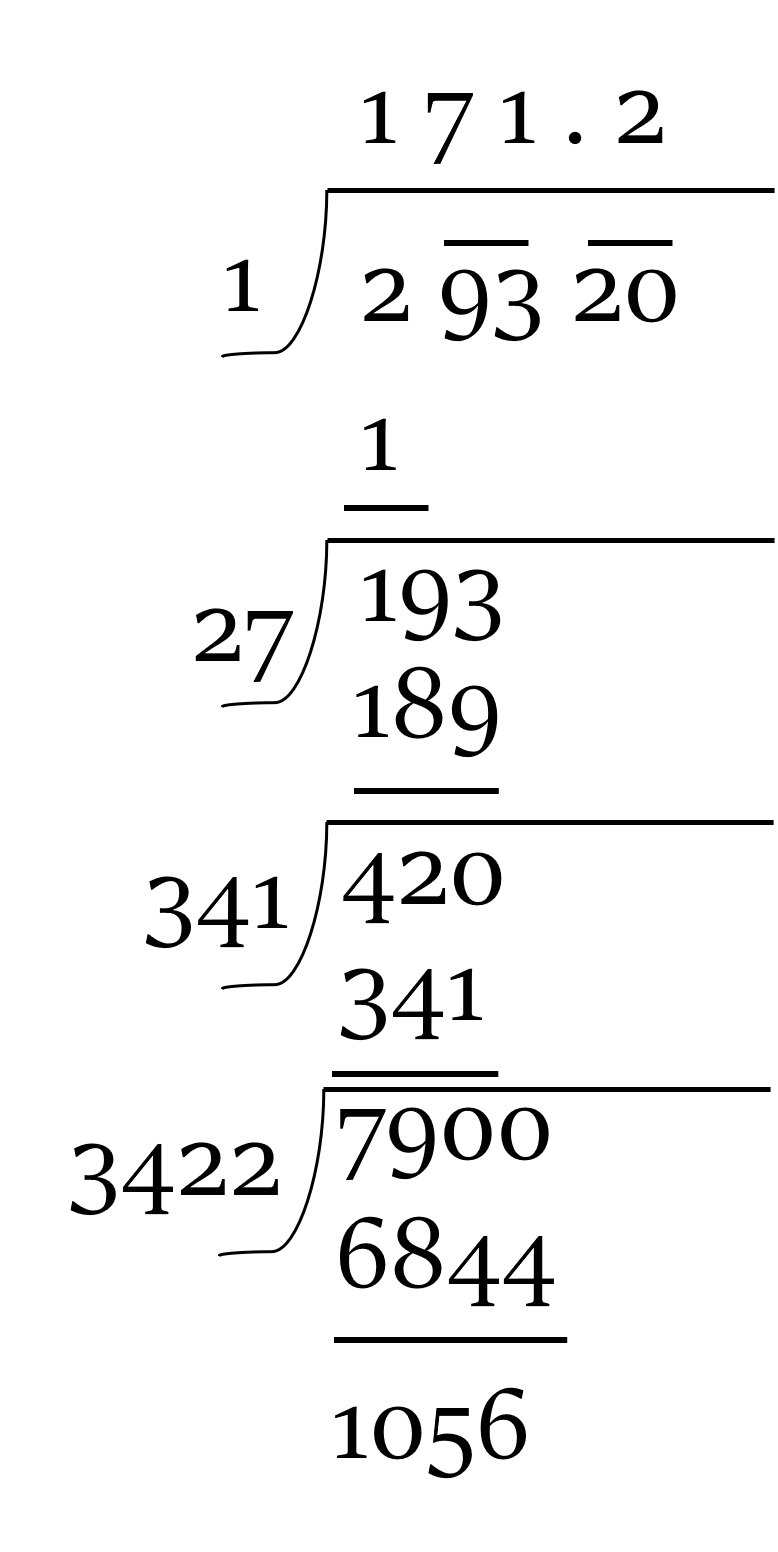
Hit and Try Method
Make a rough estimate of the square root of a number, and check if your estimate is true by multiplying that number by itself. Make adequate corrections if the resulting number is less/more than the given number.
This method works fine for smaller numbers. Let’s see a few examples.
Say, we have to find the square root of 529. Now, we already know that $20^2$ = 400, and $25^2$ = 625. So, the required number must be more than 20, but less than 25. 529 seems closer to 625 than 400. So, our required root must be closer to 25 than 20. Let’s check $23^2$ - it’s value is 529. Bingo!
We can also use the above method to find approximate square root values of numbers that are not perfect squares.
Solve in Parts Method
In this method, we divide the given number in parts and then find out its square root. We use this method to find the square roots of perfect squares. So, this method has limited applicability. In most cases, we don’t know whether the given number is a perfect square or not.
But it can still be useful in some cases, because it’s very fast and may even help us find approximate values of the square roots of numbers that are not perfect squares.
In this method, we make use of the knowledge regarding the last digit of squares. Have a look at the table given below:

You will notice that the last digit of a square depends on the last digit of the number being squared.
For example, $6^2$ = 36, $16^2$ = 256, $1236^2$ = 1527696 (all squares have the same last digit 6)
$3^2$ = 9, $13^2$ = 169, $1233^2$ = 1520289 (all squares have the same last digit 9)
Now, let’s understand the method. We follow the following steps:
- Step 1: Divide the number in two parts: two rightmost digits and the rest of the number. For example, 144 can be written as $1 \overline{44}$; 5476 can be written as $\overline{54}$ $\overline{76}$; 11664 can be written as $\overline{116}$ $\overline{64}$.
- Step 2: Ignore the rightmost pair of digits, i.e. the last set. Focus on the rest of the number, i.e. the first part, e.g. in $1 \overline{44}$, ignore 44.
- Step 3: Find the maximum possible number, whose square is less than or equal to the first part, i.e. 1. This will be the first digit(s) of our required square root. $1^2$ = 1 (= 1). So, the first digit of the answer is 1.
- Step 4: The last digit of the square root will depend on the last digit of the given number, i.e. on 4. You may refer the table given above to find the last digit of the square root. So, the last digit of the answer must be either 2 or 8.
- Step 5: If there are more than one possible digits (in our case 2 or 8), we will multiply the first part of the answer we got in Step 3 and (left part answer + 1), i.e. 1 × (1 + 1) = 1 × 2 = 3. If it comes out to be greater than the left part of the given number, then the right part of the answer will be smaller of the two. Otherwise, if it comes out to be lesser than the left part of the given number, then the right part of the answer will be greater of the two. In our case, 3 > 1. So, the right part of the answer will be smaller of 2 and 8, i.e. 2. So, our square root will be 12.
Was that too much? Don’t worry. It will become clear once you go through a few examples.
So, without further ado, let’s go ahead and see a few examples.
Q. Find the square root of 1225.
Explanation:
- Step 1: 1225 can be written as $\overline{12}$ $\overline{25}$.
- Step 2; Ignore 25 and focus on 12.
- Step 3: We know that $3^2$ = 9 (< 12). So, first digit of our square root will be 3.
- Step 4: Last digit of 1225 is 5. As per the table, the square of a number can end with digit 5 only if the last digit of that number is 5. So, the last digit of our square root must be 5.
So, $\sqrt{1225}$ = 35
Q. Find the square root of 3249.
Explanation:
- Step 1: 3249 can be written as $\overline{32}$ $\overline{49}$.
- Step 2; Ignore 49 and focus on 32.
- Step 3: We know that $5^2$ = 25 (< 32). So, first digit of our square root will be 5.
- Step 4: Last digit of 3249 is 9. As per the table, the square of a number can end with digit 9 only if the last digit of that number is 3 or 7. So, the last digit of our square root must be 3 or 7. But which one?
- Step 5: We found out in Step 3, that the first digit of our square root must be 5. Now, 5 × 6 = 30. It is less than the first part of the given number, i.e. 30 < 32. So, the last digit of the required square root must be greater of 3 and 7, i.e. 7.
So, $\sqrt{3249}$ = 57
Q. Find the square root of 24336.
Explanation:
- Step 1: 24336 can be written as $\overline{243}$ $\overline{36}$.
- Step 2; Ignore 36 and focus on 243.
- Step 3: We know that $15^2$ = 225 (< 243). So, first digit of our square root will be 15.
- Step 4: Last digit of 24336 is 6. As per the table, the square of a number can end with digit 6 only if the last digit of that number is 4 or 6. So, the last digit of our square root must be 4 or 6. But which one?
- Step 5: We found out in Step 3, that the first digit of our square root must be 15. Now, 15 × 16 = 240. It is less than the first part of the given number, i.e. 240 < 243. So, the last digit of the required square root must be greater of 4 and 6, i.e. 6.
So, $\sqrt{3249}$ = 156
Cube Root
If cube root of an expression/number x is r, then we can write it as:
- r = $\sqrt[3]{x}$, or
- x = $r^3$
Every real number (positive or negative) has three cube roots:
- one real cube root, e.g. $\sqrt[3]{27}$ = 3 (because $3^3$ = 27), and $\sqrt[3]{-27}$ = -3 (because $-3^3$ = -27)
- two complex cube roots, e.g. apart from the real cube root 1, the number 1 has two complex cube roots too → $(-\frac{1}{2} + i\frac{\sqrt{3}}{2})$ and $(-\frac{1}{2} - i\frac{\sqrt{3}}{2})$
How to find Cube Root of a number?
Solve in Parts Method
We used this method to find out square roots earlier in this article. We can also use it to find cube roots.
In this method, we divide the given number in parts and then find out its cube root. We use this method to find the cube roots of perfect cubes. So, this method has limited applicability. In most cases, we don’t know whether the given number is a perfect cube or not.
But it can still be useful in some cases, because it’s very fast and may even help us find approximate values of the cube roots of numbers that are not perfect cubes.
In this method, we make use of the knowledge regarding the last digit of cubes. Have a look at the table given below:

You will notice that the last digit of a cube depends on the last digit of the number being cubed.
For example, $6^3$ = 216, $16^3$ = 4096, $1236^3$ = 1,88,82,32,256 (all cubes have the same last digit 6)
$3^3$ = 27, $13^3$ = 2197, $1233^3$ = 1,87,45,16,337 (all cubes have the same last digit 7)
Now, let’s understand the method. We follow the following steps:
- Step 1: Divide the number in two parts: three rightmost digits and the rest of the number. For example, 1728 can be written as $1 \overline{728}$; 35937 can be written as $\overline{35}$ $\overline{937}$.
- Step 2: Ignore the rightmost set of digits, i.e. the last set. Focus on the rest of the number, i.e. the first part, e.g. in $1 \overline{728}$, ignore 728.
- Step 3: Find the maximum possible number, whose cube is less than or equal to the first part, i.e. 1. This will be the first digit(s) of our required cube root. $1^3$ = 1 (= 1). So, the first digit of the answer is 1.
- Step 4: The last digit of the cube root will depend on the last digit of the given number, i.e. on 8. You may refer the table given above to find the last digit of the square root. So, the last digit of the answer must be 2. So, our cube root will be 12.
It will become clear once you go through a few examples.
Q. Find the cube root of 32768.
Explanation:
- Step 1: 32768 can be written as $\overline{32}$ $\overline{768}$.
- Step 2; Ignore 768 and focus on 32.
- Step 3: We know that $3^3$ = 27 (< 32). So, first digit of our square root will be 3.
- Step 4: Last digit of 32768 is 8. As per the table, the cube of a number can end with digit 8 only if the last digit of that number is 2. So, the last digit of our cube root must be 2.
So, $\sqrt{32768}$ = 32