Definite Integrals

Till now we have been dealing with indefinite integrals. In this article, we will understand the concept of definite integrals.

Definite vs Indefinite Integrals

We already know that, we can use the process of Integration to find the area between the curve of a function and the x-axis.

In this process, we divide the area to be calculated into rectangular slices. Then we calculate the area of each of these rectangular slices and add them up.

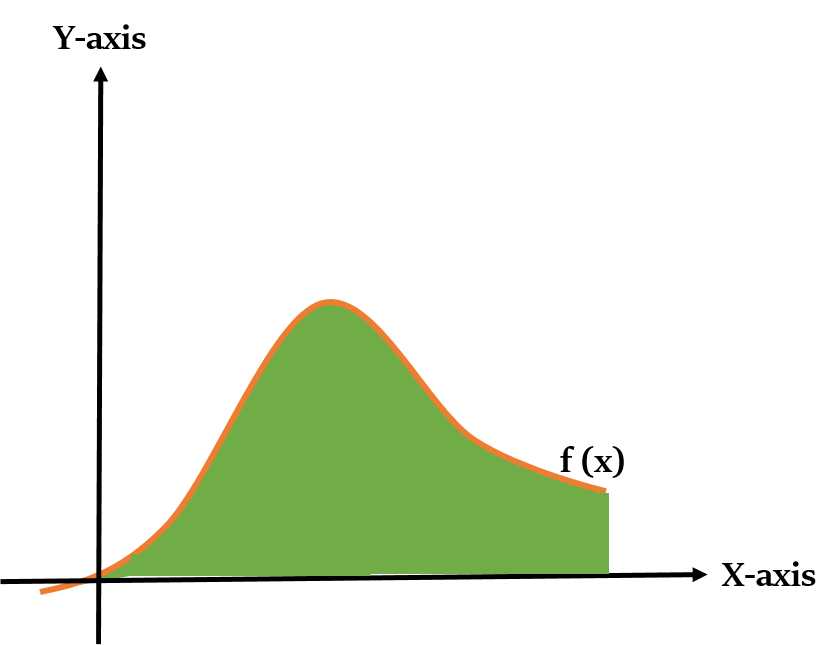
This is Indefinite Integral, as we are not setting any limits on the x-axis (i.e. the limits are indefinite). So, here the whole area between the curve and the x-axis is being calculated. It is just denoted by ∫ symbol, i.e. ∫ f(x) dx.

However, in Definite Integral we set the limits on the x-axis (i.e. the limits are definite). Only the area between these limits will be calculated. 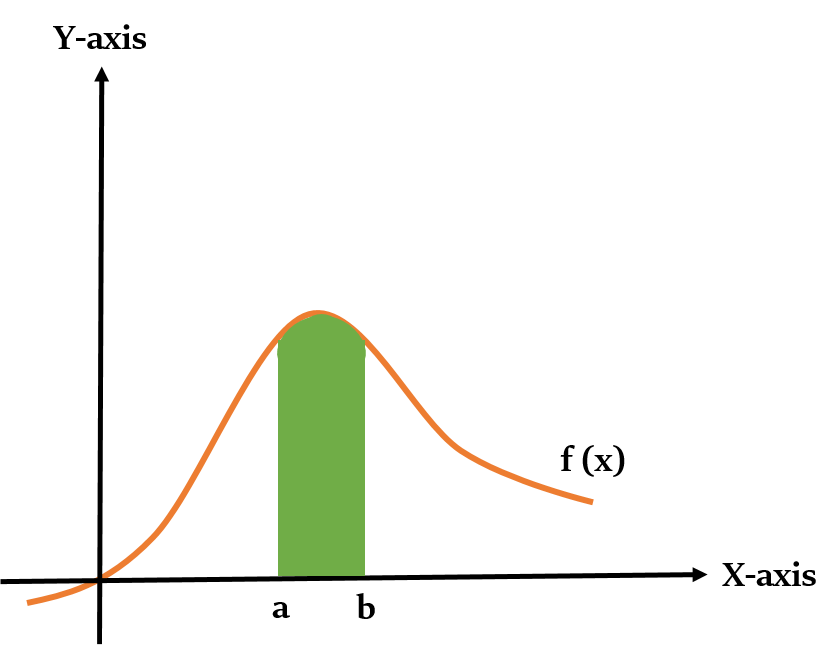It is just denoted by $\int_{a}^{b}$ symbol. The upper limit is placed at the top of ∫, and the lower limit is placed at the bottom of ∫, i.e. $\int_{a}^{b} f(x)$ dx.

It basically means that we find the area of the curve till x = b, and then subtract the area of the curve till x = a.

So, Definite integral between a and b = Indefinite integral at b - Indefinite integral at a

Let’s see an example.

We know that, ∫ 2x dx = $x^2$ + c

This is indefinite integral.

Now, if we have to find definite integral with limits of a = 2 and b = 3, then we will represent it as follows:
$\int_{2}^{3} 2x$ dx = $[x^2]^3_2$
= $3^2 - 2^2$ = 9 - 4 = 5

Properties of Definite Integral

Property 1: Zero length interval

If the upper and lower limits of a definite integral are the same, i.e. a = b, then the result will always be zero.

$\int_{a}^{a} f(x)$ dx = 0

Property 2: Adding intervals

We can break the interval in multiple parts, and calculate the value of definite integral over those parts separately, and then add them up. It will give us the same result as the definite integral over the whole interval.

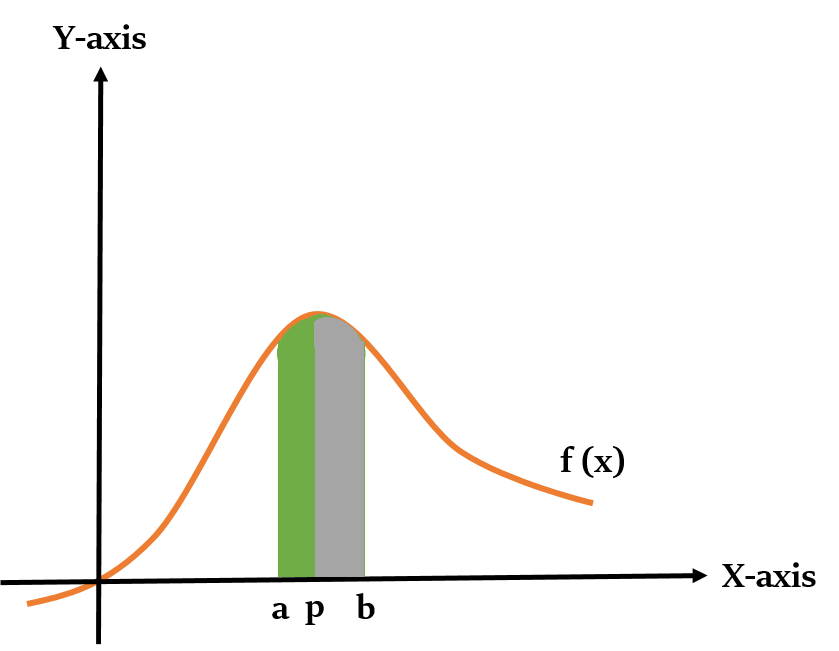
$\int_{a}^{b} f(x)$ dx = $\int_{a}^{p} f(x)$ dx + $\int_{p}^{b} f(x)$ dx

Property 3: Reversing Limits

If we reverse the limits of a definite integral, then we will get the same answer but with opposite sign.

$\int_{a}^{b} f(x)$ dx = - $\int_{b}^{a} f(x)$ dx

Property 4: Addition of Functions

We can find integrals of two functions (say f and g) separately, and then add them up later. It will give us the same result as the integral of f + g.

$\int_{a}^{b} [f(x) + g(x)]$ dx = $\int_{a}^{b} f(x)$ dx + $\int_{a}^{b} g(x)$ dx

Property 5: Net Area

Through definite integral we calculate the net area between a curve and the x-axis. The area above the x-axis is considered positive, and the area below the x-axis is considered negative.

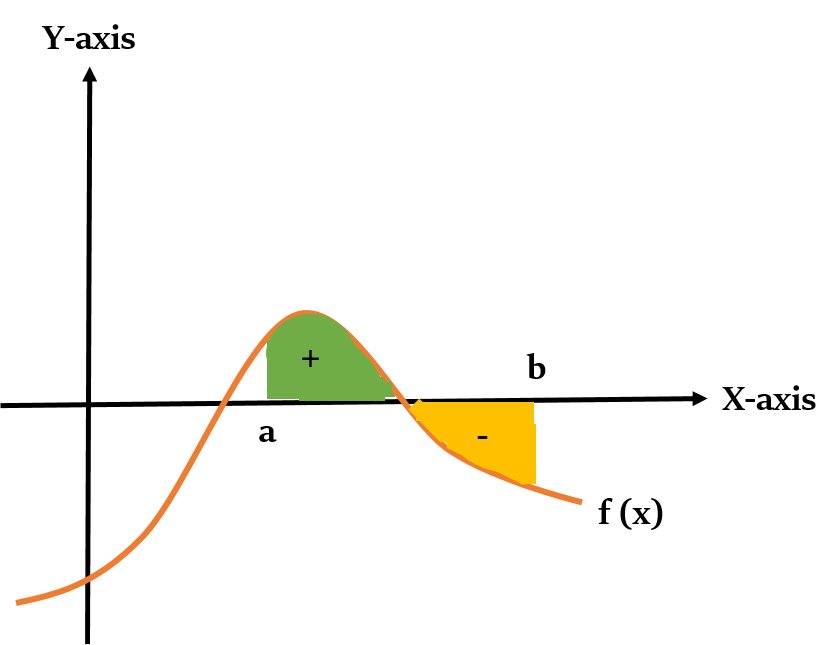
So, net area = Area above x-axis - Area below x-axis

If area above x-axis is more, then the net area that we will calculate using definite integration will come out to be positive. If the area below x-axis is more, then net area will come out to be negative.

If we just want to find the total area, irrespective of whether it’s above or below the x-axis, then we should find out these areas separately, and then add them.